-
See Also
- Graph
- GraphPlot3D
- LayeredGraphPlot
- TreePlot
- CommunityGraphPlot
- GraphLayout
- GraphEmbedding
-
- Entity Types
- Graph
-
- Interpreter Types
- Graph
- ComputedGraph
-
- Formats
- Graphlet
- DOT
- GraphML
- Related Guides
-
-
See Also
- Graph
- GraphPlot3D
- LayeredGraphPlot
- TreePlot
- CommunityGraphPlot
- GraphLayout
- GraphEmbedding
-
- Entity Types
- Graph
-
- Interpreter Types
- Graph
- ComputedGraph
-
- Formats
- Graphlet
- DOT
- GraphML
- Related Guides
-
See Also
GraphPlot[g]
generates a plot of the graph g.
GraphPlot[{e1,e2,…}]
generates a plot of the graph with edges ei.
GraphPlot[{…,w[ei],…}]
plots ei with features defined by the symbolic wrapper w.
GraphPlot[{vi 1vj 1,…}]
uses rules vikvjk to specify the graph g.
GraphPlot[m]
uses the adjacency matrix m to specify the graph g.


GraphPlot
GraphPlot[g]
generates a plot of the graph g.
GraphPlot[{e1,e2,…}]
generates a plot of the graph with edges ei.
GraphPlot[{…,w[ei],…}]
plots ei with features defined by the symbolic wrapper w.
GraphPlot[{vi 1vj 1,…}]
uses rules vikvjk to specify the graph g.
GraphPlot[m]
uses the adjacency matrix m to specify the graph g.
Details and Options
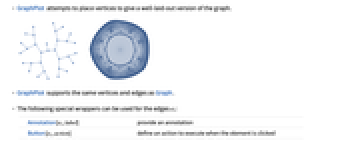




- GraphPlot attempts to place vertices to give a well-laid-out version of the graph.
- GraphPlot supports the same vertices and edges as Graph.
- The following special wrappers can be used for the edges ei:
-
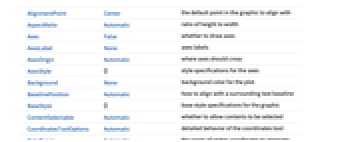
Annotation[ei,label] provide an annotation Button[ei,action] define an action to execute when the element is clicked EventHandler[ei,…] define a general event handler for the element Hyperlink[ei,uri] make the element act as a hyperlink Labeled[ei,…] display the element with labeling PopupWindow[ei,cont] attach a popup window to the element StatusArea[ei,label] display in the status area when the element is moused over Style[ei,opts] show the element using the specified styles Tooltip[ei,label] attach an arbitrary tooltip to the element - GraphPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
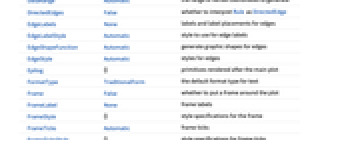
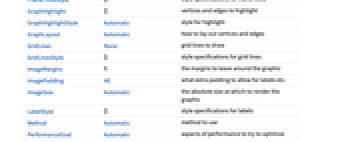
DataRange Automatic the range of vertex coordinates to generate DirectedEdges False whether to interpret Rule as DirectedEdge EdgeLabels None labels and label placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic styles for edges GraphLayout Automatic how to lay out vertices and edges GraphHighlight {} vertices and edges to highlight GraphHighlightStyle Automatic style for highlight Method Automatic method to use PerformanceGoal Automatic aspects of performance to try to optimize PlotStyle Automatic graphics directives to determine styles PlotTheme Automatic overall theme for the graph VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and label placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Automatic size of vertices VertexStyle Automatic styles for vertices - With the setting VertexCoordinates->Automatic, the embedding of vertices and routing of edges is computed automatically, based on the setting for GraphLayout.
- Possible special embeddings for GraphLayout include:
-

"BipartiteEmbedding" vertices on two parallel lines 
"CircularEmbedding" vertices on a circle 
"CircularMultipartiteEmbedding" vertices on segments of a circle 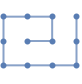
"DiscreteSpiralEmbedding" vertices on a discrete spiral 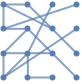
"GridEmbedding" vertices on a grid 
"LinearEmbedding" vertices on a line 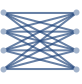
"MultipartiteEmbedding" vertices on several parallel lines 
"SpiralEmbedding" vertices on a 3D spiral projected to 2D 
"StarEmbedding" vertices on a circle with a center - Possible structured embeddings for layered graphs such as trees and directed acyclic graphs include:
-

"BalloonEmbedding" vertices on a circle with the center at the parent vertex 
"RadialEmbedding" vertices on a circular segment 
"LayeredDigraphEmbedding" vertices on parallel lines for directed acyclic graphs 
"LayeredEmbedding" vertices on parallel lines - Possible optimizing embeddings all minimize a quantity and include:
-
"HighDimensionalEmbedding" energy for spring-electrical in high dimension 
"PlanarEmbedding" number of edge crossings 
"SpectralEmbedding" weighted sum of squares distances 
"SpringElectricalEmbedding" energy with edges as springs and vertices as charges 
"SpringEmbedding" energy with edges as springs 
"TutteEmbedding" number of edge crossings and distance to neighbors - Possible settings for PlotTheme include common base themes:
-
"Business" a bright, modern look appropriate for business presentations or infographics 
"Detailed" identify data by employing labels and tooltips 
"Marketing" elegant, eye-catching design suitable for marketing needs 
"Minimal" simple graph 
"Monochrome" single-color design 
"Scientific" candid design useful for analyzing detailed data with labels and tooltips 
"Web" clean, bold design suitable for a consumer website or blog 
"Classic" historical design of graph to remain compatible with existing uses - Graph features themes affect plot of vertices and edges. Feature themes include:
-
"LargeGraph" large graph 
"ClassicLabeled" classic graph 
"IndexLabeled" index-labeled graph -
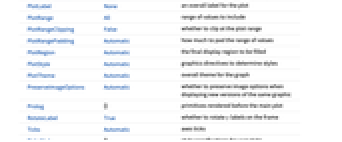
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DataRange Automatic the range of vertex coordinates to generate DirectedEdges False whether to interpret Rule as DirectedEdge EdgeLabels None labels and label placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic styles for edges Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GraphHighlight {} vertices and edges to highlight GraphHighlightStyle Automatic style for highlight GraphLayout Automatic how to lay out vertices and edges GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Method Automatic method to use PerformanceGoal Automatic aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to determine styles PlotTheme Automatic overall theme for the graph PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and label placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Automatic size of vertices VertexStyle Automatic styles for vertices
List of all options



Examples
open all close allBasic Examples (3)
Scope (11)
Graph Specification (6)
Specify a graph using a graph:
Specify a graph using a rule list:
Specify a graph using a dense adjacency matrix:
Specify a graph using a sparse adjacency matrix:
Use GraphData for collections of graphs:
Use ExampleData for collections of sparse matrices:
Options (71)
GraphLayout (66)
"BalloonEmbedding" (6)
Place each vertex in an enclosing circle centered at its parent vertex:
"BalloonEmbedding" works best for tree graphs:
Use the option "EvenAngle"->True to place vertices evenly in an enclosing circle:
With the setting "OptimalOrder"->True, the vertex ordering optimizes the angular resolution and the aspect ratio:
"CircularEmbedding" (2)
"CircularMultipartiteEmbedding" (2)
"DiscreteSpiralEmbedding" (3)
"GridEmbedding" (2)
"HighDimensionalEmbedding" (2)
"LayeredEmbedding" (6)
Place vertices in several layers in such a way as to minimize edges between nonadjacent layers:
"LayeredEmbedding" works best for tree graphs:
Use the option "LayerSizeFunction"->func to specify the relative height:
Use the option "RootVertex"->v to set the root vertex:
Use the option "LeafDistance"->d to specify the leaf distance:
Use the option "Orientation"->o to draw a tree with different orientations:
"LayeredDigraphEmbedding" (3)
"LinearEmbedding" (2)
"MultipartiteEmbedding" (2)
"RadialEmbedding" (2)
"SpectralEmbedding" (2)
"SpiralEmbedding" (2)
"SpringElectricalEmbedding" (12)
Place vertices so that they minimize mechanical and electrical energy when each vertex has a charge and each edge corresponds to a spring:
With the setting "EdgeWeighted"->True, edge weights are used:
Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:
Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:
Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:
Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:
With the setting "Octree"->True, an octree data structure (in three dimensions) or a quadtree data structure (in two dimensions) is used in the calculation of repulsive force:
Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:
Use "RepulsiveForcePower"->r to control how fast the repulsive force decays over distance:
Use "StepControl"->method to define how step length is modified during energy minimization:
Use "StepLength"->r to specify the initial step length used in moving the vertices around:
Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:
"SpringEmbedding" (10)
Place vertices so that they minimize mechanical energy when each edge corresponds to a spring:
With the setting "EdgeWeighted"->True, edge weights are used:
Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:
Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:
Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:
Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:
Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:
Use "StepControl"->method to define how step length is modified during energy minimization:
Use "StepLength"->r to specify the initial step length used in moving the vertices around:
Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:
"StarEmbedding" (3)
PlotStyle (3)
Specify an overall style for the graph:
PlotStyle can be combined with VertexShapeFunction, which has higher priority:
PlotStyle can be combined with EdgeShapeFunction, which has higher priority:
Applications (27)
Basic Applications (3)
Graph Theory (5)
Linguistic or Geographic Data (3)
Number Properties (11)
Numbers that have a common divisor:
Numbers that have no common divisor:
Link a number to another with a 1 bit inserted:
Link a number to another with a 0 bit inserted:
Link a number to another with 1 bit deleted:
Link a number to another that is one bit different:
Link a number to another that is one bit reversed:
Link a number to another that is one bit rotated right:
Link a number to another that is one bit rotated left:
Sparse Test Matrices (3)
A sparse test matrix related to a structure from NASA's Langley Research Center:
A sparse test matrix related to a finite element model of a geodesic dome:
Use ArrayPlot or MatrixPlot to display sparse matrices:
Properties & Relations (8)
Use LayeredGraphPlot for hierarchical-style drawing of directed graphs:
Use TreePlot for different types of tree drawing:
Use GraphPlot3D to draw graphs in 3D:
Use GraphData for an extensive collection of predefined graphs and properties:
Get the connectivity and plot it:
Use VertexCoordinates to use the embedding provided by GraphData:
Use PolyhedronData for a large collection of polyhedra and properties:
Compare to a predefined embedding:
Use ExampleData for a large collection of sparse matrices:
Use GeoGraphValuePlot to show the values on geographic networks:
Use GeoGraphPlot to plot relationships between geographic locations on a map:
See Also
Graph GraphPlot3D LayeredGraphPlot TreePlot CommunityGraphPlot GraphLayout GraphEmbedding
Entity Types: Graph
Interpreter Types: Graph ComputedGraph
Function Repository: SimpleHypergraphPlot
Related Guides
Text
Wolfram Research (2007), GraphPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphPlot.html (updated 2019).
CMS
Wolfram Language. 2007. "GraphPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/GraphPlot.html.
APA
Wolfram Language. (2007). GraphPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphPlot.html
BibTeX
@misc{reference.wolfram_2025_graphplot, author="Wolfram Research", title="{GraphPlot}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/GraphPlot.html}", note=[Accessed: 07-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphplot, organization={Wolfram Research}, title={GraphPlot}, year={2019}, url={https://reference.wolfram.com/language/ref/GraphPlot.html}, note=[Accessed: 07-January-2026]}