PRODUCTS
PURCHASE
FOR USERS
COMPANY
OUR SITES
DOCUMENTATION CENTER SEARCH
Mathematica
>
Gamma Functions and Related Functions
>
Built-in
Mathematica
Symbol
Special Functions
Tutorials »
|
Beta
BetaRegularized
InverseGammaRegularized
InverseErf
See Also »
|
Functions Used in Statistics
Gamma Functions and Related Functions
Inverse Functions
More About »
InverseBetaRegularized
InverseBetaRegularized
[
s
,
a
,
b
]
gives the inverse of the regularized incomplete beta function.
MORE INFORMATION
Mathematical function, suitable for both symbolic and numerical manipulation.
With the regularized incomplete beta function defined by
,
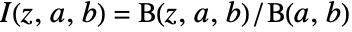InverseBetaRegularized
[
s
,
a
,
b
]
is the solution for
z
in
.
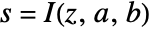InverseBetaRegularized
[
z
0
,
s
,
a
,
b
]
gives the inverse of
BetaRegularized
[
z
0
,
z
,
a
,
b
]
.
Note that the arguments of
InverseBetaRegularized
are arranged differently than in
InverseGammaRegularized
.
For certain special arguments,
InverseBetaRegularized
automatically evaluates to exact values.
InverseBetaRegularized
can be evaluated to arbitrary numerical precision.
InverseBetaRegularized
automatically threads over lists.
EXAMPLES
CLOSE ALL
Basic Examples
(2)
Evaluate numerically:
In[1]:=
Out[1]=
In[1]:=
Out[1]=
Scope
(4)
Generalizations & Extensions
(2)
Applications
(1)
Properties & Relations
(2)
Possible Issues
(2)
SEE ALSO
Beta
BetaRegularized
InverseGammaRegularized
InverseErf
TUTORIALS
Special Functions
RELATED LINKS
MathWorld
The Wolfram Functions Site
MORE ABOUT
Functions Used in Statistics
Gamma Functions and Related Functions
Inverse Functions
New in 3
© 2008 Wolfram Research, Inc.
, InverseBetaRegularized[s, a, b] is the solution for z in 
.
EXAMPLES
Basic Examples 
Scope 