- See Also
-
Related Guides
- Logic & Boolean Algebra
- Boolean Computation
- Computational Geometry
- Supervised Machine Learning
- Text Analysis
- Natural Language Processing
- Sequence Alignment & Comparison
- Distance and Similarity Measures
- Date & Time
- Machine Learning
- Scientific Models
- Linguistic Data
- Math & Counting Operations on Lists
- Computer Vision
- Audio Analysis
- Audio Processing
- Speech Computation
- Tech Notes
-
- See Also
-
Related Guides
- Logic & Boolean Algebra
- Boolean Computation
- Computational Geometry
- Supervised Machine Learning
- Text Analysis
- Natural Language Processing
- Sequence Alignment & Comparison
- Distance and Similarity Measures
- Date & Time
- Machine Learning
- Scientific Models
- Linguistic Data
- Math & Counting Operations on Lists
- Computer Vision
- Audio Analysis
- Audio Processing
- Speech Computation
- Tech Notes
Nearest[{elem1,elem2,…},x]
gives the list of elemi to which x is nearest.
Nearest[{elem1v1,elem2v2,…},x]
gives the vi corresponding to the elemi to which x is nearest.
Nearest[{elem1,elem2,…}{v1,v2,…},x]
gives the same result.
Nearest[{elem1,elem2,…}prop,x]
gives the property prop for the elemi to which x is nearest.
Nearest[data,{x1,x2,…}]
effectively gives {Nearest[data,x1],Nearest[data,x2],…}.
Nearest[data,x,n]
gives the n nearest elemi to x.
Nearest[data,x,{n,r}]
gives the n or fewer nearest elemi to x that are within radius r of x.
Nearest[data]
generates a NearestFunction[…] that can be applied repeatedly to different x.


Nearest
Nearest[{elem1,elem2,…},x]
gives the list of elemi to which x is nearest.
Nearest[{elem1v1,elem2v2,…},x]
gives the vi corresponding to the elemi to which x is nearest.
Nearest[{elem1,elem2,…}{v1,v2,…},x]
gives the same result.
Nearest[{elem1,elem2,…}prop,x]
gives the property prop for the elemi to which x is nearest.
Nearest[data,{x1,x2,…}]
effectively gives {Nearest[data,x1],Nearest[data,x2],…}.
Nearest[data,x,n]
gives the n nearest elemi to x.
Nearest[data,x,{n,r}]
gives the n or fewer nearest elemi to x that are within radius r of x.
Nearest[data]
generates a NearestFunction[…] that can be applied repeatedly to different x.
Details and Options



- Nearest works for a variety of data, including numerical, geospatial, textual, and visual, as well as dates and times.
- The data can also be given as an association. In this case, Nearest[<|key1val1,key2val2,…|>] is equivalent to Nearest[{val1key1,val2key2,…}].
- In Nearest[{elem1,elem2,…}prop,…], possible forms for prop include:
-
"Element" the elemi found to be nearest "Index" the index i of the elemi found to be nearest "Distance" the distance to the nearest elemi {prop1,prop2,…} a list of multiple forms All an association giving element, index and distance - When Nearest returns several elements elemi, the nearest ones are given first.
- If several elements are at the same distance, they are returned in the order they appear in data.
- Nearest[data,x,{All,r}] can be used to get all elemi within radius r.
- The following options can be given:
-
DistanceFunction Automatic the distance metric to use Method Automatic method to use WorkingPrecision Automatic precision to use for numeric data - By default, the following distance functions are used for different types of elemi:
-
Norm[#1-#2]& numeric data JaccardDissimilarity Boolean data EditDistance strings ColorDistance colors ImageDistance images DateDifference dates and times GeoDistance geospatial data - Nearest with geospatial data uses GeoDistance to compute distances. The data can be given as a list of GeoPosition objects, or a GeoPosition containing an array of points.
- For images or colors and a distance function f, DistanceFunction->f is passed to ImageDistance and ColorDistance, respectively. »
- All images are conformed using ConformImages. With DistanceFunction->Automatic, dimensionality reduction based on discrete cosine transform is applied to the set of images.
- Using Norm[#1-#2,p]& for
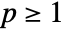 or named distance functions such as ManhattanDistance, ChessboardDistance, and EuclideanDistance can invoke special optimizations for numeric vector data.
or named distance functions such as ManhattanDistance, ChessboardDistance, and EuclideanDistance can invoke special optimizations for numeric vector data. - Possible settings for Method include "Octree", "KDtree", and "Scan".
- Possible settings for the WorkingPrecision option are:
-
MachinePrecision use machine-precision numbers p use precision p Automatic use adaptive precision to resolve nearest points
Examples
open all close allBasic Examples (5)
Scope (9)
Give the elements within radius 2:
Give at most 3 nearest elements within radius 2:
Find which element is nearest to {2,3} in 2D and return the appropriate label:
Compute the same using an Association:
Return the index for the nearest string:
Return an Association giving the string element, index, and distance:
Find the 3 elements nearest to 20, simultaneously reporting the elements and their distance to 20:
For uniform random points in 3D, give the distances for the 10 nearest to the origin:
For each of the 10 nearest, give an Association including the point element, index and distance:
Create a lookup function for future use:
Find the date nearest to a given DateObject:
Find out which of these {lat,lon} points on Earth is closest to you:
Express the input as a list of separate GeoPosition objects instead:
Report simultaneously the closest point and the distance to it:
Options (6)
DistanceFunction (3)
By default, normal Euclidean distance is used for points:
Use the ManhattanDistance, which sums the length of each side:
The ChessboardDistance only takes into account the dimension with the largest separation:
The DistanceFunction can be given as a symbol:
Find nearest colors using a color distance different from the default distance in ColorDistance:
Method (2)
Compare different methods for machine-precision data:
In three dimensions, the "KDtree" method is faster:
In 20 dimensions, a simple scan is faster:
The setting Method->{"KDtree","LeafSize"->s} may be used to control the maximum number of points in any leaf of the KD tree constructed:
WorkingPrecision (1)
Using WorkingPrecision->MachinePrecision ensures the fastest evaluation method is used:
The results may not be correct if the numbers are not all distinct to machine precision:
All the points are effectively the same to machine precision:
Applications (8)
Plot the Nearest of a list of:
Use a 1-norm ("taxicab distance"):
Highlight the 200 random points closest to the origin:
Create a nearest function from all the words in a dictionary:
Look up words closest to a given word:
Find the outputs from running a sequence of elementary cellular automata:
Generate a complete list of outputs from all 256 elementary cellular automata:
Find which rules give outputs nearest the specified sequences:
Use a negative distance function to find the element farthest away from the given element:
Show the returned element for all values between 1 and 5:
Compute the nearest of the points of that polygon from your current geo location:
Properties & Relations (2)
In the case of a tie, all nearest elements are returned in order:
The single argument form of Nearest returns a NearestFunction object:
This is an optimized lookup function, which is faster than calling Nearest repeatedly:
Tech Notes
Related Guides
-
▪
- Logic & Boolean Algebra ▪
- Boolean Computation ▪
- Computational Geometry ▪
- Supervised Machine Learning ▪
- Text Analysis ▪
- Natural Language Processing ▪
- Sequence Alignment & Comparison ▪
- Distance and Similarity Measures ▪
- Date & Time ▪
- Machine Learning ▪
- Scientific Models ▪
- Linguistic Data ▪
- Math & Counting Operations on Lists ▪
- Computer Vision ▪
- Audio Analysis ▪
- Audio Processing ▪
- Speech Computation
History
Introduced in 2007 (6.0) | Updated in 2014 (10.0) ▪ 2016 (11.0) ▪ 2017 (11.1)
Text
Wolfram Research (2007), Nearest, Wolfram Language function, https://reference.wolfram.com/language/ref/Nearest.html (updated 2017).
CMS
Wolfram Language. 2007. "Nearest." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Nearest.html.
APA
Wolfram Language. (2007). Nearest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Nearest.html
BibTeX
@misc{reference.wolfram_2025_nearest, author="Wolfram Research", title="{Nearest}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/Nearest.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_nearest, organization={Wolfram Research}, title={Nearest}, year={2017}, url={https://reference.wolfram.com/language/ref/Nearest.html}, note=[Accessed: 24-February-2026]}