Interpolation

Interpolation[{f1,f2,…}]

constructs an interpolation of the function values fi, assumed to correspond to x values 1, 2, … .

Interpolation[{{x1,f1},{x2,f2},…}]

constructs an interpolation of the function values fi corresponding to x values xi.

Interpolation[{{{x1,y1,…},f1},{{x2,y2,…},f2},…}]

constructs an interpolation of multidimensional data.

Interpolation[{{{x1,…},f1,df1,…},…}]

constructs an interpolation that reproduces derivatives as well as function values.

Interpolation[data,x]

find an interpolation of data at the point x.

Details and Options

  • Interpolation returns an InterpolatingFunction object, which can be used like any other pure function.
  • The interpolating function returned by Interpolation[data] is set up so as to agree with data at every point explicitly specified in data.
  • The function values fi can be real or complex numbers, or arbitrary symbolic expressions.
  • The fi can be lists or arrays of any dimension.
  • The function arguments xi, yi, etc. must be real numbers.
  • Different elements in the data can have different numbers of derivatives specified.
  • For multidimensional data, the n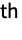^(th) derivative can be given as a tensor with a structure corresponding to D[f,{{x,y,…},n}].
  • Partial derivatives not specified explicitly can be given as Automatic.
  • Interpolation works by fitting polynomial curves between successive data points.
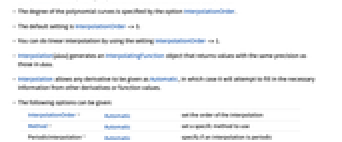
  • The degree of the polynomial curves is specified by the option InterpolationOrder.
  • The default setting is InterpolationOrder->3.
  • You can do linear interpolation by using the setting InterpolationOrder->1.
  • Interpolation[data] generates an InterpolatingFunction object that returns values with the same precision as those in data.
  • Interpolation allows any derivative to be given as Automatic, in which case it will attempt to fill in the necessary information from other derivatives or function values.
  • The following options can be given:
  • InterpolationOrder Automaticset the order of the interpolation
    Method Automaticset a specifc method to use
    PeriodicInterpolation Automaticspecify if an interpolation is periodic
  • Interpolation supports a Method option. Possible settings include "Spline" for spline interpolation and "Hermite" for Hermite interpolation.

Examples

open allclose all

Basic Examples  (2)

Construct an approximate function that interpolates the data:

Apply the function to find interpolated values:

Plot the interpolation function:

Compare with the original data:

Find the interpolated value immediately:

Scope  (4)

Interpolate between points at arbitrary values:

Create data with Table:

Form the interpolation:

Plot the interpolated function:

Create a list of multidimensional data:

Create an approximate interpolating function:

Plot the interpolating function:

Form an interpolation from data given as a TimeSeries:

Plot the interpolated function:

Generalizations & Extensions  (5)

Create data that includes derivatives at each point:

Construct an interpolation:

Plot the interpolation:

Create 2D data that includes a gradient vector at each point:

Compare with data that does not include gradients:

Also include tensors of second derivatives:

Create a vector-valued InterpolatingFunction of one variable from vector-valued data:

The value is a vector:

Plot will show both components:

Create a vector-valued InterpolatingFunction of two variables from vector-valued data:

The value is a vector:

Plot3D will show all three components:

A single component may be plotted using Part:

Derivatives may also be included for Hermite interpolation:

Options  (5)

InterpolationOrder  (3)

Make a zeroth‐order interpolation:

Make a linear interpolation:

Make a quadratic interpolation:

Method  (1)

Compare splines with piecewise Hermite interpolation for random data:

The curves appear close, but the spline has a continuous derivative:

PeriodicInterpolation  (1)

Make an interpolating function that repeats periodically:

Applications  (2)

Interpolate random data:

Find a continuous interpolation of the GCD function:

Properties & Relations  (2)

The interpolating function always goes through the data points:

Find the integral of an interpolating function:

Plot the interpolating function and its integral:

Possible Issues  (3)

Extrapolation is attempted to go beyond the original data:

With the default choice of order, at least 4 points are needed in each dimension:

With a lower order, fewer points are needed:

The interpolation function will always be continuous, but may not be differentiable:

Neat Examples  (1)

Interpolate the sequence of primes:

Wolfram Research (1991), Interpolation, Wolfram Language function, https://reference.wolfram.com/language/ref/Interpolation.html (updated 2008).

Text

Wolfram Research (1991), Interpolation, Wolfram Language function, https://reference.wolfram.com/language/ref/Interpolation.html (updated 2008).

CMS

Wolfram Language. 1991. "Interpolation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Interpolation.html.

APA

Wolfram Language. (1991). Interpolation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Interpolation.html

BibTeX

@misc{reference.wolfram_2024_interpolation, author="Wolfram Research", title="{Interpolation}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Interpolation.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_interpolation, organization={Wolfram Research}, title={Interpolation}, year={2008}, url={https://reference.wolfram.com/language/ref/Interpolation.html}, note=[Accessed: 21-December-2024 ]}