Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

InterpolatingPolynomial

InterpolatingPolynomial[{f₁,f₂,…},x]

constructs an interpolating polynomial in x which reproduces the function values at successive integer values 1, 2, … of .

InterpolatingPolynomial[{{x₁,f₁},{x₂,f₂},…},x]

constructs an interpolating polynomial for the function values corresponding to values .

InterpolatingPolynomial[{{{x₁,y₁,…},f₁},{{x₂,y₂,…},f₂},…},{x,y,…}]

constructs a multidimensional interpolating polynomial in the variables x, y, ….

InterpolatingPolynomial[{{{x₁,…},f₁,df₁,…},…},{x,…}]

constructs an interpolating polynomial that reproduces derivatives as well as function values.

Details and Options

The function values 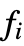and sample points 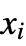, etc. can be arbitrary real or complex numbers, and in 1D can be arbitrary symbolic expressions.
With a 1D list of data of length 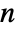, InterpolatingPolynomial gives a polynomial of degree .
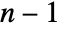With any given specified set of data, there are infinitely many possible interpolating polynomials; InterpolatingPolynomial always tries to find the one with lowest total degree.
InterpolatingPolynomial gives the interpolating polynomial in a Horner form, suitable for numerical evaluation.
Different elements in the data can have different numbers of derivatives specified.
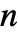
For multidimensional data, the 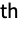derivative can be given as a tensor with a structure corresponding to D[f,{{x,y,…},n}]. »
InterpolatingPolynomial allows any function value or derivative to be given as Automatic, in which case it will attempt to fill in the necessary information from derivatives or other function values. »
The option setting Modulus->n specifies that the interpolating polynomial should be found modulo . »

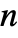Examples

open allclose all

Basic Examples (2)

Construct an interpolating polynomial for the squares:

Check the result:

Construct an interpolating polynomial through three points:

Check the result at a single point:

Scope (3)

Make the polynomial have derivative 0 when it has value 8:

Interpolate values depending on 2 variables:

Generalizations & Extensions (3)

Make the polynomial have zero derivative at and without specifying the values there:

Specify some of the partial derivatives in 2 dimensions:

Interpolate values and a gradient in 3 variables:

Options (1)

Modulus (1)

Find a polynomial interpolating the given points in arithmetic mod 47:

The polynomial takes on the specified values mod 47:

Applications (5)

Construct a polynomial with roots a, b, and c:

Newton–Cotes integration formulas with points:

Centered finite difference formula of order for approximating the first derivative:

Interpolate to find the characteristic polynomial of a matrix:

Create a tensor product interpolation:

Create an interpolating polynomial for each fixed value:

Show the interpolation curves in the direction:

Interpolate between the curves in the direction:

Show the interpolating surface and data points:

Properties & Relations (3)

The interpolating polynomial always goes through the data points:

ListInterpolation creates a tensor product interpolation:

Create a numerical InterpolatingFunction object:

Create a symbolic polynomial by interpolating in each dimension separately:

Verify that results agree with random data points:

Choose some points to be interpolated:

Use VandermondeMatrix in LinearSolve to obtain the coefficients of the interpolating polynomial:

Possible Issues (3)

Runge's function:

Sampling at evenly spaced intervals in the interval from to :

The polynomial that interpolates these points has large oscillations:

Interpolation uses a lower-order piecewise polynomial that does not have this problem:

When derivatives are specified without function values an interpolant may not be found:

There is no quadratic polynomial that satisfies the interpolation conditions:

Points with abscissas lying on a line in 2 dimensions:

In multiple dimensions an interpolant may not be found for some arrangements of points:

This polynomial interpolates the data above, but has total degree 2:

Top