Sqrt

Sqrt[z]

or gives the square root of z.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
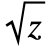  • can be entered using or ∖(∖@z∖).
  • Sqrt[z] is converted to .
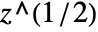  • Sqrt[z^2] is not automatically converted to z.
  • Sqrt[a b] is not automatically converted to Sqrt[a]Sqrt[b].
  • These conversions can be done using PowerExpand, but will typically be correct only for positive real arguments.
  • For certain special arguments, Sqrt automatically evaluates to exact values.
  • Sqrt can be evaluated to arbitrary numerical precision.
  • Sqrt automatically threads over lists. »
  • In StandardForm, Sqrt[z] is printed as .
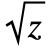  • √z can also be used for input. The √ character is entered as sqrt or \[Sqrt].

Examples

open allclose all

Basic Examples  (6)

Evaluate numerically:

Enter using :

Negative numbers have imaginary square roots:

Plot over a subset of the reals:

Plot over a subset of the complexes:

is not necessarily equal to :

It can be simplified to if one assumes :

Scope  (39)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Sqrt can deal with real‐valued intervals:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix Sqrt function using MatrixFunction:

Compute average-case statistical intervals using Around:

Specific Values  (4)

Values of Sqrt at fixed points:

Values at zero:

Values at infinity:

Find a value of for which using Solve:

Substitute in the result:

Visualize the result:

Visualization  (4)

Plot the real and imaginary parts of the Sqrt function:

Compare the real and imaginary parts of and (Surd[x,2]):

Plot the real part of :

Plot the imaginary part of :

Polar plot with :

Function Properties  (10)

The real domain of Sqrt:

It is defined for all complex values:

Sqrt achieves all non-negative values on the reals:

The range for complex values is the right half-plane, excluding the negative imaginary axis:

Find limits at branch cuts:

Enter a √ character as sqrt or \[Sqrt], followed by a number:

is not an analytic function:

Nor is it meromorphic:

is neither non-decreasing nor non-increasing:

However, it is increasing where it is real valued:

is injective:

Not surjective:

is non-negative on its domain of definition:

has a branch cut singularity for :

However, it is continuous at the origin:

is neither convex nor concave:

However, it is concave where it is real valued:

Differentiation  (3)

The first derivative with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z:

Formula for the ^(th) derivative with respect to z:

Integration  (3)

Compute the indefinite integral using Integrate:

Verify the anti-derivative:

Definite integral:

More integrals:

Series Expansions  (4)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

The general term in the series expansion using SeriesCoefficient:

The first-order Fourier series:

The Taylor expansion at a generic point:

Function Identities and Simplifications  (4)

Primary definition:

Connection with Exp and Log:

is not automatically replaced by :

It can be simplified to if one assumes :

It can be simplified to TemplateBox[{x}, Abs] if one assumes x in TemplateBox[{}, Reals]:

PowerExpand can be used to force cancellation without assumptions:

Expand assuming real variables x and y:

Applications  (4)

Roots of a quadratic polynomial:

Generate periodic continued fractions:

Solve a differential equation with Sqrt:

Compute an elliptic integral from the Sqrt function:

Properties & Relations  (12)

Sqrt[x] and Surd[x,2] are the same for non-negative real values:

For negative reals, Sqrt gives an imaginary result, whereas the real-valued Surd reports an error:

Reduce combinations of square roots:

Evaluate power series involving square roots:

Expand a complex square root assuming variables are real valued:

Factor polynomials with square roots in coefficients:

Simplify handles expressions involving square roots:

There are many subtle issues in handling square roots for arbitrary complex arguments:

PowerExpand expands forms involving square roots:

It generically assumes that all variables are positive:

Finite sums of integers and square roots of integers are algebraic numbers:

Take limits accounting for branch cuts:

Sqrt can be represented as a DifferentialRoot:

The generating function for Sqrt:

Possible Issues  (3)

Square root is discontinuous across its branch cut along the negative real axis:

Sqrt[x^2] cannot automatically be reduced to x:

With x assumed positive, the simplification can be done:

Use PowerExpand to do the formal reduction:

Along the branch cut, these are not the same:

Neat Examples  (2)

Approximation to GoldenRatio:

Riemann surface for square root:

Wolfram Research (1988), Sqrt, Wolfram Language function, https://reference.wolfram.com/language/ref/Sqrt.html (updated 1996).

Text

Wolfram Research (1988), Sqrt, Wolfram Language function, https://reference.wolfram.com/language/ref/Sqrt.html (updated 1996).

CMS

Wolfram Language. 1988. "Sqrt." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Sqrt.html.

APA

Wolfram Language. (1988). Sqrt. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sqrt.html

BibTeX

@misc{reference.wolfram_2025_sqrt, author="Wolfram Research", title="{Sqrt}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Sqrt.html}", note=[Accessed: 17-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_sqrt, organization={Wolfram Research}, title={Sqrt}, year={1996}, url={https://reference.wolfram.com/language/ref/Sqrt.html}, note=[Accessed: 17-April-2025 ]}