TransferFunctionModel[g[s],s]
represents the model of the transfer-function matrix g[s] with complex variable s.
TransferFunctionModel[{n[s],d[s]},s]
specifies the numerator n[s] and denominator d[s] of a transfer-function model.
TransferFunctionModel[{z,p,g},s]
specifies the zeros z, poles p, and gain g of a transfer-function model.
gives the transfer-function model of the systems model sys.


TransferFunctionModel
TransferFunctionModel[g[s],s]
represents the model of the transfer-function matrix g[s] with complex variable s.
TransferFunctionModel[{n[s],d[s]},s]
specifies the numerator n[s] and denominator d[s] of a transfer-function model.
TransferFunctionModel[{z,p,g},s]
specifies the zeros z, poles p, and gain g of a transfer-function model.
gives the transfer-function model of the systems model sys.
Details and Options


- TransferFunctionModel is typically used for signal filters and control design.
- A continuous-time system modeled by
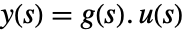 where
where 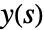 is the Laplace transform of the output,
is the Laplace transform of the output, 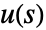 is the Laplace transform of the input and
is the Laplace transform of the input and 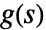 is the transfer matrix can be specified as TransferFunctionModel[g[s],s].
is the transfer matrix can be specified as TransferFunctionModel[g[s],s]. - A discrete-time system modeled by
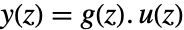 where
where 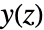 is the Z transform of the output,
is the Z transform of the output, 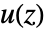 is the Z transform of the input and
is the Z transform of the input and 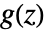 is the transfer matrix can be specified as TransferFunctionModel[g[z],z,SamplingPeriodτ].
is the transfer matrix can be specified as TransferFunctionModel[g[z],z,SamplingPeriodτ]. - Time delays can be included in any transfer-function model, by using SystemsModelDelay.
- In TransferFunctionModel[sys], the following systems can be converted:
-
AffineStateSpaceModel approximate Taylor conversion NonlinearStateSpaceModel approximate Taylor conversion StateSpaceModel exact conversion - TransferFunctionModel[…]["prop"] gives the value of the property "prop".
- TransferFunctionModel[…]["Properties"] gives the list of available properties.
- The following options can be given:
-
Appearance Automatic model appearance Method Automatic the method to obtain the transfer function of a state-space model SamplingPeriod Automatic the sampling period of the system SystemsModelLabels Automatic labels for the input and output variables ExternalTypeSignature Automatic variable types for embedded code - The option Appearance can take values Automatic, "Detailed", "Structured", "Elided", and "Iconized".
- Settings for the Method option include "DeterminantExpansion", "ResolventIdentities", "Inverse", and "Generic". With a setting Method->Automatic, the transfer-function model is computed using determinant expansion.
Examples
open all close allBasic Examples (5)
Scope (19)
A first-order continuous-time system:
A system with three zeros and six poles:
A first-order discrete-time system:
A two-input, one-output system:
A one-input, two-output system:
A two-input, two-output system:
Specify a transfer function using its numerator and denominator:
A MIMO transfer function specified in terms of its numerators and denominators:
A denominator polynomial that is the least common multiple:
Specify the transfer function, using its algebraic poles, zeros, and gains:
The transfer-function representation of a state-space model:
Taylor linearize an AffineStateSpaceModel and obtain its transfer function representation:
The linearization of an AffineStateSpaceModel with nonzero equilibrium values:
Taylor linearize a NonlinearStateSpaceModel:
Generalizations & Extensions (2)
Options (5)
SamplingPeriod (3)
Applications (18)
A proportional-integral (PI) controller:
A proportional-derivative (PD) controller:
A function to construct a proportional-integral-derivative (PID) controller:
A PID with specific gain values:
A function to construct a discrete-time PID controller:
A function for a continuous-time lead compensator:
A lead compensator for specific values of gain and pole-zero locations:
A function for a continuous-time lag compensator:
A digital lag compensator defined in terms of its zero and pole locations:
A general formula for analog lowpass Butterworth filters:
The general second-order transfer function:
Variations in damping ratio lead to qualitatively different responses:
A linearized inverted pendulum model:
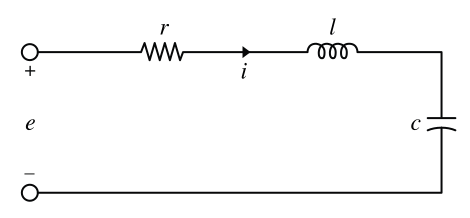
Transfer function between the input voltage and the shaft angular position of a DC motor:
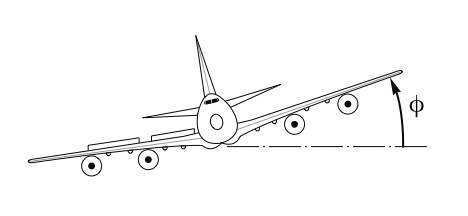
The aileron-to-roll-rate transfer function of an aircraft:
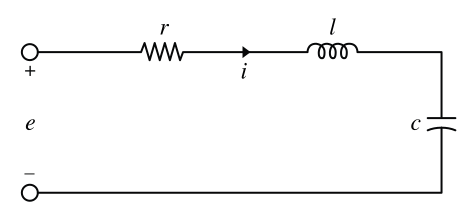
A temperature-controlled chemical reactor:
A MIMO transfer function describing an aircraft's longitudinal dynamics:
A ball mill grinding system with delay due to material transport:
Properties & Relations (6)
TransferFunctionModel behaves as a pure function of one argument:
The value of the transfer-function matrix at a specific frequency:
The values at several frequencies:
Use TransferFunctionFactor to obtain the factored form:
Use TransferFunctionCancel to cancel any common poles and zeros:
Find the element zeros and poles of a transfer-function matrix:
Possible Issues (3)
In TransferFunctionModel[m,var], pole-zero pairs may cancel before being processed:
Use Unevaluated to prevent cancellations:
Or use TransferFunctionModel[{num,den},var]:
Or TransferFunctionModel[{z,p,g},var]:
TransferFunctionModel[m,var] might result in a system with higher order:
Or simplify m before passing it to TransferFunctionModel:
If the complex variable var is not specified, it is assumed to be s for continuous-time systems:
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0)
Text
Wolfram Research (2010), TransferFunctionModel, Wolfram Language function, https://reference.wolfram.com/language/ref/TransferFunctionModel.html (updated 2014).
CMS
Wolfram Language. 2010. "TransferFunctionModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/TransferFunctionModel.html.
APA
Wolfram Language. (2010). TransferFunctionModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransferFunctionModel.html
BibTeX
@misc{reference.wolfram_2025_transferfunctionmodel, author="Wolfram Research", title="{TransferFunctionModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TransferFunctionModel.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_transferfunctionmodel, organization={Wolfram Research}, title={TransferFunctionModel}, year={2014}, url={https://reference.wolfram.com/language/ref/TransferFunctionModel.html}, note=[Accessed: 19-February-2026]}