Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

WaveletPhi

WaveletPhi[wave,x]

gives the scaling function for the symbolic wavelet wave evaluated at x.

WaveletPhi[wave]

gives the scaling function as a pure function.

Details and Options

The scaling function 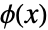satisfies the recursion equation 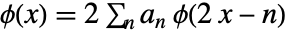, where 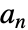are the lowpass filter coefficients.
WaveletPhi[wave,x,"Dual"] gives the dual scaling function 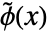for biorthogonal wavelets such as BiorthogonalSplineWavelet and ReverseBiorthogonalSplineWavelet.
The dual scaling function satisfies the recursion equation 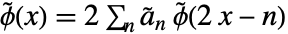, where 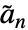are the dual lowpass filter coefficients.
The following options can be used:
MaxRecursion 8 number of recursive iterations to use

WorkingPrecision MachinePrecision precision to use in internal computations

Examples

open allclose all

Basic Examples (2)

Haar scaling function:

Symlet scaling function:

Scope (4)

Compute primal scaling function:

Dual scaling function:

Scaling function for HaarWavelet:

DaubechiesWavelet:

CoifletWavelet:

BiorthogonalSplineWavelet:

ReverseBiorthogonalSplineWavelet:

ShannonWavelet:

BattleLemarieWavelet:

Multivariate scaling and wavelet functions are products of univariate ones:

Options (3)

MaxRecursion (1)

Plot scaling function using different levels of recursion:

WorkingPrecision (2)

By default WorkingPrecision->MachinePrecision is used:

Use higher-precision filter computation:

Properties & Relations (4)

Scaling function integrates to unity :

In particular, :

satisfies the recursion equation :

Plot the components and the sum of the recursion:

Frequency response for is given by :

The filter is a lowpass filter:

Fourier transform of is given by :

Neat Examples (1)

Plot translates and dilations of scaling function:

Top