Basic Objects
Basic Objects
Expressions can be written in the form h[e1,e2,…]. The object h is known generically as the head of the expression. The ei are termed the elements of the expression. Both the head and the elements may themselves be expressions.
The parts of an expression can be referred to by numerical indices. The head has index 0; element ei has index i. Part[expr,i] or expr[[i]] gives the part of expr with index i. Negative indices count from the end.
Part[expr,i1,i2,…], expr[[i1,i2,…]], or Extract[expr,{i1,i2,…}] gives the piece of expr found by successively extracting parts of subexpressions with indices i1,i2,…. If you think of expressions as trees, the indices specify which branch to take at each node as you descend from the root.
The pieces of an expression that are specified by giving a sequence of exactly n indices are defined to be at level n in the expression. You can use levels to determine the domain of application of functions like Map. Level 0 corresponds to the whole expression.
The depth of an expression is defined to be the maximum number of indices needed to specify any part of the expression, plus one. A negative level number -n refers to all parts of an expression that have depth n.
The name of a symbol must be a sequence of letters, letter‐like forms, and digits, not starting with a digit. Uppercase and lowercase letters are always distinguished in the Wolfram Language.
| aaaaa | user‐defined symbol |
| Aaaaa | system‐defined symbol |
| $Aaaa | global or internal system‐defined symbol |
| aaaa$ | symbol renamed in a scoping construct |
| aa$nn | unique local symbol generated in a module |
Essentially all system‐defined symbols have names that contain only ordinary English letters, together with numbers and $. The exceptions are 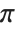 ,
, 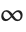 ,
, 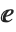 ,
,  and
and 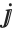 .
.
System‐defined symbols conventionally have names that consist of one or more complete English words. The first letter of each word is capitalized, and the words are run together.
Once created, an ordinary symbol in the Wolfram Language continues to exist unless it is explicitly removed using Remove. However, symbols created automatically in scoping constructs such as Module carry the attribute Temporary, which specifies that they should automatically be removed as soon as they no longer appear in any expression.
When a new symbol is to be created, the Wolfram Language first applies any value that has been assigned to $NewSymbol to strings giving the name of the symbol and the context in which the symbol would be created.
If the message General::newsym is switched on, then the Wolfram Language reports new symbols that are created. This message is switched off by default. Symbols created automatically in scoping constructs are not reported.
The full name of any symbol in the Wolfram Language consists of two parts: a context and a short name. The full name is written in the form context`name. The context context` can contain the same characters as the short name. It may also contain any number of context mark characters `, and must end with a context mark.
At any point in a Wolfram Language session, there is a current context $Context and a context search path $ContextPath consisting of a list of contexts. Symbols in the current context, or in contexts on the context search path, can be specified by giving only their short names, provided they are not shadowed by another symbol with the same short name.
| name | |
| `name | search $Context only; create there if necessary |
| context`name | search context only; create there if necessary |
| `context`name | search $Context`context only; create there if necessary |
With Wolfram Language packages, it is conventional to associate contexts whose names correspond to the names of the packages. Packages typically use BeginPackage and EndPackage to define objects in the appropriate context, and to add the context to the global $ContextPath. EndPackage prints a warning about any symbols that were created in a package but which are "shadowed" by existing symbols on the context search path.
The context is included in the printed form of a symbol only if it would be needed to specify the symbol at the time of printing.
All expressions in the Wolfram Language are ultimately made up from a small number of basic or atomic types of objects.
These objects have heads that are symbols that can be thought of as "tagging" their types. The objects contain "raw data", which can usually be accessed only by functions specific to the particular type of object. You can extract the head of the object using Head, but you cannot directly extract any of its other parts.
These basic objects in the Wolfram Language are considered to have depth 1 (as returned by Depth) and yield True when tested with AtomQ.
| Integer | integer nnnn |
| Real | approximate real number nnn.nnn |
| Rational | rational number nnn/nnn |
| Complex | complex number nnn+nnn I |
All numbers in the Wolfram Language can contain any number of digits. The Wolfram Language does exact computations when possible with integers and rational numbers, and with complex numbers whose real and imaginary parts are integers or rational numbers.
There are two types of approximate real numbers in the Wolfram Language: arbitrary precision and machine precision. In manipulating arbitrary‐precision numbers, the Wolfram Language tries to modify the precision so as to ensure that all digits actually given are correct.
With machine‐precision numbers, all computations are done to the same fixed precision, so some digits given may not be correct.
Unless otherwise specified, the Wolfram Language treats as machine‐precision numbers all approximate real numbers that lie between $MinMachineNumber and $MaxMachineNumber and that are input with less than $MachinePrecision digits.
In InputForm, the Wolfram Language prints machine‐precision numbers with $MachinePrecision digits, except when trailing digits are zero.
In any implementation of the Wolfram Language, the magnitudes of numbers (except 0) must lie between $MinNumber and $MaxNumber. Numbers with magnitudes outside this range are represented by Underflow[] and Overflow[].
Character strings in the Wolfram Language can contain any sequence of characters. They are input in the form "ccccc".
The individual characters can be printable ASCII (with character codes between 32 and 126), or in general any 8‐, 16‐ or 21-bit characters. The Wolfram Language uses the Unicode character set for 16‐ and 21-bit characters.
In FullForm, 16- and 21-bit characters are represented when possible in the form ∖[Name], and otherwise as ∖:nnnn and ∖|nnnnnn, respectively.