Evaluation of Expressions
Evaluation of Expressions
The fundamental operation that the Wolfram Language performs is evaluation. Whenever you enter an expression, the Wolfram Language evaluates the expression, then returns the result.
Evaluation in the Wolfram Language works by applying a sequence of definitions. The definitions can either be ones you explicitly entered, or ones that are built into the Wolfram Language.
Thus, for example, the Wolfram Language evaluates the expression 6+7 using a built‐in procedure for adding integers. Similarly, the Wolfram Language evaluates the algebraic expression x-3x+1 using a built‐in simplification procedure. If you had made the definition x=5, then the Wolfram Language would use this definition to reduce x-3x+1 to -9.
The two most central concepts in the Wolfram Language are probably expressions and evaluation. "Expressions" discusses how all the different kinds of objects that the Wolfram Language handles are represented in a uniform way using expressions. This tutorial describes how all the operations that the Wolfram Language can perform can also be viewed in a uniform way as examples of evaluation.
The Wolfram Language is an infinite evaluation system. When you enter an expression, the Wolfram Language will keep on using definitions it knows until it gets a result to which no definitions apply.
If you ask for fac[10], the Wolfram Language will keep on applying the definitions you have given until the result it gets no longer changes:
When the Wolfram Language has used all the definitions it knows, it gives whatever expression it has obtained as the result. Sometimes the result may be an object such as a number. But usually the result is an expression in which some objects are represented in a symbolic form.
The Wolfram Language uses its built‐in definitions for simplifying sums, but knows no definitions for f[3], so leaves this in symbolic form:
The Wolfram Language follows the principle of applying definitions until the result it gets no longer changes. This means that if you take the final result that the Wolfram Language gives, and enter it as Wolfram Language input, you will get back the same result again. (There are some subtle cases discussed in "Controlling Infinite Evaluation" in which this does not occur.)
At any given time, the Wolfram Language can only use those definitions that it knows at that time. If you add more definitions later, however, the Wolfram Language will be able to use these. The results you get from the Wolfram Language may change in this case.
The simplest examples of evaluation involve using definitions such as f[x_]=x^2 which transform one expression directly into another. But evaluation is also the process used to execute programs written in the Wolfram Language. Thus, for example, if you have a procedure consisting of a sequence of Wolfram Language expressions, some perhaps representing conditionals and loops, the execution of this procedure corresponds to the evaluation of these expressions. Sometimes the evaluation process may involve evaluating a particular expression several times, as in a loop.
The built‐in functions in the Wolfram Language operate in a wide variety of ways. But many of the mathematical functions share an important approach: they are set up so as to reduce classes of mathematical expressions to standard forms.
The built‐in definitions for the Plus function, for example, are set up to write any sum of terms in a standard unparenthesized form. The associativity of addition means that expressions like (a+b)+c, a+(b+c) and a+b+c are all equivalent. But for many purposes it is convenient for all these forms to be reduced to the single standard form a+b+c. The built‐in definitions for Plus are set up to do this.
Through the built‐in definitions for Plus, this expression is reduced to a standard unparenthesized form:
Whenever the Wolfram Language knows that a function is associative, it tries to remove parentheses (or nested invocations of the function) to get the function into a standard "flattened" form.
A function like addition is not only associative, but also commutative, which means that expressions like a+c+b and a+b+c with terms in different orders are equal. Once again, the Wolfram Language tries to put all such expressions into a "standard" form. The standard form it chooses is the one in which all the terms are in a definite order, corresponding roughly to alphabetical order.
Two important properties that the Wolfram Language uses in reducing certain functions to standard form.
There are several reasons to try to put expressions into standard forms. The most important is that if two expressions are really in standard form, it is obvious whether or not they are equal.
When the two sums are put into standard order, they are immediately seen to be equal, so that two f's cancel, leaving the result 0:
You could imagine finding out whether a+c+b was equal to c+a+b by testing all possible orderings of each sum. It is clear that simply reducing both sums to standard form is a much more efficient procedure.
One might think that the Wolfram Language should somehow automatically reduce all mathematical expressions to a single standard canonical form. With all but the simplest kinds of expressions, however, it is quite easy to see that you do not want the same standard form for all purposes.
For polynomials, for example, there are two obvious standard forms, which are good for different purposes. The first standard form for a polynomial is a simple sum of terms, as would be generated in the Wolfram Language by applying the function Expand. This standard form is most appropriate if you need to add and subtract polynomials.
There is, however, another possible standard form that you can use for polynomials. By applying Factor, you can write any polynomial as a product of irreducible factors. This canonical form is useful if you want to do operations like division.
Expanded and factored forms are in a sense both equally good standard forms for polynomials. Which one you decide to use simply depends on what you want to use it for. As a result, the Wolfram Language does not automatically put polynomials into one of these two forms. Instead, it gives you functions like Expand and Factor that allow you explicitly to put polynomials in whatever form you want.
You can write both of them in expanded form just by applying Expand. In this form, the equality of the polynomials is obvious:
Although it is clear that you do not always want expressions reduced to the same standard form, you may wonder whether it is at least possible to reduce all expressions to some standard form.
There is a basic result in the mathematical theory of computation which shows that this is, in fact, not always possible. You cannot guarantee that any finite sequence of transformations will take any two arbitrarily chosen expressions to a standard form.
In a sense, this is not particularly surprising. If you could in fact reduce all mathematical expressions to a standard form, then it would be quite easy to tell whether any two expressions were equal. The fact that so many of the difficult problems of mathematics can be stated as questions about the equality of expressions suggests that this can in fact be difficult.
Definitions such as f[x_]=x^2 specify values for functions. Sometimes, however, you need to specify general properties of functions, without necessarily giving explicit values.
The Wolfram Language provides a selection of attributes that you can use to specify various properties of functions. For example, you can use the attribute Flat to specify that a particular function is "flat", so that nested invocations are automatically flattened, and it behaves as if it were associative.
Now f behaves as a flat, or associative, function, so that nested invocations are automatically flattened:
Attributes like Flat can affect not only evaluation, but also operations such as pattern matching. If you give definitions or transformation rules for a function, you must be sure to have specified the attributes of the function first.
| Attributes[f] | give the attributes of f |
| Attributes[f]={attr1,attr2,…} | set the attributes of f |
| Attributes[f]={} | set f to have no attributes |
| SetAttributes[f,attr] | add attr to the attributes of f |
| ClearAttributes[f,attr] | remove attr from the attributes of f |
| Orderless |
orderless, commutative function (arguments are sorted into standard order)
|
| Flat |
flat, associative function (arguments are "flattened out")
|
| OneIdentity | f[f[a]], etc. are equivalent to a for pattern matching |
| Listable | f is automatically "threaded" over lists that appear as arguments (e.g., f[{a,b}] becomes {f[a],f[b]}) |
| Constant | all derivatives of f are zero |
| NumericFunction | f is assumed to have a numerical value when its arguments are numeric quantities |
| Protected | values of f cannot be changed |
| Locked | attributes of f cannot be changed |
| ReadProtected | values of f cannot be read |
| HoldFirst | the first argument of f is not evaluated |
| HoldRest | all but the first argument of f are not evaluated |
| HoldAll | none of the arguments of f are evaluated |
| HoldAllComplete | the arguments of f are treated as completely inert |
| NHoldFirst | the first argument of f is not affected by N |
| NHoldRest | all but the first argument of f are not affected by N |
| NHoldAll | none of the arguments of f are affected by N |
| SequenceHold | Sequence objects appearing in the arguments of f are not flattened out |
| Temporary |
f
is a local variable, removed when no longer used
|
| Stub | Needs is automatically called if f is ever explicitly input |
An important attribute assigned to built‐in mathematical functions in the Wolfram Language is the attribute Listable. This attribute specifies that a function should automatically be distributed or "threaded" over lists that appear as its arguments. This means that the function effectively gets applied separately to each element in any lists that appear as its arguments.
Many of the attributes you can assign to functions in the Wolfram Language directly affect the evaluation of those functions. Some attributes, however, affect only other aspects of the treatment of functions. For example, the attribute OneIdentity affects only pattern matching, as discussed in "Flat and Orderless Functions". Similarly, the attribute Constant is only relevant in differentiation, and operations that rely on differentiation.
The Protected attribute affects assignments. The Wolfram Language does not allow you to make any definition associated with a symbol that carries this attribute. The functions Protect and Unprotect discussed in "Modifying Built-in Functions" can be used as alternatives to SetAttributes and ClearAttributes to set and clear this attribute. As discussed in "Modifying Built-in Functions", most built‐in Wolfram Language objects are initially protected so that you do not make definitions for them by mistake.
You can usually see the definitions you have made for a particular symbol by typing ?f, or by using a variety of built‐in Wolfram Language functions. However, if you set the attribute ReadProtected, the Wolfram Language will not allow you to look at the definition of a particular symbol. It will nevertheless continue to use the definitions in performing evaluation.
Functions like SetAttributes and ClearAttributes usually allow you to modify the attributes of a symbol in any way. However, if you once set the Locked attribute on a symbol, then the Wolfram Language will not allow you to modify the attributes of that symbol for the remainder of your Wolfram System session. Using the Locked attribute in addition to Protected or ReadProtected, you can arrange for it to be impossible for users to modify or read definitions.
By defining attributes for a function you specify properties that the Wolfram Language should assume whenever that function appears. Often, however, you want to assume the properties only in a particular instance. In such cases, you will be better off not to use attributes, but instead to call a particular function to implement the transformation associated with the attributes.
By explicitly calling Thread, you can implement the transformation that would be done automatically if p were listable:
Attributes in the Wolfram Language can only be permanently defined for single symbols. However, the Wolfram Language also allows you to set up pure functions which behave as if they carry attributes.
| Function[vars,body,{attr1,…}] | a pure function with attributes attr1, … |
By adding the attribute Listable, the function gets distributed over the elements of the list before applying p:
Here the standard procedure used by the Wolfram System to evaluate expressions is described. This procedure is the one followed for most kinds of expression. There are, however, some kinds of expressions, such as those used to represent the Wolfram System programs and control structures, that are evaluated in a nonstandard way.
In the standard evaluation procedure, the Wolfram System first evaluates the head of an expression and then evaluates each element of the expression. These elements are in general themselves expressions, to which the same evaluation procedure is recursively applied.
The three Print functions are evaluated in turn, each printing its argument, then returning the value Null:
As soon as the Wolfram System has evaluated the head of an expression, it sees whether the head is a symbol that has attributes. If the symbol has the attributes Orderless, Flat, or Listable, then immediately after evaluating the elements of the expression the Wolfram System performs the transformations associated with these attributes.
The next step in the standard evaluation procedure is to use definitions that the Wolfram System knows for the expression it is evaluating. The Wolfram System first tries to use definitions that you have made, and if there are none that apply, it tries built‐in definitions.
If the Wolfram System finds a definition that applies, it performs the corresponding transformation on the expression. The result is another expression, which must then in turn be evaluated according to the standard evaluation procedure.
■ Evaluate the head of the expression. |
■ Evaluate each element in turn. |
■ Apply any definitions that you have given. |
■ Apply any built‐in definitions. |
■ Evaluate the result. |
As discussed in "Principles of Evaluation", the Wolfram System follows the principle that each expression is evaluated until no further definitions apply. This means that the Wolfram System must continue reevaluating results until it gets an expression that remains unchanged through the evaluation procedure.
Here is an example that shows how the standard evaluation procedure works on a simple expression. Assume that a=7.
| 2ax+a^2+1 | here is the original expression |
| Plus[Times[2,a,x],Power[a,2],1] | this is the internal form |
| Times[2,a,x] | this is evaluated first |
| Times[2,7,x] | a is evaluated to give 7 |
| Times[14,x] | built‐in definitions for Times give this result |
| Power[a,2] | this is evaluated next |
| Power[7,2] | here is the result after evaluating a |
| 49 | built‐in definitions for Power give this result |
| Plus[Times[14,x],49,1] | here is the result after the arguments of Plus have been evaluated |
| Plus[50,Times[14,x]] | built‐in definitions for Plus give this result |
| 50+14x | the result is printed like this |
The Wolfram System provides various ways to "trace" the evaluation process, as discussed in "Tracing Evaluation". The function Trace[expr] gives a nested list showing each subexpression generated during evaluation. (Note that the standard evaluation traverses the expression tree in a depth‐first way, so that the smallest subparts of the expression appear first in the results of Trace.)
This gives a nested list of all the subexpressions generated during the evaluation of the expression:
The order in which the Wolfram System applies different kinds of definitions is important. The fact that the Wolfram System applies definitions you have given before it applies built‐in definitions means that you can give definitions that override the built‐in ones, as discussed in "Modifying Built-in Functions".
You can give your own definitions for ArcSin. You need to remove the protection attribute first:
As discussed in "Associating Definitions with Different Symbols", you can associate definitions with symbols either as upvalues or downvalues. The Wolfram System always tries upvalue definitions before downvalue ones.
If you have an expression like f[g[x]], there are, in general, two sets of definitions that could apply: downvalues associated with f and upvalues associated with g. The Wolfram System tries the definitions associated with g before those associated with f.
This ordering follows the general strategy of trying specific definitions before more general ones. By applying upvalues associated with arguments before applying downvalues associated with a function, the Wolfram System allows you to make definitions for special arguments that override the general definitions for the function with any arguments.
■ Definitions associated with g are applied before definitions associated with f in the expression f[g[x]]. |
Most functions such as Plus that are built into the Wolfram System have downvalues. There are, however, some objects in the Wolfram System that have built‐in upvalues. For example, SeriesData objects, which represent power series, have built‐in upvalues with respect to various mathematical operations.
For an expression like f[g[x]], the complete sequence of definitions that are tried in the standard evaluation procedure is:
- Definitions you have given associated with g;
- Built‐in definitions associated with g;
- Definitions you have given associated with f;
- Built‐in definitions associated with f.
The fact that upvalues are used before downvalues is important in many situations. In a typical case, you might want to define an operation such as composition. If you give upvalues for various objects with respect to composition, these upvalues will be used whenever such objects appear. However, you can also give a general procedure for composition, to be used if no special objects are present. You can give this procedure as a downvalue for composition. Since downvalues are tried after upvalues, the general procedure will be used only if no objects with upvalues are present.
In general, there can be several objects that have upvalues in a particular expression. The Wolfram System first looks at the head of the expression and tries any upvalues associated with it. Then it successively looks at each element of the expression, trying any upvalues that exist. The Wolfram System performs this procedure first for upvalues that you have explicitly defined, and then for upvalues that are built-in. The procedure means that in a sequence of elements, upvalues associated with earlier elements take precedence over those associated with later elements.
While most built‐in Wolfram Language functions follow the standard evaluation procedure, some important ones do not. For example, most of the Wolfram Language functions associated with the construction and execution of programs use non‐standard evaluation procedures. In typical cases, the functions either never evaluate some of their arguments, or do so in a special way under their own control.
| x=y | do not evaluate the left‐hand side |
| If[p,a,b] | |
| Do[expr,{n}] | evaluate expr n times |
| Plot[f,{x,…}] | evaluate f with a sequence of numerical values for x |
| Function[{x},body] | do not evaluate until the function is applied |
When you give a definition such as a=1, the Wolfram Language does not evaluate the a that appears on the left‐hand side. You can see that there would be trouble if the a was evaluated. The reason is that if you had previously set a=7, then evaluating a in the definition a=1 would put the definition into the nonsensical form 7=1.
In the standard evaluation procedure, each argument of a function is evaluated in turn. This is prevented by setting the attributes HoldFirst, HoldRest and HoldAll. These attributes make the Wolfram Language "hold" particular arguments in an unevaluated form.
| HoldFirst | do not evaluate the first argument |
| HoldRest | evaluate only the first argument |
| HoldAll | evaluate none of the arguments |
Even though a function may have attributes which specify that it should hold certain arguments unevaluated, you can always explicitly tell the Wolfram Language to evaluate those arguments by giving the arguments in the form Evaluate[arg].
Evaluate effectively overrides the HoldFirst attribute, and causes the first argument to be evaluated:
| f[Evaluate[arg]] | evaluate arg immediately, even though attributes of f may specify that it should be held |
By holding its arguments, a function can control when those arguments are evaluated. By using Evaluate, you can force the arguments to be evaluated immediately, rather than being evaluated under the control of the function. This capability is useful in a number of circumstances.
The Wolfram Language Set function holds its first argument, so the symbol a is not evaluated in this case:
You can make Set evaluate its first argument using Evaluate. In this case, the result is the object which is the value of a, namely b is set to 6:
In most cases, you want all expressions you give to the Wolfram Language to be evaluated. Sometimes, however, you may want to prevent the evaluation of certain expressions. For example, if you want to manipulate pieces of a Wolfram Language program symbolically, then you must prevent those pieces from being evaluated while you are manipulating them.
You can use the functions Hold and HoldForm to keep expressions unevaluated. These functions work simply by carrying the attribute HoldAll, which prevents their arguments from being evaluated. The functions provide "wrappers" inside which expressions remain unevaluated.
The difference between Hold[expr] and HoldForm[expr] is that in standard Wolfram Language output format, Hold is printed explicitly, while HoldForm is not. If you look at the full internal Wolfram Language form, you can however see both functions.
Hold maintains expressions in an unevaluated form:
HoldForm also keeps expressions unevaluated, but is invisible in standard Wolfram Language output format:
HoldForm is still present internally:
| Hold[expr] | keep expr unevaluated |
| HoldComplete[expr] | keep expr unevaluated and prevent upvalues associated with expr from being used |
| HoldForm[expr] | |
| ReleaseHold[expr] | |
| Extract[expr,index,Hold] |
This extracts a part and immediately wraps it with Hold, so it does not get evaluated:
| f[…,Unevaluated[expr],…] | give expr unevaluated as an argument to f |
Unevaluated[expr] effectively works by temporarily giving a function an attribute like HoldFirst, and then supplying expr as an argument to the function.
| SequenceHold | do not flatten out Sequence objects that appear as arguments |
| HoldAllComplete | treat all arguments as completely inert |
By setting the attribute HoldAll, you can prevent the Wolfram Language from evaluating the arguments of a function. But even with this attribute set, the Wolfram Language will still do some transformations on the arguments. By setting SequenceHold you can prevent it from flattening out Sequence objects that appear in the arguments. And by setting HoldAllComplete you can also inhibit the stripping of Unevaluated, and prevent the Wolfram Language from using any upvalues it finds associated with the arguments.
There are a number of important interactions in the Wolfram Language between evaluation and pattern matching. The first observation is that pattern matching is usually done on expressions that have already been at least partly evaluated. As a result, it is usually appropriate that the patterns to which these expressions are matched should themselves be evaluated.
There are some cases, however, where you may want to keep all or part of a pattern unevaluated. You can do this by wrapping the parts you do not want to evaluate with HoldPattern. In general, whenever HoldPattern[patt] appears within a pattern, this form is taken to be equivalent to patt for the purpose of pattern matching, but the expression patt is maintained unevaluated.
| HoldPattern[patt] | equivalent to patt for pattern matching, with patt kept unevaluated |
One application for HoldPattern is in specifying patterns which can apply to unevaluated expressions, or expressions held in an unevaluated form.
HoldPattern keeps the 1+1 from being evaluated, and allows it to match the 1+1 on the left‐hand side of the /. operator:
Notice that while functions like Hold prevent evaluation of expressions, they do not affect the manipulation of parts of those expressions with /. and other operators.
As illustrated above, the left‐hand sides of transformation rules such as lhs->rhs are usually evaluated immediately, since the rules are usually applied to expressions which have already been evaluated. The right‐hand side of lhs->rhs is also evaluated immediately. With the delayed rule lhs:>rhs, however, the expression rhs is not evaluated.
Here are the results of applying the rules. The right‐hand side of the :> rule gets inserted inside the Hold without evaluation:
While the left‐hand sides of transformation rules are usually evaluated, the left‐hand sides of definitions are usually not. The reason for the difference is as follows. Transformation rules are typically applied using /. to expressions that have already been evaluated. Definitions, however, are used during the evaluation of expressions, and are applied to expressions that have not yet been completely evaluated. To work on such expressions, the left‐hand sides of definitions must be maintained in a form that is at least partially unevaluated.
Definitions for symbols are the simplest case. As discussed in "Non‐Standard Evaluation", a symbol on the left‐hand side of a definition such as x=value is not evaluated. If x had previously been assigned a value y, then if the left‐hand side of x=value were evaluated, it would turn into the quite unrelated definition y=value.
If you evaluate the left‐hand side, then you define not the symbol k, but the value w[4] of the symbol k:
Although individual symbols that appear on the left‐hand sides of definitions are not evaluated, more complicated expressions are partially evaluated. In an expression such as f[args] on the left‐hand side of a definition, the args are evaluated.
You can see why the arguments of a function that appears on the left‐hand side of a definition must be evaluated by considering how the definition is used during the evaluation of an expression. As discussed in "Principles of Evaluation", when the Wolfram Language evaluates a function, it first evaluates each of the arguments, then tries to find definitions for the function. As a result, by the time the Wolfram Language applies any definition you have given for a function, the arguments of the function must already have been evaluated. An exception to this occurs when the function in question has attributes which specify that it should hold some of its arguments unevaluated.
| symbol=value | symbol is not evaluated; value is evaluated |
| symbol:=value | neither symbol nor value is evaluated |
| f[args]=value | args are evaluated; left‐hand side as a whole is not |
| f[HoldPattern[arg]]=value |
f
[
arg
]
is assigned, without evaluating
arg
|
| Evaluate[lhs]=value | left‐hand side is evaluated completely |
While in most cases it is appropriate for the arguments of a function that appears on the left‐hand side of a definition to be evaluated, there are some situations in which you do not want this to happen. In such cases, you can wrap HoldPattern around the parts that you do not want to be evaluated.
The built‐in Wolfram Language iteration functions such as Table and Sum evaluate their arguments in a slightly special way.
When evaluating an expression like Table[f,{i,imax}], the first step, as discussed in "Blocks and Local Values", is to make the value of i local. Next, the limit imax in the iterator specification is evaluated. The expression f is maintained in an unevaluated form, but is repeatedly evaluated as a succession of values are assigned to i. When this is finished, the global value of i is restored.
The function RandomReal[] is evaluated four separate times here, so four different pseudorandom numbers are generated:
This evaluates RandomReal[] before feeding it to Table. The result is a list of four identical numbers:
In most cases, it is convenient for the function f in an expression like Table[f,{i,imax}] to be maintained in an unevaluated form until specific values have been assigned to i. This is true in particular if a complete symbolic form for f valid for any i cannot be found.
This defines fac to give the factorial when it has an integer argument, and to give NaN (standing for "Not a Number") otherwise:
In cases where a complete symbolic form for f with arbitrary i in expressions such as Table[f,{i,imax}] can be found, it is often more efficient to compute this form first, and then feed it to Table. You can do this using Table[Evaluate[f],{i,imax}].
By inserting Evaluate, you tell the Wolfram Language first to evaluate the sum symbolically, then to iterate over i:
| Table[f,{i,imax}] | keep f unevaluated until specific values are assigned to i |
| Table[Evaluate[f],{i,imax}] | evaluate f first with i left symbolic |
The Wolfram Language provides various ways to set up conditionals, which specify that particular expressions should be evaluated only if certain conditions hold.
| lhs:=rhs/;test | use the definition only if test evaluates to True |
| If[test,then,else] | |
| Which[test1,value1,test2,…] | |
| Switch[expr,form1,value1,form2,…] | compare expr with each of the formi, giving the value associated with the first form it matches |
| Switch[expr,form1,value1,form2,…,_,def] | use def as a default value |
| Piecewise[{{value1,test1},…},def] | give the value corresponding to the first testi which yields True |
When you write programs in the Wolfram Language, you will often have a choice between making a single definition whose right‐hand side involves several branches controlled by If functions, or making several definitions, each controlled by an appropriate /; condition. By using several definitions, you can often produce programs that are both clearer, and easier to modify.
The function If provides a way to choose between two alternatives. Often, however, there will be more than two alternatives. One way to handle this is to use a nested set of If functions. Usually, however, it is instead better to use functions like Which and Switch.
This defines a function with three regions. Using True as the third test makes this the default case:
This uses the first case in the Which:
An important point about symbolic systems such as the Wolfram Language is that the conditions you give may yield neither True nor False. Thus, for example, the condition x==y does not yield True or False unless x and y have specific values, such as numerical ones.
You can add a special fourth argument to If, which is used if the test does not yield True or False:
| If[test,then,else,unknown] | |
| TrueQ[expr] | |
| lhs===rhs or SameQ[lhs,rhs] | |
| lhs=!=rhs or UnsameQ[lhs,rhs] | |
| MatchQ[expr,form] |
The main difference between lhs===rhs and lhs==rhs is that === always returns True or False, whereas == can leave its input in symbolic form, representing a symbolic equation, as discussed in "Equations". You should typically use === when you want to test the structure of an expression, and == if you want to test mathematical equality. The Wolfram Language pattern matcher effectively uses === to determine when one literal expression matches another.
In setting up conditionals, you will often need to use combinations of tests, such as test1&&test2&&…. An important point is that the result from this combination of tests will be False if any of the testi yield False. The Wolfram Language always evaluates the testi in turn, stopping if any of the testi yield False.
| expr1&&expr2&&expr3 | evaluate until one of the expri is found to be False |
| expr1||expr2||expr3 | evaluate until one of the expri is found to be True |
Here the first test yields False, so the second test is not tried. The second test would involve 1/0, and would generate an error:
The way that the Wolfram Language evaluates logical expressions allows you to combine sequences of tests where later tests may make sense only if the earlier ones are satisfied. The behavior, which is analogous to that found in languages such as C, is convenient in constructing many kinds of Wolfram Language programs.
The execution of a Wolfram Language program involves the evaluation of a sequence of Wolfram Language expressions. In simple programs, the expressions to be evaluated may be separated by semicolons, and evaluated one after another. Often, however, you need to evaluate expressions several times, in some kind of "loop".
| Do[expr,{i,imax}] | evaluate expr repetitively, with i varying from 1 to imax in steps of 1 |
| Do[expr,{i,imin,imax,di}] | evaluate expr with i varying from imin to imax in steps of di |
| Do[expr,{i,list}] | evaluate expr with i taking on values from list |
| Do[expr,{n}] | evaluate expr n times |
The way iteration is specified in Do is exactly the same as in functions like Table and Sum. Just as in those functions, you can set up several nested loops by giving a sequence of iteration specifications to Do.
Sometimes you may want to repeat a particular operation a certain number of times, without changing the value of an iteration variable. You can specify this kind of repetition in Do just as you can in Table and other iteration functions.
You can put a procedure inside Do:
| Nest[f,expr,n] | apply f to expr n times |
| FixedPoint[f,expr] | start with expr, and apply f repeatedly until the result no longer changes |
| NestWhile[f,expr,test] |
Do allows you to repeat operations by evaluating a particular expression many times with different values for iteration variables. Often, however, you can make more elegant and efficient programs using the functional programming constructs discussed in "Applying Functions Repeatedly". Nest[f,x,n], for example, allows you to apply a function repeatedly to an expression.
By nesting a pure function, you can get the same result as in the example with Do above:
Nest allows you to apply a function a specified number of times. Sometimes, however, you may simply want to go on applying a function until the results you get no longer change. You can do this using FixedPoint[f,x].
FixedPoint goes on applying a function until the result no longer changes:
You can use FixedPoint to imitate the evaluation process in the Wolfram Language, or the operation of functions such as expr//.rules. FixedPoint goes on until two successive results it gets are the same. NestWhile allows you to go on until an arbitrary function no longer yields True.
When the Throw is encountered, evaluation stops, and the current value of i is returned as the value of the enclosing Catch:
Throw and Catch provide a flexible way to control the process of evaluation in the Wolfram Language. The basic idea is that whenever a Throw is encountered, the evaluation that is then being done is stopped, and the Wolfram Language immediately returns to the nearest appropriate enclosing Catch.
Scan applies the function Print to each successive element in the list, and in the end just returns Null:
The evaluation of Scan stops as soon as Throw is encountered, and the enclosing Catch returns as its value the argument of Throw:
The same result is obtained with Map, even though Map would have returned a list if its evaluation had not been stopped by encountering a Throw:
You can use Throw and Catch to divert the operation of functional programming constructs, allowing for example the evaluation of such constructs to continue only until some condition has been met. Note that if you stop evaluation using Throw, then the structure of the result you get may be quite different from what you would have got if you had allowed the evaluation to complete.
Since there is no Throw encountered, the result here is just as before:
Now the evaluation of the NestList is diverted, and the single number given as the argument of Throw is returned:
Throw and Catch operate in a completely global way: it does not matter how or where a Throw is generated—it will always stop evaluation and return to the enclosing Catch.
The Throw stops the evaluation of f, and causes the Catch to return just a, with no trace of f left:
This defines a function which generates a Throw when its argument is larger than 10:
No Throw is generated here:
In small programs, it is often adequate to use Throw[value] and Catch[expr] in their simplest forms. But particularly if you write larger programs that contain many separate pieces, it is usually much better to use Throw[value,tag] and Catch[expr,form]. By keeping the expressions tag and form local to a particular piece of your program, you can then ensure that your Throw and Catch will also operate only within that piece.
But here it is caught only by the outer Catch:
You can use patterns in specifying the tags which a particular Catch should catch:
You should realize that there is no need for the tag that appears in Throw to be a constant; in general it can be any expression.
Here the inner Catch catches all throws with tags less than 4, and continues the Do. But as soon as the tag reaches 4, the outer Catch is needed:
When you use Catch[expr,form] with Throw[value,tag], the value returned by Catch is simply the expression value given in the Throw. If you use Catch[expr,form,f], however, then the value returned by Catch is instead f[value,tag].
| While[test,body] | |
| For[start,test,incr,body] | evaluate start, then repetitively evaluate body and incr, until test fails |
Functions like Do, Nest, and FixedPoint provide structured ways to make loops in Wolfram Language programs, while Throw and Catch provide opportunities for modifying this structure. Sometimes, however, you may want to create loops that even from the outset have less structure. And in such cases, you may find it convenient to use the functions While and For, which perform operations repeatedly, stopping when a specified condition fails to be true.
The While loop continues until the condition fails:
The functions While and For in the Wolfram Language are similar to the control structures while and for in languages such as C. Notice, however, that there are a number of important differences. For example, the roles of comma and semicolon are reversed in Wolfram Language For loops relative to C language ones.
Here is a more complicated For loop. Notice that the loop terminates as soon as the test i^2<10 fails:
In the Wolfram Language, both While and For always evaluate the loop test before evaluating the body of the loop. As soon as the loop test fails to be True, While and For terminate. The body of the loop is thus only evaluated in situations where the loop test is True.
In a While or For loop, or in general in any Wolfram Language procedure, the Wolfram Language expressions you give are evaluated in a definite sequence. You can think of this sequence as defining the "flow of control" in the execution of a Wolfram Language program.
In most cases, you should try to keep the flow of control in your Wolfram Language programs as simple as possible. The more the flow of control depends for example on specific values generated during the execution of the program, the more difficult you will typically find it to understand the structure and operation of the program.
Functional programming constructs typically involve very simple flow of control. While and For loops are always more complicated, since they are set up to make the flow of control depend on the values of the expressions given as tests. Nevertheless, even in such loops, the flow of control does not usually depend on the values of expressions given in the body of the loop.
In some cases, however, you may need to construct Wolfram Language programs in which the flow of control is affected by values generated during the execution of a procedure or of the body of a loop. One way to do this, which fits in with functional programming ideas, is to use Throw and Catch. But the Wolfram Language also provides various functions for modifying the flow of control which work like in languages such as C.
| Break[] | exit the nearest enclosing loop |
| Continue[] | go to the next step in the current loop |
| Return[expr] | return the value expr from a function |
| Goto[name] | go to the element Label[name] in the current procedure |
| Throw[value] |
Return[expr] allows you to exit a particular function, returning a value. You can think of Throw as a kind of nonlocal return which allows you to exit a whole sequence of nested functions. Such behavior can be convenient for handling certain error conditions.
Here is an example of the use of Return. This particular procedure could equally well have been written without using Return:
When the argument is greater than 5, the first Return in the procedure is used:
No Throw is generated here:
Functions like Continue[] and Break[] allow you to "transfer control" to the beginning or end of a loop in a Wolfram Language program. Sometimes you may instead need to transfer control to a particular element in a Wolfram Language procedure. If you give a Label as an element in a procedure, you can use Goto to transfer control to this element.
Note that you can use Goto in a particular Wolfram Language procedure only when the Label it specifies occurs as an element of the same Wolfram Language procedure. In general, use of Goto reduces the degree of structure that can readily be perceived in a program, and therefore makes the operation of the program more difficult to understand.
In many computations you are concerned only with the final result of evaluating the expression given as input. But sometimes you also want to collect expressions that were generated in the course of the evaluation. You can do this using Sow and Reap.
This defines a function that can do a Sow:
| Sow[val,tag] | sow val with a tag to indicate when to reap |
| Sow[val,{tag1,tag2,…}] | sow val for each of the tagi |
| Reap[expr,form] | reap all values whose tags match form |
| Reap[expr,{form1,form2,…}] | make separate lists for each of the formi |
| Reap[expr,{form1,…},f] | apply f to each distinct tag and list of values |
The standard way in which the Wolfram System works is to take any expression you give as input, evaluate the expression completely, and then return the result. When you are trying to understand what the Wolfram System is doing, however, it is often worthwhile to look not just at the final result of evaluation, but also at intermediate steps in the evaluation process.
| Trace[expr] | generate a list of all expressions used in the evaluation of expr |
| Trace[expr,form] | include only expressions that match the pattern form |
Trace[expr] gives a list that includes all the intermediate expressions involved in the evaluation of expr. Except in rather simple cases, however, the number of intermediate expressions generated in this way is typically very large, and the list returned by Trace is difficult to understand.
Trace[expr,form] allows you to "filter" the expressions that Trace records, keeping only those that match the pattern form.
This gives all the intermediate expressions generated in the evaluation of fac[3]. The result is quite complicated:
You can specify any pattern in Trace:
Trace[expr,form] effectively works by intercepting every expression that is about to be evaluated during the evaluation of expr, and picking out those that match the pattern form.
If you want to trace "calls" to a function like fac, you can do so simply by telling Trace to pick out expressions of the form fac[n_]. You can also use patterns like f[n_,2] to pick out calls with particular argument structure.
A typical Wolfram System program, however, consists not only of "function calls" like fac[n], but also of other elements, such as assignments to variables, control structures, and so on. All of these elements are represented as expressions. As a result, you can use patterns in Trace to pick out any kind of Wolfram System program element. Thus, for example, you can use a pattern like k=_ to pick out all assignments to the symbol k.
Trace[expr,form] can pick out expressions that occur at any time in the evaluation of expr. The expressions need not, for example, appear directly in the form of expr that you give. They may instead occur, say, during the evaluation of functions that are called as part of the evaluation of expr.
Trace allows you to monitor intermediate steps in the evaluation not only of functions that you define, but also of some functions that are built into the Wolfram System. You should realize, however, that the specific sequence of intermediate steps followed by built‐in Wolfram System functions depends in detail on their implementation and optimization in a particular version of the Wolfram System.
| Trace[expr,f[___]] | show all calls to the function f |
| Trace[expr,i=_] | show assignments to i |
| Trace[expr,_=_] | show all assignments |
| Trace[expr,Message[___]] | show messages generated |
Some ways to use Trace.
The function Trace returns a list that represents the "history" of a Wolfram System computation. The expressions in the list are given in the order that they were generated during the computation. In most cases, the list returned by Trace has a nested structure, which represents the "structure" of the computation.
The basic idea is that each sublist in the list returned by Trace represents the "evaluation chain" for a particular Wolfram System expression. The elements of this chain correspond to different forms of the same expression. Usually, however, the evaluation of one expression requires the evaluation of a number of other expressions, often subexpressions. Each subsidiary evaluation is represented by a sublist in the structure returned by Trace.
The successive forms generated in the simplification of y+x+y show up as successive elements in its evaluation chain:
There are two basic ways that subsidiary evaluations can be required during the evaluation of a Wolfram System expression. The first way is that the expression may contain subexpressions, each of which has to be evaluated. The second way is that there may be rules for the evaluation of the expression that involve other expressions that themselves must be evaluated. Both kinds of subsidiary evaluations are represented by sublists in the structure returned by Trace.
You often get nested lists when you trace the evaluation of functions that are defined "recursively" in terms of other instances of themselves. The reason is typically that each new instance of the function appears as a subexpression in the expressions obtained by evaluating previous instances of the function.
Thus, for example, with the definition fac[n_]:=n fac[n-1], the evaluation of fac[6] yields the expression 6 fac[5], which contains fac[5] as a subexpression.
Each step in the evaluation of any Wolfram System expression can be thought of as the result of applying a particular transformation rule. As discussed in "Associating Definitions with Different Symbols", all the rules that the Wolfram System knows are associated with specific symbols or "tags". You can use Trace[expr,f] to see all the steps in the evaluation of expr that are performed using transformation rules associated with the symbol f. In this case, Trace gives not only the expressions to which each rule is applied, but also the results of applying the rules.
In general, Trace[expr,form] picks out all the steps in the evaluation of expr where form matches either the expression about to be evaluated, or the tag associated with the rule used.
| Trace[expr,f] | show all evaluations that use transformation rules associated with the symbol f |
| Trace[expr,f|g] | show all evaluations associated with either f or g |
| Trace[expr,form,TraceOn->oform] | switch on tracing only within forms matching oform |
| Trace[expr,form,TraceOff->oform] | switch off tracing within any form matching oform |
Trace[expr,form] allows you to trace expressions matching form generated at any point in the evaluation of expr. Sometimes, you may want to trace only expressions generated during certain parts of the evaluation of expr.
By setting the option TraceOn->oform, you can specify that tracing should be done only during the evaluation of forms that match oform. Similarly, by setting TraceOff->oform, you can specify that tracing should be switched off during the evaluation of forms that match oform.
| Trace[expr,lhs->rhs] | find all expressions matching lhs that arise during the evaluation of expr, and replace them with rhs |
A powerful aspect of the Wolfram System Trace function is that the object it returns is basically a standard Wolfram System expression that you can manipulate using other Wolfram System functions. One important point to realize, however, is that Trace wraps all expressions that appear in the list it produces with HoldForm to prevent them from being evaluated. The HoldForm is not displayed in standard Wolfram System output format, but it is still present in the internal structure of the expression.
The expressions are wrapped with HoldForm to prevent them from evaluating:
In standard Wolfram System output format, it is sometimes difficult to tell which lists are associated with the structure returned by Trace, and which are expressions being evaluated:
When you use a transformation rule in Trace, the result is evaluated before being wrapped with HoldForm:
For sophisticated computations, the list structures returned by Trace can be quite complicated. When you use Trace[expr,form], Trace will include as elements in the lists only those expressions that match the pattern form. But whatever pattern you give, the nesting structure of the lists remains the same.
You can set the option TraceDepth->n to tell Trace to include only lists nested at most n levels deep. In this way, you can often pick out the "big steps" in a computation, without seeing the details. Note that by setting TraceDepth or TraceOff you can avoid looking at many of the steps in a computation, and thereby significantly speed up the operation of Trace for that computation.
| Trace[expr,form,TraceDepth->n] | trace the evaluation of expr, ignoring steps that lead to lists nested more than n levels deep |
When you use Trace[expr,form], you get a list of all the expressions that match form produced during the evaluation of expr. Sometimes it is useful to see not only these expressions, but also the results that were obtained by evaluating them. You can do this by setting the option TraceForward->True in Trace.
This shows not only expressions that match fac[_], but also the results of evaluating those expressions:
Expressions picked out using Trace[expr,form] typically lie in the middle of an evaluation chain. By setting TraceForward->True, you tell Trace to include also the expression obtained at the end of the evaluation chain. If you set TraceForward->All, Trace will include all the expressions that occur after the expression matching form on the evaluation chain.
With TraceForward->All, all elements on the evaluation chain after the one that matches fac[_] are included:
By setting the option TraceForward, you can effectively see what happens to a particular form of expression during an evaluation. Sometimes, however, you want to find out not what happens to a particular expression, but instead how that expression was generated. You can do this by setting the option TraceBackward. What TraceBackward does is to show you what preceded a particular form of expression on an evaluation chain.
TraceForward and TraceBackward allow you to look forward and backward in a particular evaluation chain. Sometimes, you may also want to look at the evaluation chains within which the particular evaluation chain occurs. You can do this using TraceAbove. If you set the option TraceAbove->True, then Trace will include the initial and final expressions in all the relevant evaluation chains. With TraceAbove->All, Trace includes all the expressions in all these evaluation chains.
This includes the initial and final expressions in all evaluation chains that contain the chain that contains 120:
| Trace[expr,form,opts] | trace the evaluation of expr using the specified options |
| TraceForward->True | include the final expression in the evaluation chain containing form |
| TraceForward->All | include all expressions following form in the evaluation chain |
| TraceBackward->True | include the first expression in the evaluation chain containing form |
| TraceBackward->All | include all expressions preceding form in the evaluation chain |
| TraceAbove->True | include the first and last expressions in all evaluation chains that contain the chain containing form |
| TraceAbove->All | include all expressions in all evaluation chains that contain the chain containing form |
The basic way that Trace[expr,…] works is to intercept each expression encountered during the evaluation of expr, and then to use various criteria to determine whether this expression should be recorded. Normally, however, Trace intercepts expressions only after function arguments have been evaluated. By setting TraceOriginal->True, you can get Trace also to look at expressions before function arguments have been evaluated.
The list structure produced by Trace normally includes only expressions that constitute steps in non‐trivial evaluation chains. Thus, for example, individual symbols that evaluate to themselves are not normally included. Nevertheless, if you set TraceOriginal->True, then Trace looks at absolutely every expression involved in the evaluation process, including those that have trivial evaluation chains.
In this case, Trace includes absolutely all expressions, even those with trivial evaluation chains:
option name | default value | |
| TraceForward | False | whether to show expressions following form in the evaluation chain |
| TraceBackward | False | whether to show expressions preceding form in the evaluation chain |
| TraceAbove | False | whether to show evaluation chains leading to the evaluation chain containing form |
| TraceOriginal | False | whether to look at expressions before their heads and arguments are evaluated |
Additional options for Trace.
When you use Trace to study the execution of a program, there is an issue about how local variables in the program should be treated. As discussed in "How Modules Work", Wolfram System scoping constructs such as Module create symbols with new names to represent local variables. Thus, even if you called a variable x in the original code for your program, the variable may effectively be renamed x$nnn when the program is executed.
Trace[expr,form] is set up so that by default a symbol x that appears in form will match all symbols with names of the form x$nnn that arise in the execution of expr. As a result, you can for example use Trace[expr,x=_] to trace assignment to all variables, local and global, that were named x in your original program.
| Trace[expr,form,MatchLocalNames->False] | |
include all steps in the execution of expr that match form, with no replacements for local variable names allowed | |
In some cases, you may want to trace only the global variable x, and not any local variables that were originally named x. You can do this by setting the option MatchLocalNames->False.
The function Trace performs a complete computation, then returns a structure that represents the history of the computation. Particularly in very long computations, it is however sometimes useful to see traces of the computation as it proceeds. The function TracePrint works essentially like Trace, except that it prints expressions when it encounters them, rather than saving up all of the expressions to create a list structure.
The sequence of expressions printed by TracePrint corresponds to the sequence of expressions given in the list structure returned by Trace. Indentation in the output from TracePrint corresponds to nesting in the list structure from Trace. You can use the Trace options TraceOn, TraceOff and TraceForward in TracePrint. However, since TracePrint produces output as it goes, it cannot support the option TraceBackward. In addition, TracePrint is set up so that TraceOriginal is effectively always set to True.
| Trace[expr,…] | trace the evaluation of expr, returning a list structure containing the expressions encountered |
| TracePrint[expr,…] | trace the evaluation of expr, printing the expressions encountered |
| TraceDialog[expr,…] | trace the evaluation of expr, initiating a dialog when each specified expression is encountered |
| TraceScan[f,expr,…] |
The function TraceDialog effectively allows you to stop in the middle of a computation and interact with the Wolfram System environment that exists at that time. You can, for example, find values of intermediate variables in the computation, and even reset those values. There are, however, a number of subtleties, mostly associated with pattern and module variables.
What TraceDialog does is to call the function Dialog on a sequence of expressions. The Dialog function is discussed in detail in "Dialogs". When you call Dialog, you are effectively starting a subsidiary Wolfram System session with its own sequence of input and output lines.
In general, you may need to apply arbitrary functions to the expressions you get while tracing an evaluation. TraceScan[f,expr,…] applies f to each expression that arises. The expression is wrapped with HoldForm to prevent it from evaluating.
In TraceScan[f,expr,…], the function f is applied to expressions before they are evaluated. TraceScan[f,expr,patt,fp] applies f before evaluation, and fp after evaluation.
Throughout any computation, the Wolfram System maintains an evaluation stack containing the expressions it is currently evaluating. You can use the function Stack to look at the stack. This means, for example, that if you interrupt the Wolfram System in the middle of a computation, you can use Stack to find out what the Wolfram System is doing.
The expression that the Wolfram System most recently started to evaluate always appears as the last element of the evaluation stack. The previous elements of the stack are the other expressions whose evaluation is currently in progress.
Thus at the point when x is being evaluated, the stack associated with the evaluation of an expression like f[g[x]] will have the form {f[g[x]],g[x],x}.
Stack[_] gives the expressions that are being evaluated at the time when it is called, in this case including the Print function:
Stack[] gives the tags associated with the evaluations that are being done when it is called:
In general, you can think of the evaluation stack as showing what functions called what other functions to get to the point the Wolfram System is at in your computation. The sequence of expressions corresponds to the first elements in the successively nested lists returned by Trace with the option TraceAbove set to True.
| Stack[] | give a list of the tags associated with evaluations that are currently being done |
| Stack[_] | give a list of all expressions currently being evaluated |
| Stack[form] | include only expressions which match form |
It is rather rare to call Stack directly in your main Wolfram System session. More often, you will want to call Stack in the middle of a computation. Typically, you can do this from within a dialog, or subsidiary session, as discussed in "Dialogs".
In the simplest cases, the Wolfram System evaluation stack is set up to record all expressions currently being evaluated. Under some circumstances, however, this may be inconvenient. For example, executing Print[Stack[]] will always show a stack with Print as the last function.
The function StackInhibit allows you to avoid this kind of problem. StackInhibit[expr] evaluates expr without modifying the stack.
Functions like TraceDialog automatically call StackInhibit each time they start a dialog. This means that Stack does not show functions that are called within the dialog, only those outside.
| StackInhibit[expr] | evaluate expr without modifying the stack |
| StackBegin[expr] | evaluate expr with a fresh stack |
| StackComplete[expr] | evaluate expr with intermediate expressions in evaluation chains included on the stack |
By using StackInhibit and StackBegin, you can control which parts of the evaluation process are recorded on the stack. StackBegin[expr] evaluates expr, starting a fresh stack. This means that during the evaluation of expr, the stack does not include anything outside the StackBegin. Functions like TraceDialog[expr,…] call StackBegin before they begin evaluating expr, so that the stack shows how expr is evaluated, but not how TraceDialog was called.
Stack normally shows you only those expressions that are currently being evaluated. As a result, it includes only the latest form of each expression. Sometimes, however, you may find it useful also to see earlier forms of the expressions. You can do this using StackComplete.
What StackComplete[expr] effectively does is to keep on the stack the complete evaluation chain for each expression that is currently being evaluated. In this case, the stack corresponds to the sequence of expressions obtained from Trace with the option TraceBackward->All as well as TraceAbove->True.
The general principle that the Wolfram Language follows in evaluating expressions is to go on applying transformation rules until the expressions no longer change. This means, for example, that if you make an assignment like x=x+1, the Wolfram Language should go into an infinite loop. In fact, the Wolfram Language stops after a definite number of steps, determined by the value of the global variable $RecursionLimit. You can always stop the Wolfram Language earlier by explicitly interrupting it.
This assignment could cause an infinite loop. The Wolfram Language stops after a number of steps determined by $RecursionLimit:
| $RecursionLimit | maximum depth of the evaluation stack |
| $IterationLimit | maximum length of an evaluation chain |
Here is a circular definition, whose evaluation is stopped by $IterationLimit:
The variables $RecursionLimit and $IterationLimit control the two basic ways that an evaluation can become infinite in the Wolfram Language. $RecursionLimit limits the maximum depth of the evaluation stack, or equivalently, the maximum nesting depth that would occur in the list structure produced by Trace. $IterationLimit limits the maximum length of any particular evaluation chain, or the maximum length of any single list in the structure produced by Trace.
$RecursionLimit and $IterationLimit are by default set to values that are appropriate for most computations, and most computer systems. You can, however, reset these variables to any integer (above a lower limit), or to Infinity. Note that on most computer systems, you should never set $RecursionLimit=Infinity, as discussed in "Memory Management".
The variable i was incremented to 37 rather than 40 as CompoundExpression, t and Plus are also in the evaluation chain:
In this case, no complicated structure is built up, and the computation is stopped by $IterationLimit:
It is important to realize that infinite loops can take up not only time but also computer memory. Computations limited by $IterationLimit do not normally build up large intermediate structures. But those limited by $RecursionLimit often do. In many cases, the size of the structures produced is a linear function of the value of $RecursionLimit. But in some cases, the size can grow exponentially, or worse, with $RecursionLimit.
An assignment like x=x+1 is obviously circular. When you set up more complicated recursive definitions, however, it can be much more difficult to be sure that the recursion terminates, and that you will not end up in an infinite loop. The main thing to check is that the right‐hand sides of your transformation rules will always be different from the left‐hand sides. This ensures that evaluation will always "make progress", and the Wolfram Language will not simply end up applying the same transformation rule to the same expression over and over again.
Some of the trickiest cases occur when you have rules that depend on complicated /; conditions (see "Putting Constraints on Patterns"). One particularly awkward case is when the condition involves a "global variable". The Wolfram Language may think that the evaluation is finished because the expression did not change. However, a side effect of some other operation could change the value of the global variable, and so should lead to a new result in the evaluation. The best way to avoid this kind of difficulty is not to use global variables in /; conditions. If all else fails, you can type Update[s] to tell the Wolfram Language to update all expressions involving s. Update[] tells the Wolfram Language to update absolutely all expressions.
"Interrupting Calculations" describes how you can interrupt a Wolfram Language computation by pressing appropriate keys on your keyboard.
In some cases, you may want to simulate such interrupts from within a Wolfram Language program. In general, executing Interrupt[] has the same effect as pressing interrupt keys. On a typical system, a menu of options is displayed, as discussed in "Interrupting Calculations".
| Interrupt[] | interrupt a computation |
| Abort[] | abort a computation |
| CheckAbort[expr,failexpr] | evaluate expr and return the result, or failexpr if an abort occurs |
| AbortProtect[expr] | evaluate expr, masking the effect of aborts until the evaluation is complete |
The function Abort[] has the same effect as interrupting a computation, and selecting the abort option in the interrupt menu.
You can use Abort[] to implement an "emergency stop" in a program. In almost all cases, however, you should try to use functions like Return and Throw, which lead to more controlled behavior.
If you abort at any point during the evaluation of a Wolfram Language expression, the Wolfram Language normally abandons the evaluation of the whole expression, and returns the value $Aborted.
You can, however, "catch" aborts using the function CheckAbort. If an abort occurs during the evaluation of expr in CheckAbort[expr,failexpr], then CheckAbort returns failexpr, but the abort propagates no further. Functions like Dialog use CheckAbort in this way to contain the effect of aborts.
When you construct sophisticated programs in the Wolfram Language, you may sometimes want to guarantee that a particular section of code in a program cannot be aborted, either interactively or by calling Abort. The function AbortProtect allows you to evaluate an expression, saving up any aborts until after the evaluation of the expression is complete.
The CheckAbort sees the abort, but does not propagate it further:
Even inside AbortProtect, CheckAbort will see any aborts that occur, and will return the appropriate failexpr. Unless this failexpr itself contains Abort[], the aborts will be "absorbed" by the CheckAbort.
If you make a definition like f[x_]:=x Sin[x], the Wolfram Language will store the expression x Sin[x] in a form that can be evaluated for any x. Then when you give a particular value for x, the Wolfram Language substitutes this value into x Sin[x], and evaluates the result. The internal code that the Wolfram Language uses to perform this evaluation is set up to work equally well whether the value you give for x is a number, a list, an algebraic object, or any other kind of expression.
Having to take account of all these possibilities inevitably makes the evaluation process slower. However, if the Wolfram Language could assume that x will be a machine number, then it could avoid many steps, and potentially evaluate an expression like x Sin[x] much more quickly.
Using Compile, you can construct compiled functions in the Wolfram Language, which evaluate Wolfram Language expressions assuming that all the parameters which appear are numbers (or logical variables). Compile[{x1,x2,…},expr] takes an expression expr and returns a "compiled function" which evaluates this expression when given arguments 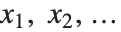 .
.
In general, Compile creates a CompiledFunction object which contains a sequence of simple instructions for evaluating the compiled function. The instructions are chosen to be close to those found in the machine code of a typical computer, and can thus be executed quickly.
| Compile[{x1,x2,…},expr] | create a compiled function which evaluates expr for numerical values of the xi |
This creates a compiled function for evaluating x Sin[x]:
Compile is useful in situations where you have to evaluate a particular numerical or logical expression many times. By taking the time to call Compile, you can get a compiled function which can be executed more quickly than an ordinary Wolfram Language function.
For simple expressions such as x Sin[x], there is usually little difference between the execution speed for ordinary and compiled functions. However, as the size of the expressions involved increases, the advantage of compilation also increases. For large expressions, compilation can speed up execution by a factor as large as 20.
Compilation makes the biggest difference for expressions containing a large number of simple, say arithmetic, functions. For more complicated functions, such as BesselK or Eigenvalues, most of the computation time is spent executing internal Wolfram Language algorithms, on which compilation has no effect.
This creates a compiled function for finding values of the tenth Legendre polynomial. Evaluate tells the Wolfram Language to construct the polynomial explicitly before doing compilation:
Even though you can use compilation to speed up numerical functions that you write, you should still try to use built‐in Wolfram Language functions whenever possible. Built‐in functions will usually run faster than any compiled Wolfram Language programs you can create. In addition, they typically use more extensive algorithms, with more complete control over numerical precision and so on.
You should realize that built‐in Wolfram Language functions quite often themselves use Compile. Thus, for example, NIntegrate by default automatically uses Compile on the expression you tell it to integrate. Similarly, functions like Plot and Plot3D use Compile on the expressions you ask them to plot. Built‐in functions that use Compile typically have the option Compiled. Setting Compiled->False tells the functions not to use Compile.
| Compile[{{x1,t1},{x2,t2},…},expr] | compile expr assuming that xi is of type ti |
| Compile[{{x1,t1,n1},{x2,t2,n2},…},expr] | |
compile expr assuming that xi is a rank ni array of objects each of type ti | |
| Compile[vars,expr,{{p1,pt1},…}] | compile expr, assuming that subexpressions which match pi are of type pti |
| _Integer | machine‐size integer |
| _Real | machine‐precision approximate real number |
| _Complex | machine‐precision approximate complex number |
| True|False | logical variable |
Compile works by making assumptions about the types of objects that occur in evaluating the expression you give. The default assumption is that all variables in the expression are approximate real numbers.
Compile nevertheless also allows integers, complex numbers and logical variables (True or False), as well as arrays of numbers. You can specify the type of a particular variable by giving a pattern which matches only values that have that type. Thus, for example, you can use the pattern _Integer to specify the integer type. Similarly, you can use True|False to specify a logical variable that must be either True or False.
The types that Compile handles correspond essentially to the types that computers typically handle at a machine‐code level. Thus, for example, Compile can handle approximate real numbers that have machine precision, but it cannot handle arbitrary‐precision numbers. In addition, if you specify that a particular variable is an integer, Compile generates code only for the case when the integer is of "machine size", typically between  .
.
When the expression you ask to compile involves only standard arithmetic and logical operations, Compile can deduce the types of objects generated at every step simply from the types of the input variables. However, if you call other functions, Compile will typically not know what type of value they return. If you do not specify otherwise, Compile assumes that any other function yields an approximate real number value. You can, however, also give an explicit list of patterns, specifying what type to assume for an expression that matches a particular pattern.
The idea of Compile is to create a function which is optimized for certain types of arguments. Compile is nevertheless set up so that the functions it creates work with whatever types of arguments they are given. When the optimization cannot be used, a standard Wolfram Language expression is evaluated to find the value of the function.
The compiled code cannot be used, so the Wolfram Language prints a warning, then just evaluates the original symbolic expression:
The compiled code generated by Compile must make assumptions not only about the types of arguments you will supply, but also about the types of all objects that arise during the execution of the code. Sometimes these types depend on the actual values of the arguments you specify. Thus, for example, Sqrt[x] yields a real number result for real x if x is not negative, but yields a complex number if x is negative.
Compile always makes a definite assumption about the type returned by a particular function. If this assumption turns out to be invalid in a particular case when the code generated by Compile is executed, then the Wolfram Language simply abandons the compiled code in this case, and evaluates an ordinary Wolfram Language expression to get the result.
The compiled code does not expect a complex number, so the Wolfram Language has to revert to explicitly evaluating the original symbolic expression:
An important feature of Compile is that it can handle not only mathematical expressions, but also various simple Wolfram Language programs. Thus, for example, Compile can handle conditionals and control flow structures.
In all cases, Compile[vars,expr] holds its arguments unevaluated. This means that you can explicitly give a "program" as the expression to compile.