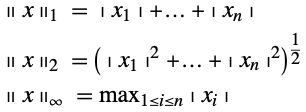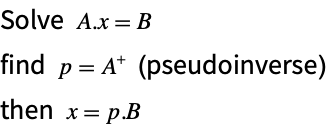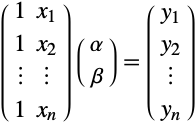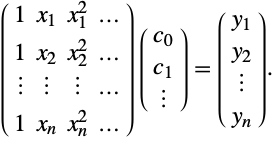-
Functions
- CharacteristicPolynomial
- CholeskyDecomposition
- Det
- Eigensystem
- Eigenvalues
- Eigenvectors
- Inverse
- JordanDecomposition
- LinearSolve
- LUDecomposition
- MatrixExp
- MatrixPower
- MatrixRank
- Minors
- Norm
- NullSpace
- Orthogonalize
- PseudoInverse
- QRDecomposition
- RowReduce
- SchurDecomposition
- SingularValueDecomposition
- SingularValueList
- Related Guides
-
-
Functions
- CharacteristicPolynomial
- CholeskyDecomposition
- Det
- Eigensystem
- Eigenvalues
- Eigenvectors
- Inverse
- JordanDecomposition
- LinearSolve
- LUDecomposition
- MatrixExp
- MatrixPower
- MatrixRank
- Minors
- Norm
- NullSpace
- Orthogonalize
- PseudoInverse
- QRDecomposition
- RowReduce
- SchurDecomposition
- SingularValueDecomposition
- SingularValueList
- Related Guides
-
Functions
Matrix Computations
| Basic Operations | Eigensystem Computations |
| Solving Linear Systems | Matrix Decompositions |
| Least Squares Solutions | Functions of Matrices |
This tutorial reviews the functions that Wolfram Language provides for carrying out matrix computations. Further information on these functions can be found in standard mathematical texts by such authors as Golub and van Loan or Meyer. The operations described in this tutorial are unique to matrices; an exception is the computation of norms, which also extends to scalars and vectors.
Basic Operations
This section gives a review of some basic concepts and operations that will be used throughout the tutorial to discuss matrix operations.
Norms
The norm of a mathematical object is a measurement of the length, size, or extent of the object. In Wolfram Language norms are available for scalars, vectors, and matrices.
| Norm[num] | norm of a number |
| Norm[vec] | 2‐norm of a vector |
| Norm[vec,p] | p‐norm of a vector |
| Norm[mat] | 2‐norm of a matrix |
| Norm[mat,p] | p‐norm of a matrix |
| Norm[mat,"Frobenius"] | Frobenius norm of a matrix |
Computing norms in Wolfram Language.
Vector Norms
For vector spaces, norms allow a measure of distance. This allows the definition of many familiar concepts such as neighborhood, closeness of approximation, and goodness of fit. A vector norm is a function ![]() that satisfies the following relations.
that satisfies the following relations.
Typically this function uses the notation ![]() . The subscript is used to distinguish different norms, of which the p-norms are particularly important. For
. The subscript is used to distinguish different norms, of which the p-norms are particularly important. For ![]() , the p-norm is defined as follows.
, the p-norm is defined as follows.
Some common p-norms are the 1-, 2-, and ![]() -norms.
-norms.
Matrix Norms
Matrix norms are used to give a measure of distance in matrix spaces. This is necessary if you want to quantify what it means for one matrix to be near to another, for example, to say that a matrix is nearly singular.
Matrix norms also use the double bar notation of vector norms. One of the most common matrix norms is the Frobenius norm (also called the Euclidean norm).
Other common norms are the p-norms. These are defined in terms of vector p-norms as follows.
Thus the matrix p-norms show the maximum expansion that a matrix can apply to any vector.
NullSpace
One of the fundamental subspaces associated with each matrix is the null space. Vectors in the null space of a matrix are mapped to zero by the action of the matrix.
| NullSpace[m] | a list of basis vectors whose linear combinations satisfy |
Rank
The rank of a matrix corresponds to the number of linearly independent rows or columns in the matrix.
| MatrixRank[mat] | give the rank of the matrix mat |
For an m×n matrix A the following relations hold: Length[NullSpace[A]]+ MatrixRank[A]n, and Length[NullSpace[AT]]+ MatrixRank[AT]m. From this it follows that the null space is empty if and only if the rank is equal to n and that the null space of the transpose of A is empty if and only if the rank of A is equal to m.
If the rank is equal to the number of columns, it is said to have full column rank. If the rank is equal to the number of rows, it is said to have full row rank. One way to understand the rank of a matrix is to consider the row echelon form.
Reduced Row Echelon Form
A matrix can be reduced to a row echelon form by a combination of row operations that start with a pivot position at the top-left element and subtract multiples of the pivot row from following rows so that all entries in the column below the pivot are zero. The next pivot is chosen by going to the next row and column. If this pivot is zero and any nonzero entries are in the column beneath, the rows are exchanged and the process is repeated. The process finishes when the last row or column is reached.
A matrix is in row echelon form if any row that consists entirely of zeros is followed only by other zero rows and if the first nonzero entry in row ![]() is in the column
is in the column ![]() , then elements in columns from 1 to
, then elements in columns from 1 to ![]() in all rows below
in all rows below ![]() are zero. The row echelon form is not unique but its form (in the sense of the positions of the pivots) is unique. It also gives a way to determine the rank of a matrix as the number of nonzero rows.
are zero. The row echelon form is not unique but its form (in the sense of the positions of the pivots) is unique. It also gives a way to determine the rank of a matrix as the number of nonzero rows.
A matrix is in reduced row echelon form if it is in row echelon form, each pivot is one, and all the entries above (and below) each pivot are zero. It can be formed by a procedure similar to the procedure for the row echelon form, also taking steps to reduce the pivot to one (by division) and reduce entries in the column above each pivot to zero (by subtracting multiples of the current pivot row). The reduced row echelon form of a matrix is unique.
The reduced row echelon form (and row echelon form) give a way to determine the rank of a matrix as the number of nonzero rows. In Wolfram Language the reduced row echelon form of a matrix can be computed by the function RowReduce.
| RowReduce[mat] | give the reduced row echelon form of the matrix mat |
Inverse
The inverse of a square matrix A is defined by
where ![]() is the identity matrix. The inverse can be computed in Wolfram Language with the function Inverse.
is the identity matrix. The inverse can be computed in Wolfram Language with the function Inverse.
| Inverse[mat] | give the inverse of the matrix mat |
The matrix inverse can in principle be used to solve the matrix equation
by multiplying it by the inverse of ![]() .
.
However, it is always better to solve the matrix equation directly. Such techniques are discussed in the section "Solving Linear Systems".
PseudoInverse
When the matrix is singular or is not square it is still possible to find an approximate inverse that minimizes ![]() . When the 2-norm is used this will find a least squares solution known as the pseudoinverse.
. When the 2-norm is used this will find a least squares solution known as the pseudoinverse.
| PseudoInverse[mat] | give the pseudoinverse of the matrix mat |
The solution found by the pseudoinverse is a least squares solution. These are discussed in more detail under "Least Squares Solutions".
Determinant
The determinant of an n×n matrix is defined as follows.
It can be computed in Wolfram Language with the function Det.
| Det[mat] | determinant of the matrix mat |
| Minors[mat] | matrix of minors of mat |
| Minors[mat,k] | k th minors of mat |
Minors
Solving Linear Systems
One of the most important uses of matrices is to represent and solve linear systems. This section discusses how to solve linear systems with Wolfram Language. It makes strong use of LinearSolve, the main function provided for this purpose.
Solving a linear system involves solving a matrix equation ![]() . Because
. Because ![]() is an
is an ![]() ×
×![]() matrix this is a set of
matrix this is a set of ![]() linear equations in
linear equations in ![]() unknowns.
unknowns.
When ![]() the system is said to be square. If
the system is said to be square. If ![]() there are more equations than unknowns and the system is overdetermined. If
there are more equations than unknowns and the system is overdetermined. If ![]() there are fewer equations than unknowns and the system is underdetermined.
there are fewer equations than unknowns and the system is underdetermined.
square | m=n; solution may or may not exist |
overdetermined | m>n; solutions may or may not exist |
underdetermined | m<n; no solutions or infinitely many solutions exist |
nonsingular | number of independent equations equal to the number of variables and determinant nonzero; a unique solution exists |
consistent | at least one solution exists |
inconsistent | no solutions exist |
Classes of linear systems represented by rectangular matrices.
Note that even though you could solve the matrix equation by computing the inverse via ![]() , this is not a recommended method. You should use a function that is designed to solve linear systems directly and in Wolfram Language this is provided by LinearSolve.
, this is not a recommended method. You should use a function that is designed to solve linear systems directly and in Wolfram Language this is provided by LinearSolve.
| LinearSolve[m,b] | a vector x that solves the matrix equation m.x==b |
| LinearSolve[m] | a function that can be applied repeatedly to many b |
Solving linear systems with LinearSolve.
If no solution can be found, the system is inconsistent. In this case it might still be useful to find a best-fit solution. This is often done with a least squares technique, which is explored under "Least Squares Solutions".
option name | default value | |
| Method | Automatic | the method to use for solving |
| Modulus | 0 | take the equation to be modulo n |
| ZeroTest | (#0&) | the function to be used by symbolic methods for testing for zero |
Options for LinearSolve.
LinearSolve has three options that allow users more control. The Modulus and ZeroTest options are used by symbolic techniques and are discussed in the section "Symbolic and Exact Matrices". The Method option allows you to choose methods that are known to be suitable for a particular problem; the default setting of Automatic means that LinearSolve chooses a method based on the input.
Singular Matrices
In those cases where a solution cannot be found, it is still possible to find a solution that makes a best fit to the problem. One important class of best-fit solutions involves least squares solutions and is discussed in "Least Squares Solutions".
Homogeneous Equations
The homogeneous matrix equation involves a zero right-hand side.
This equation has a nonzero solution if the matrix is singular. To test if a matrix is singular, you can compute the determinant.
Estimating and Calculating Accuracy
An important way to quantify the accuracy of the solution of a linear system is to compute the condition number ![]() . This is defined as follows for a suitable choice of norm.
. This is defined as follows for a suitable choice of norm.
It can be shown that for the matrix equation ![]() the relative error in
the relative error in ![]() is
is ![]() times the relative error in
times the relative error in ![]() and
and ![]() . Thus, the condition number quantifies the accuracy of the solution. If the condition number of a matrix is large, the matrix is said to be ill-conditioned. You cannot expect a good solution from an ill-conditioned system. For some extremely ill-conditioned systems it is not possible to obtain any solution.
. Thus, the condition number quantifies the accuracy of the solution. If the condition number of a matrix is large, the matrix is said to be ill-conditioned. You cannot expect a good solution from an ill-conditioned system. For some extremely ill-conditioned systems it is not possible to obtain any solution.
In Wolfram Language an approximation of the condition number can be computed with the function LinearAlgebra`MatrixConditionNumber.
| LinearAlgebra`MatrixConditionNumber[mat] | |
| infinity‐norm approximate condition number of a matrix of approximate numbers | |
| LinearAlgebra`MatrixConditionNumber[mat,Norm->p] | |
| p‐norm approximate condition number of a matrix, where p may be 1, 2, or | |
Symbolic and Exact Matrices
LinearSolve works for all the different types of matrices that can be represented in Wolfram Language. These are described in more detail in "Matrix Types".
In order to simplify the intermediate expressions, the ZeroTest option might be useful.
There are a number of methods that are specific to symbolic and exact computation: CofactorExpansion, DivisionFreeRowReduction, and OneStepRowReduction. These are discussed in the section "Symbolic Methods".
Row Reduction
Saving the Factorization
The one-argument form of LinearSolve works in a completely equivalent way to the two-argument form. It works with the same range of input matrices, for example, returning the expected results for symbolic, exact, or sparse matrix input. It also accepts the same options.
Methods
LinearSolve provides a number of different techniques to solve matrix equations that are specialized to particular problems. You can select between these using the option Method. In this way a uniform interface is provided to all the functionality that Wolfram Language provides for solving matrix equations.
The default setting of the option Method is Automatic. As is typical for Wolfram Language, this means that the system will make an automatic choice of method to use. For LinearSolve if the input matrix is numerical and dense, then a method using LAPACK routines is used; if it is numerical and sparse, a multifrontal direct solver is used. If the matrix is symbolic then specialized symbolic routines are used.
The details of the different methods are now described.
LAPACK
LAPACK is the default method for solving dense numerical matrices. When the matrix is square and nonsingular the routines dgesv, dlange, and dgecon are used for real matrices and zgesv, zlange, and zgecon for complex matrices. When the matrix is nonsquare or singular dgelss is used for real matrices and zgelss for complex matrices. More information on LAPACK is available in the references.
If the input matrix uses arbitrary-precision numbers, then LAPACK algorithms extended for arbitrary-precision computation are used.
Multifrontal
The multifrontal method is a direct solver used by default if the input matrix is sparse; it can also be selected by specifying a method option.
If the input matrix to the multifrontal method is dense, it is converted to a sparse matrix.
The implementation of the multifrontal method uses the "UMFPACK" library.
Krylov
The Krylov method is an iterative solver that is suitable for large sparse linear systems, such as those arising from numerical solving of PDEs. In Wolfram Language two Krylov methods are implemented: conjugate gradient (for symmetric positive definite matrices) and BiCGSTAB (for nonsymmetric systems). It is possible to set the method that is used and a number of other parameters by using appropriate suboptions.
option name | default value | |
| MaxIterations | Automatic | the maximum number of iterations |
| Method | BiCGSTAB | the method to use for solving |
| Preconditioner | None | the preconditioner |
| ResidualNormFunction | Automatic | the norm to minimize |
| Tolerance | Automatic | the tolerance to use to terminate the iteration |
Suboptions of the Krylov method.
The default method for Krylov, BiCGSTAB, is more expensive but more generally applicable. The conjugate gradient method is suitable for symmetric positive definite systems, always converging to a solution (though the convergence may be slow). If the matrix is not symmetric positive definite, the conjugate gradient may not converge to a solution.
At present, only the ILU preconditioner is built-in. You can still define your own preconditioner by defining a function that is applied to the input matrix. An example that involves solving a diagonal matrix is shown next.
Generally, a problem will not be structured so that it can benefit so much from such a simple preconditioner. However, this example is useful since it shows how to create and use your own preconditioner.
If the input matrix to the Krylov method is dense, the result is still found because the method is based on matrix/vector multiplication.
The Krylov method can be used to solve systems that are too large for a direct solver. However, it is not a general solver, being particularly suitable for those problems that have some form of diagonal dominance.
Cholesky
For dense matrices the Cholesky method uses LAPACK functions such as dpotrf and dpotrs for real matrices and zpotrf and zpotrs for complex matrices. For sparse matrices the Cholesky method uses the "TAUCS" library.
Symbolic Methods
Least Squares Solutions
In these cases it is possible to find a best-fit solution that minimizes ![]() . A particularly common choice of p is 2; this generates a least squares solution. These are often used because the function
. A particularly common choice of p is 2; this generates a least squares solution. These are often used because the function ![]() is differentiable in
is differentiable in ![]() and because the 2-norm is preserved under orthogonal transformations.
and because the 2-norm is preserved under orthogonal transformations.
If the rank of ![]() is
is ![]() (i.e., it has full column rank), it can be shown (Golub and van Loan) that there is a unique solution to the least squares problem and it solves the linear system.
(i.e., it has full column rank), it can be shown (Golub and van Loan) that there is a unique solution to the least squares problem and it solves the linear system.
These are called the normal equations. Although they can be solved directly to get a least squares solution, this is not recommended because if the matrix ![]() is ill-conditioned then the product
is ill-conditioned then the product ![]() will be even more ill-conditioned. Ways of finding least squares solutions for full rank matrices are explored in "Examples: Full Rank Least Squares Solutions".
will be even more ill-conditioned. Ways of finding least squares solutions for full rank matrices are explored in "Examples: Full Rank Least Squares Solutions".
It should be noted that best-fit solutions that minimize other norms, such as 1 and ![]() , are also possible. A number of ways to find solutions to overdetermined systems that are suitable for special types of matrices or to minimize other norms are given under "Minimization of 1 and Infinity Norms".
, are also possible. A number of ways to find solutions to overdetermined systems that are suitable for special types of matrices or to minimize other norms are given under "Minimization of 1 and Infinity Norms".
A general way to find a least squares solution to an overdetermined system is to use a singular value decomposition to form a matrix that is known as the pseudoinverse of a matrix. In Wolfram Language this is computed with PseudoInverse. This technique works even if the input matrix is rank deficient. The basis of the technique follows.
Data Fitting
Scientific measurements often result in collections of ordered pairs of data, ![]() . In order to make predictions at times other than those that were measured, it is common to try to fit a curve through the data points. If the curve is a straight line, then the aim is to find unknown coefficients
. In order to make predictions at times other than those that were measured, it is common to try to fit a curve through the data points. If the curve is a straight line, then the aim is to find unknown coefficients ![]() and
and ![]() for which
for which
for all the data pairs. This can be written in a matrix form as shown here and is immediately recognized as being equivalent to solving an overdetermined system of linear equations.
Fitting a more general curve, for example,
is equivalent to the matrix equation
In this case the left-hand matrix is a Vandermonde matrix. In fact any function that is linear in the unknown coefficients can be used.
The function FindFit is quite general; it can also fit functions to data that is not linear in the parameters.
Eigensystem Computations
The solution of the eigenvalue problem is one of the major areas for matrix computations. It has many applications in physics, chemistry, and engineering. For an ![]() ×
×![]() matrix
matrix ![]() the eigenvalues are the
the eigenvalues are the ![]() roots of its characteristic polynomial,
roots of its characteristic polynomial, ![]() . The set of roots,
. The set of roots, ![]() , are called the spectrum of the matrix. For each eigenvalue,
, are called the spectrum of the matrix. For each eigenvalue, ![]() , the vectors,
, the vectors, ![]() , that satisfy
, that satisfy
are described as eigenvectors. The matrix of the eigenvectors, ![]() , if it exists and is nonsingular, may be used as a similarity transformation to form a diagonal matrix with the eigenvalues on the diagonal elements. Many important applications of eigenvalues involve the diagonalization of matrices in this way.
, if it exists and is nonsingular, may be used as a similarity transformation to form a diagonal matrix with the eigenvalues on the diagonal elements. Many important applications of eigenvalues involve the diagonalization of matrices in this way.
Wolfram Language has various functions for computing eigenvalues and eigenvectors.
| Eigenvalues[m] | a list of the eigenvalues of m |
| Eigenvectors[m] | a list of the eigenvectors of m |
| Eigensystem[m] | a list of the form {eigenvalues,eigenvectors} |
| CharacteristicPolynomial[m,x] | the characteristic polynomial of m |
Certain applications of eigenvalues do not require all of the eigenvalues to be computed. Wolfram Language provides a mechanism for obtaining only some eigenvalues.
| Eigenvalues[m,k] | the largest k eigenvalues of m |
| Eigenvectors[m,k] | the corresponding eigenvectors of m |
| Eigenvalues[m,-k] | the smallest k eigenvalues of m |
| Eigenvectors[m,-k] | the corresponding eigenvectors of m |
option name | default value | |
| Cubics | False | whether to return radicals for 3×3 matrices |
| Method | Automatic | the method to use for solving |
| Quartics | False | whether to return radicals for 4×4 matrices |
| ZeroTest | (#0&) | the function to be used by symbolic methods for testing for zero |
Options for Eigensystem.
Eigensystem has four options that allow users more control. The Cubics, Quartics, and ZeroTest options are used by symbolic techniques and are discussed under "Symbolic and Exact Matrices". The Method option allows knowledgeable users to choose methods that are particularly appropriate for their problems; the default setting of Automatic means that Eigensystem makes a choice of a method that is generally suitable.
Eigensystem Properties
This section describes certain properties of eigensystem computations. It should be remembered that because the eigenvalues of an ![]() ×
×![]() matrix can be associated with the roots of an
matrix can be associated with the roots of an ![]() th degree polynomial, there will always be
th degree polynomial, there will always be ![]() eigenvalues.
eigenvalues.
Diagonalizing a Matrix
Similarity transformations preserve a number of useful properties of a matrix such as determinant, rank, and trace.
Symbolic and Exact Matrices
As is typical for Wolfram Language, if a computation is done for a symbolic or exact matrix it will use symbolic computer algebra techniques and return a symbolic or exact result.
Generalized Eigenvalues
For ![]() ×
×![]() matrices
matrices ![]() the generalized eigenvalues are the
the generalized eigenvalues are the ![]() roots of its characteristic polynomial,
roots of its characteristic polynomial, ![]() . For each generalized eigenvalue,
. For each generalized eigenvalue, ![]() , the vectors,
, the vectors, ![]() , that satisfy
, that satisfy
are described as generalized eigenvectors.
| Eigenvalues[{a,b}] | the generalized eigenvalues of a and b |
| Eigenvectors[{a,b}] | the generalized eigenvectors of a and b |
| Eigensystem[{a,b}] | the generalized eigensystem of a and b |
Generalized eigenvalues and eigenvectors.
Methods
Eigenvalue computations are solved with a number of different techniques that are specialized to particular problems. You can select between these using the option Method. In this way a uniform interface is provided to all the functionality that Wolfram Language provides.
The default setting of the option Method is Automatic. As is typical for Wolfram Language, this means that the system will make an automatic choice of method to use. For eigenvalue computation when the input is an ![]() ×
×![]() matrix of machine numbers and the number of eigenvalues requested is less than 20% of
matrix of machine numbers and the number of eigenvalues requested is less than 20% of ![]() an Arnoldi method is used. Otherwise, if the input matrix is numerical then a method using LAPACK routines is used. If the matrix is symbolic then specialized symbolic routines are used.
an Arnoldi method is used. Otherwise, if the input matrix is numerical then a method using LAPACK routines is used. If the matrix is symbolic then specialized symbolic routines are used.
The details of the different methods are now described.
LAPACK
LAPACK is the default method for computing the entire set of eigenvalues and eigenvectors. When the matrix is unsymmetric, dgeev is used for real matrices and zgeev is used for complex matrices. For symmetric matrices, dsyevr is used for real matrices and zheevr is used for complex matrices. For generalized eigenvalues the routine dggev is used for real matrices and zggev for complex matrices. More information on LAPACK is available in the references section.
If the input matrix uses arbitrary-precision numbers, LAPACK algorithms extended for arbitrary-precision computation are used.
Arnoldi
The Arnoldi method is an iterative method used to compute a finite number of eigenvalues. The implementation of the Arnoldi method uses the "ARPACK" library. The most general problem that can be solved with this technique is to compute a few selected eigenvalues for
Because it is an iterative technique and only finds a few eigenvalues, it is often suitable for sparse matrices. One of the features of the technique is the ability to apply a shift ![]() and solve for a given eigenvector
and solve for a given eigenvector ![]() and eigenvalue
and eigenvalue ![]() (where
(where ![]() ).
).
This is effective for finding eigenvalues near to ![]() .
.
The following suboptions can be given to the Arnoldi method.
option name | default value | |
| BasisSize | Automatic | the size of the Arnoldi basis |
| Criteria | Magnitude | the method to use for solving |
| MaxIterations | Automatic | the maximum number of iterations |
| Shift | None | an Arnoldi shift |
| StartingVector | Automatic | the initial vector to use |
| Tolerance | Automatic | the tolerance to use to terminate the iteration |
Suboptions of the Arnoldi method.

For many large sparse systems that occur in practical computations the Arnoldi algorithm is able to converge quite quickly.
Symbolic Methods
Symbolic eigenvalue computations work by interpolating the characteristic polynomial.
Matrix Decompositions
This section will discuss a number of standard techniques for working with matrices. These are often used as building blocks for solving matrix problems. The decompositions fall into the categories of factorizations, orthogonal transformations, and similarity transformations.
LU Decomposition
The LU decomposition of a matrix is frequently used as part of a Gaussian elimination process for solving a matrix equation. In Wolfram Language there is no need to use an LU decomposition to solve a matrix equation, because the function LinearSolve does this for you, as discussed in the section "Solving Linear Systems". Note that if you want to save the factorization of a matrix, so that it can be used to solve the same left-hand side, you can use the one-argument form of LinearSolve, as demonstrated in the section "Saving the Factorization".
The LU decomposition with partial pivoting of a square nonsingular matrix ![]() involves the computation of the unique matrices
involves the computation of the unique matrices ![]() ,
, ![]() , and
, and ![]() such that
such that
where ![]() is lower triangular with ones on the diagonal,
is lower triangular with ones on the diagonal, ![]() is upper triangular, and
is upper triangular, and ![]() is a permutation matrix. Once it is found, it can be used to solve the matrix equation by finding the solution to the following equivalent system.
is a permutation matrix. Once it is found, it can be used to solve the matrix equation by finding the solution to the following equivalent system.
This can be done by first solving for ![]() in the following.
in the following.
Then solve for ![]() to get the desired solution.
to get the desired solution.
Because both ![]() and
and ![]() are triangular matrices it is particularly easy to solve these systems.
are triangular matrices it is particularly easy to solve these systems.
Despite the fact that in Wolfram Language you do not need to use the LU decomposition for solving matrix equations, Wolfram Language provides the function LUDecomposition for computing the LU decomposition.
| LUDecomposition[m] | the LU decomposition with partial pivoting |
LUDecomposition returns a list of three elements. The first element is a combination of upper and lower triangular matrices, the second element is a vector specifying rows used for pivoting (a permutation vector which is equivalent to the permutation matrix), and the third element is an estimate of the condition number.
One of the features of the LU decomposition is that the lower and upper matrices are stored in the same matrix. The individual ![]() and
and ![]() factors can be obtained as follows. Note how they use a vectorized operation for element-by-element multiplication with a sparse matrix. This makes the process more efficient; these techniques are discussed further in "Programming Efficiency".
factors can be obtained as follows. Note how they use a vectorized operation for element-by-element multiplication with a sparse matrix. This makes the process more efficient; these techniques are discussed further in "Programming Efficiency".
Cholesky Decomposition
The Cholesky decomposition of a symmetric positive definite matrix ![]() is a factorization into a unique upper triangular
is a factorization into a unique upper triangular ![]() such that
such that
This factorization has a number of uses, one of which is that, because it is a triangular factorization, it can be used to solve systems of equations involving symmetric positive definite matrices. (The way that a triangular factorization can be used to solve a matrix equation is shown in the section "LU Decomposition".) If a matrix is known to be of this form it is preferred over the LU factorization because the Cholesky factorization is faster to compute. If you want to solve a matrix equation using the Cholesky factorization you can do this directly from LinearSolve using the Cholesky method; this is described in a previous section.
The Cholesky factorization can be computed in Wolfram Language with the function CholeskyDecomposition.
| CholeskyDecomposition[m] | the Cholesky decomposition |
One way to test if a matrix is positive definite is to see if the Cholesky decomposition exists.
Cholesky and LU Factorizations
The Cholesky factorization is related to the LU factorization as
where ![]() is the diagonal matrix of pivots.
is the diagonal matrix of pivots.
Finally, this computes ![]() ; its transpose is equal to the Cholesky decomposition.
; its transpose is equal to the Cholesky decomposition.
Orthogonalization
Orthogonalization generates an orthonormal basis from an arbitrary basis. An orthonormal basis is a basis, ![]() , for which
, for which
In Wolfram Language a set of vectors can be orthogonalized with the function Orthogonalize.
| Orthogonalize[{v1,v2,…}] | generate an orthonormal set from the given list of real vectors |
By default a Gram–Schmidt orthogonalization is computed, but a number of other orthogonalizations can be computed.
QR Decomposition
The QR decomposition of a rectangular matrix ![]() with linearly independent columns involves the computation of matrices
with linearly independent columns involves the computation of matrices ![]() and
and ![]() such that
such that
where the columns of ![]() form an orthonormal basis for the columns of
form an orthonormal basis for the columns of ![]() and
and ![]() is upper triangular. It can be computed in Wolfram Language with the function QRDecomposition.
is upper triangular. It can be computed in Wolfram Language with the function QRDecomposition.
| QRDecomposition[m] | the QR decomposition of a matrix |
Solving Systems of Equations
For a square nonsingular matrix ![]() the QR decomposition can be used to solve the matrix equation
the QR decomposition can be used to solve the matrix equation ![]() , as is also the case for the LU decomposition. However, when the matrix is rectangular, the QR decomposition is also useful for solving the matrix equation.
, as is also the case for the LU decomposition. However, when the matrix is rectangular, the QR decomposition is also useful for solving the matrix equation.
One particular application of the QR decomposition is to find least squares solutions to overdetermined systems, by solving the system of normal equations
Because ![]() , this can be simplified as
, this can be simplified as
Thus the normal equations simplify to
and because ![]() is nonsingular this simplifies to
is nonsingular this simplifies to
Because ![]() is triangular this is a particularly easy system to solve; sample code to implement this technique is given in "Examples: Least Squares QR".
is triangular this is a particularly easy system to solve; sample code to implement this technique is given in "Examples: Least Squares QR".
Singular Value Decomposition
The singular value decomposition of a rectangular matrix ![]() involves the computation of orthogonal matrices
involves the computation of orthogonal matrices ![]() and
and ![]() and a diagonal matrix
and a diagonal matrix ![]() such that
such that
The diagonal elements of the matrix ![]() are called the singular values of
are called the singular values of ![]() . In Wolfram Language, the function SingularValueList computes the singular values and the function SingularValueDecomposition computes the full singular value decomposition.
. In Wolfram Language, the function SingularValueList computes the singular values and the function SingularValueDecomposition computes the full singular value decomposition.
| SingularValueList[m] | a list of the nonzero singular values of m |
| SingularValueDecomposition[m] | the singular value decomposition of m |
Note that if the matrix is complex, the definition of the singular value decomposition uses the conjugate transpose.
There are many applications of the singular value decomposition. The singular values of a matrix give information on the linear transformation represented by ![]() . For example, the action of
. For example, the action of ![]() on a unit sphere generates an ellipsoid with semi-axes given by the singular values. The singular values can be used to compute the rank of a matrix; the number of nonzero singular values is equal to the rank. The singular values can be used to compute the 2-norm of a matrix, and the columns of the
on a unit sphere generates an ellipsoid with semi-axes given by the singular values. The singular values can be used to compute the rank of a matrix; the number of nonzero singular values is equal to the rank. The singular values can be used to compute the 2-norm of a matrix, and the columns of the ![]() matrix that correspond to zero singular values are the null space of the matrix.
matrix that correspond to zero singular values are the null space of the matrix.
Certain applications of singular values do not require all of the singular values to be computed. Wolfram Language provides a mechanism for obtaining only some singular values.
| SingularValueList[m,k] | the largest k singular values of m |
| SingularValueDecomposition[m,k] | the corresponding singular value decomposition of m |
| SingularValueList[m,-k] | the smallest k singular values of m |
| SingularValueDecomposition[m,-k] | the corresponding singular value decomposition of m |
Generalized Singular Values
For an ![]() ×
×![]() matrix
matrix ![]() and a
and a ![]() ×
×![]() matrix
matrix ![]() the generalized singular values are given by the pair of factorizations
the generalized singular values are given by the pair of factorizations
where ![]() is
is ![]() ×
×![]() ,
, ![]() is
is ![]() ×
×![]() , and
, and ![]() is
is ![]() ×
×![]() ;
; ![]() and
and ![]() are orthogonal, and
are orthogonal, and ![]() is invertible.
is invertible.
| SingularValueList[{a,b}] | the generalized singular values of a and b |
| SingularValueDecomposition[{a,b}] | the generalized singular value decomposition of a and b |
Options
The functions SingularValueList and SingularValueDecomposition both take a Tolerance option.
The option controls the size at which singular values are treated as zero. By default, values that are tol times smaller than the largest singular value are dropped, where tol is 100×$MachineEpsilon for machine-number matrices. For arbitrary-precision matrices, it is ![]() , where
, where ![]() is the precision of the matrix.
is the precision of the matrix.
Schur Decomposition
The Schur decomposition of a square matrix ![]() involves finding a unitary matrix
involves finding a unitary matrix ![]() that can be used for a similarity transformation of
that can be used for a similarity transformation of ![]() to form a block upper triangular matrix
to form a block upper triangular matrix ![]() with 1×1 and 2×2 blocks on the diagonal (the 2×2 blocks correspond to complex conjugate pairs of eigenvalues for a real matrix
with 1×1 and 2×2 blocks on the diagonal (the 2×2 blocks correspond to complex conjugate pairs of eigenvalues for a real matrix ![]() ). A block upper triangular matrix of this form can be called upper quasi-triangular.
). A block upper triangular matrix of this form can be called upper quasi-triangular.
The Schur decomposition always exists and so the similarity transformation of ![]() to upper triangular always exists. This contrasts with the eigensystem similarity transformation, used to diagonalize a matrix, which does not always exist.
to upper triangular always exists. This contrasts with the eigensystem similarity transformation, used to diagonalize a matrix, which does not always exist.
| SchurDecomposition[m] | the Schur decomposition of a matrix |
Generalized Schur Decomposition
For ![]() ×
×![]() matrices
matrices ![]() and
and ![]() , the generalized Schur decomposition is defined as
, the generalized Schur decomposition is defined as
where ![]() and
and ![]() are unitary,
are unitary, ![]() is upper triangular, and
is upper triangular, and ![]() is upper quasi-triangular.
is upper quasi-triangular.
| SchurDecomposition[{a,b}] | the generalized Schur decomposition of a and b |
For real input, a result involving complex numbers and an upper triangular result can be obtained with the option RealBlockForm.
Options
SchurDecomposition takes two options.
option name | default value | |
| Pivoting | False | whether to carry out pivoting and scaling |
| RealBlockForm | True | whether to return 2×2 real blocks for complex eigenvalues |
Options for SchurDecomposition.
The option Pivoting can be used to allow pivoting and scaling to improve the quality of the result. When it is set to True, pivoting and scaling may be used and a matrix ![]() that represents the changes to
that represents the changes to ![]() is returned. With this new matrix the definition of the Schur decomposition can be seen as follows.
is returned. With this new matrix the definition of the Schur decomposition can be seen as follows.
Jordan Decomposition
The Jordan decomposition of a square matrix ![]() involves finding the nonsingular matrix
involves finding the nonsingular matrix ![]() that can be used for a similarity transformation of
that can be used for a similarity transformation of ![]() to generate a matrix
to generate a matrix ![]() (known as the Jordan form) that has a particularly simple triangular structure.
(known as the Jordan form) that has a particularly simple triangular structure.
The Jordan decomposition always exists, but it is hard to compute with floating-point arithmetic. However, computation with exact arithmetic avoids these problems.
| JordanDecomposition[m] | the Jordan decomposition of a matrix |
Functions of Matrices
The computation of functions of matrices is a general problem with applications in many areas such as control theory. The function ![]() of a square matrix
of a square matrix ![]() is not the same as the application of the function to each element in the matrix. Clearly element-wise application would not maintain properties consistent with the application of the function to a scale.
is not the same as the application of the function to each element in the matrix. Clearly element-wise application would not maintain properties consistent with the application of the function to a scale.
There are a number of ways to define functions of matrices; one useful way is to consider a series expansion. For the exponential function this works as follows.
One way to compute this series involves diagonalizing ![]() , so that
, so that ![]() and
and ![]() . Therefore, the exponential of
. Therefore, the exponential of ![]() can be computed as follows.
can be computed as follows.
This technique can be generalized to functions ![]() of the eigenvalues of
of the eigenvalues of ![]() . Note that while this is one way to define functions of matrices, it does not provide a good way to compute them.
. Note that while this is one way to define functions of matrices, it does not provide a good way to compute them.
Wolfram Language does not have a function for computing general functions of matrices, but it has some specific functions.
| MatrixPower[m,n] | n th matrix power |
| MatrixExp[m] | matrix exponential |
| m1.m2 | matrix multiplication |
| Inverse[m] | matrix inverse |
A technique for computing parametrized functions of matrices by solving differential equations is given in "Examples: Matrix Functions with NDSolve".