Orthogonalize[{v1,v2,…}]
gives an orthonormal basis found by orthogonalizing the vectors vi.
Orthogonalize[{e1,e2,…},f]
gives an orthonormal basis found by orthogonalizing the elements ei with respect to the inner product function f.


Orthogonalize
Orthogonalize[{v1,v2,…}]
gives an orthonormal basis found by orthogonalizing the vectors vi.
Orthogonalize[{e1,e2,…},f]
gives an orthonormal basis found by orthogonalizing the elements ei with respect to the inner product function f.
Details and Options

- Orthogonalize[{v1,v2,…}] uses the ordinary scalar product
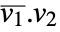 as an inner product.
as an inner product. - The output from Orthogonalize always contains the same number of vectors as the input. If some of the input vectors are not linearly independent, the output will contain zero vectors.
- All nonzero vectors in the output are normalized to unit length.
- The inner product function f is applied to pairs of linear combinations of the ei.
- The ei can be any expressions for which f always yields real results. »
- Orthogonalize[{v1,v2,…},Dot] effectively assumes that all elements of the vi are real. »
- Orthogonalize by default generates a Gram–Schmidt basis.
- Other bases can be obtained by giving alternative settings for the Method option. Possible settings include: "GramSchmidt", "ModifiedGramSchmidt", "Reorthogonalization", and "Householder".
- Orthogonalize[list,Tolerance->t] sets to zero elements whose relative norm falls below t.
Examples
open all close allBasic Examples (3)
Scope (13)
Basic Uses (6)
Special Matrices (4)
Orthogonalize the rows of a sparse matrix:
Orthogonalize the rows of structured matrices:
Orthogonalizing a diagonal matrix produces another diagonal matrix:
Orthogonalize HilbertMatrix:
Options (3)
Method (2)
Applications (12)
Geometry (3)
Project the vector ![]() on the plane spanned by the vectors
on the plane spanned by the vectors ![]() and
and ![]() :
:
Construct an orthonormal basis that spans the same space as the ![]() :
:
The projection in the plane is the sum of the projections onto ![]() :
:
Find the component perpendicular to the plane:
Confirm the result by projecting ![]() onto the normal to the plane:
onto the normal to the plane:
Visualize the plane, the vector and its parallel and perpendicular components:
The Frenet–Serret system encodes every space curve's properties in a vector basis and scalar functions. Consider the following curve:
Construct an orthonormal basis from the first three derivatives using Orthogonalize:
Ensure that the basis is right-handed:
Compute the curvature, ![]() , and torsion,
, and torsion, ![]() , which quantify how the curve bends:
, which quantify how the curve bends:
Verify the answers using FrenetSerretSystem:
Visualize the curve and the associated moving basis, also called a frame:
Find the orthogonal projection of the vector ![]() onto the space spanned by the vectors
onto the space spanned by the vectors ![]() ,
, ![]() and
and ![]() :
:
First, construct an orthonormal basis for the space:
The component in the space is given by ![]() :
:
The difference ![]() is perpendicular to any vector in the span of the
is perpendicular to any vector in the span of the ![]() :
:
Least Squares and Curve Fitting (3)
If the linear system ![]() has no solution, the best approximate solution is the least-squares solution. That is the solution to
has no solution, the best approximate solution is the least-squares solution. That is the solution to ![]() , where
, where ![]() is the orthogonal projection of
is the orthogonal projection of ![]() onto the column space of
onto the column space of ![]() . Consider the following
. Consider the following ![]() and
and ![]() :
:
The linear system is inconsistent:
Find an orthonormal basis for the space spanned by the columns of ![]() :
:
Compute the orthogonal projection![]() of
of ![]() onto the spaced spanned by the
onto the spaced spanned by the ![]() :
:
Visualize ![]() , its projections
, its projections ![]() onto the
onto the ![]() and
and ![]() :
:
Confirm the result using LeastSquares:
Orthogonalize can be used to find a best-fit curve to data. Consider the following data:
Extract the ![]() and
and ![]() coordinates from the data:
coordinates from the data:
Let ![]() have the columns
have the columns ![]() and
and ![]() , so that minimizing
, so that minimizing ![]() will be fitting to a line
will be fitting to a line ![]() :
:
Get the coefficients ![]() and
and ![]() for a linear least‐squares fit:
for a linear least‐squares fit:
Verify the coefficients using Fit:
Plot the best-fit curve along with the data:
Find the best-fit parabola to the following data:
Extract the ![]() and
and ![]() coordinates from the data:
coordinates from the data:
Let ![]() have the columns
have the columns ![]() ,
, ![]() and
and ![]() , so that minimizing
, so that minimizing ![]() will be fitting to
will be fitting to ![]() :
:
Construct orthonormal vectors ![]() that have the same column space as
that have the same column space as ![]() :
:
Get the coefficients ![]() ,
, ![]() and
and ![]() for a least‐squares fit:
for a least‐squares fit:
Verify the coefficients using Fit:
Matrix Decompositions (2)
Find an orthonormal basis for the column space of the following matrix ![]() , and then use that basis to find a QR factorization of
, and then use that basis to find a QR factorization of ![]() :
:
Apply Gram–Schmidt to the columns of ![]() , then define
, then define ![]() as the matrix whose columns are those vectors:
as the matrix whose columns are those vectors:
Compare with the result given by QRDecomposition; the ![]() matrices are the same:
matrices are the same:
The ![]() matrices differ by a transposition because QRDecomposition gives the row-orthonormal result:
matrices differ by a transposition because QRDecomposition gives the row-orthonormal result:
For a Hermitian matrix (more generally, any normal matrix), the eigenvectors are orthogonal, and it is conventional to define the projection matrices ![]() , where
, where ![]() is a normalized eigenvector. Show that the action of the projection matrices on a general vector is the same as projecting the vector onto the eigenspace for the following matrix
is a normalized eigenvector. Show that the action of the projection matrices on a general vector is the same as projecting the vector onto the eigenspace for the following matrix ![]() :
:
Find the eigenvalues and eigenvectors:
![]() and
and ![]() are both orthogonal to
are both orthogonal to ![]() since they come from different eigenspaces:
since they come from different eigenspaces:
They need not and are not orthogonal to each other, since they have the same eigenvalue:
Use Orthogonalize to create an orthonormal basis out of the ![]() :
:
Compute the projection matrices:
Confirm that multiplying a general vector by ![]() equals the projection of the vector onto
equals the projection of the vector onto ![]() :
:
Since the ![]() form an orthonormal basis, the sum of the
form an orthonormal basis, the sum of the ![]() must be the identity matrix:
must be the identity matrix:
General Inner Products and Function Spaces (4)
A positive-definite, real symmetric matrix or metric ![]() defines an inner product by
defines an inner product by ![]() :
:
Being positive-definite means that the associated quadratic form ![]() is positive for
is positive for ![]() :
:
Note that Dot itself is the inner product associated with the identity matrix:
Orthogonalize the standard basis of ![]() to find an orthonormal basis:
to find an orthonormal basis:
Confirm that this basis is orthonormal with respect to the inner product ![]() :
:
Fourier series are projections onto an orthonormal basis in the inner product space ![]() . Define the standard inner product on square-integrable functions:
. Define the standard inner product on square-integrable functions:
Orthogonalize functions of the form ![]() in this inner product:
in this inner product:
![]() equals the symmetric Fourier coefficient corresponding to FourierParameters{0,1}:
equals the symmetric Fourier coefficient corresponding to FourierParameters{0,1}:
Confirm using FourierCoefficient:
The Fourier series is the projection of ![]() onto the space spanned by the
onto the space spanned by the ![]() :
:
Confirm the result using FourierSeries:
LegendreP defines a family of orthogonal polynomials with respect to the inner product ![]() . Orthogonalize the polynomials
. Orthogonalize the polynomials ![]() for
for ![]() from zero through four to compute scalar multiples of the first five Legendre polynomials:
from zero through four to compute scalar multiples of the first five Legendre polynomials:
Compare to the conventional Legendre polynomials:
For each ![]() ,
, ![]() and
and ![]() differ by a factor of
differ by a factor of ![]() :
:
HermiteH defines a family of orthogonal polynomials with respect to the inner product ![]() . Apply the unnormalized Gram–Schmidt process to the polynomials
. Apply the unnormalized Gram–Schmidt process to the polynomials ![]() for
for ![]() from zero through four to compute scalar multiples of the first five Hermite polynomials:
from zero through four to compute scalar multiples of the first five Hermite polynomials:
Properties & Relations (9)
For linearly independent vectors, the result is an orthonormal set:
This extends to any inner product:
For ![]() linearly independent
linearly independent ![]() -vectors, the result is a unitary matrix:
-vectors, the result is a unitary matrix:
If the vectors are real-valued, the matrix is additionally orthogonal:
If input vectors are not linearly independent, the result is padded with zero vectors to a matching length:
If ![]() is the result of Orthogonalize[vecs],
is the result of Orthogonalize[vecs], ![]() is a diagonal matrix:
is a diagonal matrix:
It only has ones and zeroes on the diagonal:
Zeroes on the diagonal correspond to zero vectors in the result:
In ![]() dimensions, there can be at most
dimensions, there can be at most ![]() elements in the orthonormal basis:
elements in the orthonormal basis:
Most sets of random ![]() -dimensional vectors are spanned by exactly
-dimensional vectors are spanned by exactly ![]() basis vectors:
basis vectors:
With the default method, the first element of the basis is always a multiple of the first vector:
Orthogonalize can be implemented by repeated application of Projection and Normalize:
Orthogonalize[m] is related to QRDecomposition[Transpose[m]]:
See Also
OrthogonalMatrixQ UnitaryMatrixQ Projection Normalize Dot Inner QRDecomposition LinearSolve
Function Repository: FullQRDecomposition
Tech Notes
Related Guides
History
Text
Wolfram Research (2007), Orthogonalize, Wolfram Language function, https://reference.wolfram.com/language/ref/Orthogonalize.html.
CMS
Wolfram Language. 2007. "Orthogonalize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Orthogonalize.html.
APA
Wolfram Language. (2007). Orthogonalize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Orthogonalize.html
BibTeX
@misc{reference.wolfram_2025_orthogonalize, author="Wolfram Research", title="{Orthogonalize}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Orthogonalize.html}", note=[Accessed: 03-November-2025]}
BibLaTeX
@online{reference.wolfram_2025_orthogonalize, organization={Wolfram Research}, title={Orthogonalize}, year={2007}, url={https://reference.wolfram.com/language/ref/Orthogonalize.html}, note=[Accessed: 03-November-2025]}