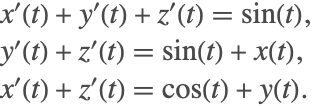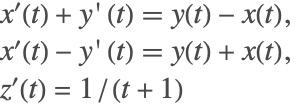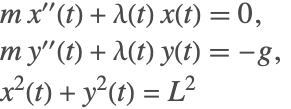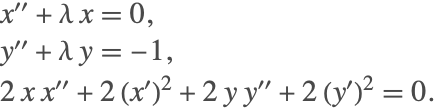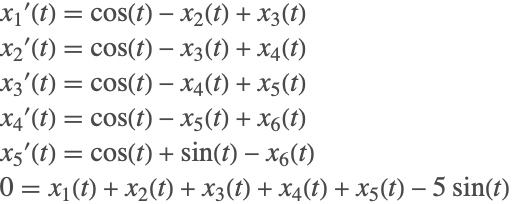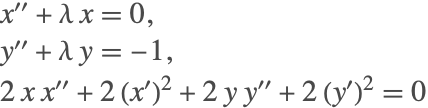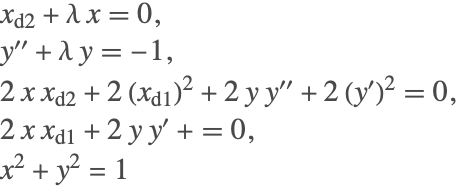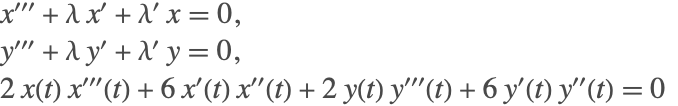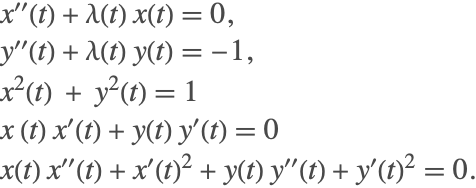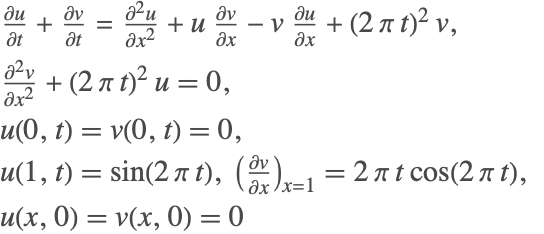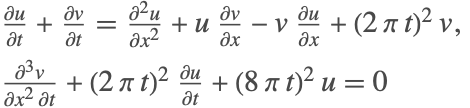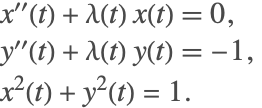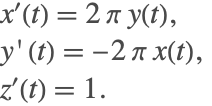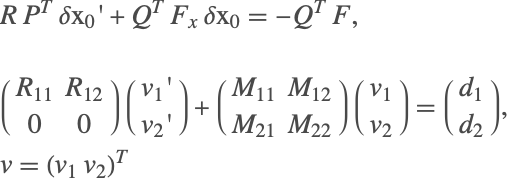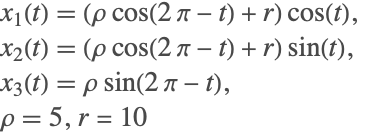Numerical Solution of Differential-Algebraic Equations
Introduction
In general, a system of ordinary differential equations (ODEs) can be expressed in the normal form,
The derivatives of the dependent variables 
are expressed explicitly in terms of the independent transient variable 
and the dependent variables 
. As long as the function 
has sufficient continuity, a unique solution can always be found for an initial value problem where the values of the dependent variables are given at a specific value of the independent variable.
With differential-algebraic equations (DAEs), the derivatives are not, in general, expressed explicitly. In fact, derivatives of some of the dependent variables typically do not appear in the equations. For example, the following equation
does not explicitly contain any derivatives of 
. Such variables are ofter referred to as algebraic variables.
The general form of a system of DAEs is
Solving systems of DAE often involves many steps. The flow chart shown below indicates the general process associated with solving DAEs in NDSolve.
Flow chart of steps involved in solving DAE systems in NDSolve.
Generally, a system of DAEs can be converted to a system of ODEs by differentiating it with respect to the independent variable 
. The index of a DAE is the number of times need to differentiate the DAEs to get a system of ODEs.
The DAE solver methods built into NDSolve work with index-1 systems, so for higher-index systems an index reduction may be necessary to get a solution. NDSolve can be instructed to perform that index reduction. When a system is found to have an index greater than 1, NDSolve generates a message and number of steps need to be taken in order to solve the DAE.
As a first step for high-index DAEs, the index of the system needs to be reduced. The process of differentiating to reduce the index, referred to as index reduction, can be done in NDSolve with a symbolic process.
The process of index reduction leads to a new equivalent system. In one approach, this new system is restructured by substituting new (dummy) variables in place of the differentiated variables. This leads to an expanded system that then can be uniquely solved. Another approach for restructuring the system involves differentiating the original system 
number of times until the differentials for all the variables are accounted for. The preceding 
differentiated systems are treated as invariants.
In order to solve the new index-reduced system, a consistent set of initial conditions must be found. A system of ODEs in normal form, 
, can always be initialized by giving values for 
at the starting time. However, for DAEs it may be difficult to find initial conditions that satisfy the residual equation 
; this amounts to solving a nonlinear algebraic system where only some variables may be independently specified. This will be discussed in further detail in a a later section. Furthermore, the initialization needs to be consistent. This means that the derivatives of the residual equations 
also need to be satisfied. Commonly, higher-index systems are harder to initialize. In this case NDSolve cannot, in general, see how the components of 
interact and is thus not able do an automatic index reduction. NDSolve, however, has a number of different methods, accessible via options, to perform index reduction and find a consistent initialization of DAEs.
The remainder of this document is structured in the following manner: First some terminology around indices of DAEs is introduced. Following that, the next section treats solving of index-1 DAEs. Next, methods for index reduction of higher-order index DAEs are presented. Consistent initialization of DAEs is treated subsequently. In addition to the examples in the sections mentioned so far, an entire last section with additional examples is given.
This loads packages that will be used in the examples.
Index of a DAE
For a general DAE system 
, the index of the system refers to the minimum number of differentiations of part or all the equations in the system that would be required to solve for 
uniquely in terms of 
and 
. Note that there are many slightly different concepts of index in the literature; for the purpose of this document the preceding concept will be used.
Consider the following DAE
In order to get a differential equation for 
, the first equation must be differentiated once. This leads to the new system
The differentiated system now contains 
, which must be accounted for. To get an equation for 
, the second equation must now be differentiated three times. This leads to
Since, part of the system had to be differentiated three times to get a derivative equation for 
, the index of the DAE is 3. The final differentiated system is said to be an index-0 system. To see ODEs that are obtained by the differentiations, you can perform appropriate substitutions, in this case subtracting the second equation from the first. The resulting equation can be written as
Similarly, the index-1 system can be found by differentiating the second equation twice, resulting in the following system
It is typical to reduce the index of the system to 1, since the underlying integration routines can handle them efficiently.
The index of a DAE may not always be obvious. Consider a system that may exhibit index-1 or index-2 behavior, depending on what the initial conditions are.
A system of DAEs with three equations, but only one differential term.
For this DAE, the initial conditions are not free; the second equation requires that 
be either 0 or 1.
If 
, then the two remaining equations make an index-1 system, since differentiation of the third equation gives a system of two ODEs
While the initial condition for 
, the initial condition for 
can be varied.
Solve the system of DAEs starting with a specified initial condition for
and with
.
| Out[7]= |  |
| Out[8]= |  |
On the other hand, if 
, then the two remaining equations make an index-2 system. Differentiating the third equation gives 
, and substituting into the first equation gives 
, which needs to be differentiated to get an ODE
There are also no additional degrees of freedom in the initial conditions, since 
and 
.
Solve the system of DAEs starting with
.
| Out[9]= |  |
| Out[10]= |  |
Both the number of initial conditions needed and the index of a DAE may influence the actual solution being found.
Treatment of Differential Equations.
In order to solve a differential equation, NDSolve converts the user-specified system into one of three forms. This step is quite important because depending on how the system is constructed, different integration methods are chosen.
You may specify in which form to represent the equations by using the option Method->{"EquationSimplification"->simplification}. The following simplification methods can be specified for the 
option.
| Automatic | try to solve the system symbolically in the form  ; if a solution cannot be long or takes too long, try simplifying using the "MassMatrix" or  methods; this is the default |
| "Solve" | solve the system symbolically in the form  if possible |
| "MassMatrix" | reduce the system to the form  if possible |
| "Residual" | subtract right-hand sides of equations from left-hand sides to form a residual function  |
Options for EquationSimplification.
Consider the system
By default, an attempt is made to solve for the derivatives 
explicitly in terms of the independent and dependent variables, 
and 
. For efficiency purposes, NDSolve first attempts to try to find the explicit system by using LinearSolve. If that fails, however, then the system is solved symbolically using Solve.
NDSolve automatically tries to put the system in an explicit form.
| Out[12]= |  |
Using the 
method is the same as the default when a symbolic solution is found.
Generate a system of the form
using the option
.
| Out[14]= |  |
Out[15]//MatrixForm= |
| |  |
Generate a system of the form
using the option
.
| Out[17]= |  |
When the system is put in a residual form, the derivatives are represented by a new set of variables that are generated to be unique symbols. You can get the correspondence between these working variables and the specified variables using the 
and 
properties of NDSolveStateData.
Show correspondence between working and specified variables.
| Out[18]= |  |
The process of generating an explicit system of ODEs may sometimes become expensive due to the symbolic treatment of the system. For this reason, there is a time constraint of one second put on obtaining the equations. If that time is exceeded, then NDSolve generates a message and attempts to solve the system as a DAE.
Define variables and equations for a nonlinear system.
Solve using the default equation simplification strategy.
| Out[22]= |  |
As indicated by the message, NDSolve did not solve explicitly for the derivatives because Solve had exceeded the default time constraint of one second. The amount of time that NDSolve spends on obtaining an explicit expression can be controlled using the option 
.
Use the suboption option
to control the amount of time in seconds
NDSolve spends on obtaining an explicit expression.
| Out[23]= |  |
In the preceding example, due to the square terms in the first equation, four possible solutions are encountered. When solving as a DAE, the numerical solution will only follow one of these solution branches, depending on how it is initialized.
DAE Solution Methods
There are a variety of solution methods built into NDSolve for solving DAEs.
Two methods work with the general residual form of index-1 DAEs, 
.
IDA—(Implicit Differential-Algebraic solver from the SUNDIALS package) based on backward differentiation formulas (BDF)
StateSpace—implicitly solves 
for derivatives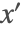 
to use an underlying ODE solver
If the system has index higher than 1, both of these solvers typically fail. To accurately solve such systems, index reduction is needed. Note that index-1 systems can be reduced to ODEs, but it is often more efficient to use one of the solvers above.
NDSolve also has some solvers that work with DAEs that can be reduced to special forms.
MassMatrix—for DAEs of the form 
Projection—for ODEs 
with invariants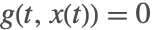 
The following subsections describe some aspects of using these methods for DAEs.
ODEs with invariants
It is common to encounter DAEs of the form
where 
is an invariant that is consistent with the differential equations.
When a system of DAEs is converted to ODEs via index reduction, the equations that were differentiated to get the ODE form are consistent with the ODEs, and it is typically important to make sure those equations are well satisfied as the solution is integrated.
Such systems have more equations than unknowns and they are overdetermined unless the constraints are consistent with the ODEs. NDSolve does not handle such DAEs directly because it expects a system with the same number of equations and dependent variables. In order to solve such systems, the "Projection" method built into NDSolve handles the invariants by projecting the computed solution onto 
after each time step. This ensures that the algebraic equations are satisfied as the solution evolves.
An example of such a constrained system is a nonlinear oscillator modeling the motion of a pendulum.
This defines the equation, invariant constraint, and starting condition for a simulation of the motion of a pendulum.
Note that the differential equation is effectively the derivative of the invariant, so one way to solve the equation is to use the invariant.
NDSolve does not solve this system directly, as indicated by the message.
Using the
"Projection" time integration method gets a solution that satisfies the invariant at the time steps.
| Out[28]= |  |
| Out[29]= |  |
| Out[29]= |  |
| Out[7]= |  |
Plot the invariant at the time steps; it is satisfied nearly to machine precision.
| Out[29]= |  |
Solving Systems with a Mass Matrix
When the derivatives appear linearly, a differential system can be written in a form
where 
is a matrix often referred to as a mass matrix. Sometimes 
is also referred to as a damping matrix. If the matrix is nonsingular, then it can be inverted and the system can be solved as an ODE. However, in the presence of a singular matrix, the system can be solved as a DAE. In either case, it may be advantageous to take advantage of the special form.
The system describing the motion of a particle on a cylinder
can be expressed in mass matrix form with
Define system variables, equations, and initial conditions.
Solve the system in the form
using the option
.
| Out[34]= |  |
Index Reduction for DAEs
The built-in solvers for DAEs in NDSolve currently handle index-1 systems of DAEs fully automatically. For higher-index systems, an index reduction is necessary to get to a solution. This index reduction can be performed by giving appropriate options to NDSolve.
NDSolve uses symbolic techniques to do index reduction. This means that if your DAE system is expressed in the form 
, where NDSolve cannot see how the components of 
interact and compute symbolic derivatives, the index reduction cannot be done, and for this reason NDSolve does not do index reduction, by default.
For an example, consider the classic DAE describing the motion of a pendulum:
where there is a mass 
at the point 
constrained by a string of length 
. 
is a Lagrange multiplier that is effectively the tension in the string. For simplicity in the description of index reduction, take 
. The figure shows the schematic of the pendulum system.
Sketch of the forces acting on a pendulum.
If the index of the system is not obvious from the equations, one thing to do is to just try it in NDSolve, and if the solver is not able to solve it, in many cases it is able to generate a message indicating what the index appears to be for the initial conditions specified.
Define equations and a complete set of initial values for the constrained pendulum system.
Try to solve the constrained pendulum system.
| Out[42]= |  |
The message indicates that the index is 3, indicating that index reduction is necessary to solve the system. Note that a complete consistent initialization is used here to avoid possible issues with initialization. This aspect of the solution procedure is treated in "Consistent Initialization of DAEs" with more detail.
The option setting Method->{"IndexReduction"->{irmeth, iropts}}, is used to specify that NDSolve uses index reduction method irmeth with general index reduction options iropts.
| None | no index reduction (default) |
| Automatic | choose the method automatically |
| "Pantelides" | graph-based Pantelides algorithm |
| "StructuralMatrix" | structural matrix-based algorithm |
Index reduction methods.
The following options can be given for all index reduction methods.
| "ConstraintMethod" | Automatic | how to handle constraints from specified system |
| "IndexGoal" | Automatic | index to reduce to (1 or 0) |
Options for index reduction.
Solve using automatically chosen methods of index reduction.
| Out[43]= |  |
| Out[44]= |  |
Index reduction is done by differentiating equations in the DAE system. Suppose that an equation eqn is differentiated during the process of index reduction so that 
is included in the system in place of eqn. Once the differentiation has been done, the differentiated equations comprise a fully determined system and can be solved on their own. However, it is typically important to incorporate the original equations in the system as constraints. How this is done is controlled by the 
index reduction option.
| None | do not keep the original equations as constraints and just solve with the differentiation equations |
| "DummyDerivatives" | use the method of Mattson and Soderlind [MS93] to replace some derivatives with algebraic variables (dummy derivatives) |
| "Projection" | reduce the index to 0 to get an ODE and use the  time integration method with the original equations that were differentiated as invariants |
Constraint methods.
Use index reduction and solve with the differentiated equations
Compare how well the constraint
is satisfied for the two solutions.
| Out[46]= |  |
In the numerical solution with just the differentiated equations, the length of the pendulum is drifting away from 1. Incorporating the original equations into the solution as constraints is an important aspect of index reduction.
The next two sections will describe index reduction algorithms, followed by an explanation of constraint methods that can be used in NDSolve.
Index Reduction Algorithms
NDSolve has two algorithms for doing index reduction, the Pantelides and the structural matrix methods. Both of these methods use the symbolic form of the equations to determine which equations to differentiate and then use symbolic differentiation to get the differentiated system.
Both methods make use of the concept of structural incidence in the equations; in particular if variable 
appears explicitly in equation 
, then 
is termed incident in 
. The structural incidence matrix is the matrix with elements 
if 
is incident in 
and otherwise 
. A DAE system has structural index 1 if the structural incidence matrix can be reordered so that there are 1s along the diagonal. The existence of such a reordering means that there is a matching between equations and variables such that there is one equation for every variable.
The Pantelides algorithm works with a graph based on the incidence that can be very efficient even for extremely large systems.
Note that the structural index may be smaller than the actual index of the system. In the real system, terms that are structurally present may vanish along some solutions or the Jacobian matrix may be singular. The structural matrix method tries to take into account the possibility of singularities in the Jacobian and will do a better job of index reduction for some systems, but at the cost of greater computational expense.
The next section introduces a command for getting the structural incidence matrix that is useful for the descriptions of the Pantelides and structural matrix algorithms that follow in the subsequent sections.
Structural Incidence
| NDSolve`StructuralIncidenceArray[eqns,vars] | return a SparseArray that has the pattern of the structural incidence matrix for the variables vars in the equations eqns |
Getting the structural incidence.
Get the structural incidence matrix for the system
,
for the variables
,
.
| Out[47]= |  |
Out[48]//MatrixForm= |
| |  |
Note that the SparseArray contains just the nonzero pattern that uses less memory and indicates it represents the pattern of incidence. It can be converted to a SparseArray with 1s using ArrayRules.
Define a command to convert pattern arrays to 1s and 0s.
| Out[50]= |  |
| Out[51]= |  |
Out[52]//MatrixForm= |
| |  |
The system has structural index 1, since no reordering is needed to avoid zeros along the diagonal.
If the structural incidence with respect to the derivative variables can be arranged to avoid zeros on the diagonal, then the system is index 0.
Get the structural incidence matrix for the system
,
for the variables
,
.
Out[53]//MatrixForm= |
| |  |
There is no reordering that will avoid zeros on the diagonal. However, if the second equation is differentiated it is possible.
Get the structural incidence matrix for the system
,
with the second equation differentiated for the variables
,
.
Out[54]//MatrixForm= |
| |  |
So the differentiated system has structural index 0, verifying that the original system was index 1.
Consider the constrained pendulum (2) as another example.
Get the structural incidence matrix for the constrained pendulum system with respect to the highest-order derivatives that appear.
Out[55]//MatrixForm= |
| |  |
The matrix cannot be reordered to avoid zeros on the diagonal, so the index is greater than 1.
Note that the function 
just does a literal matching on the FullForm of the expression to check for the incidence. It does not do any checking to see if your equations or variables are properly formed.
This tests the literal presence of the symbols
x and
y in each of the equations.
Out[56]//MatrixForm= |
| |  |
This is a full matrix because the FullForm of 
is Derivative[1][x][t] that contains x.
Pantelides Method
The method proposed by Pantelides [P88] is a graph theoretical method that was originally proposed for finding consistent initialization of DAEs. It works with a bipartite graph of dependent variables and equations, and when the algorithm can find a traversal of the graph, then the system has been reduced to index at most 1. A traversal in this sense effectively means an ordering of variables and equations so that the graph's incidence matrix has no zeros on the diagonal.
When the bipartite graph does not have a complete traversal, the algorithm effectively augments the path by differentiating equations, introducing new variables (derivatives of previous variables) in the process. Unless the original system is structurally singular, the algorithm will terminate with a traversal. Generally, the algorithm does only the differentiations needed to get the traversal, but since it is a greedy algorithm, it is not always the minimal number.
It is beyond the scope of this documentation to describe the algorithm in detail. The implementation built into Mathematica follows the algorithm outlined in [P88] fairly closely. It uses Graph to efficiently implement the graph computations and symbolically differentiates the equations with D when differentiation is called for.
When there is a traversal of the system, it is then possible to find an ordering for the variables and equations such that the incidence matrix is in block lower triangular (BLT) form. The BLT form is used in setting up the dummy derivative method for maintaining constraints and also in the 
time integration method. A description of the BLT ordering is included in "State Space Method for DAEs".
To begin index reduction on the constrained pendulum system (2), consider the variables 
. Generally, start with the highest-order derivative that appears in the equations. As a reminder, the pendulum equations are
and the graph incidence matrix with respect to the highest order derivative is
The incidence matrix is constructed by checking the presence of a variable in an equation. If the variable exists in the equation, a weight of 1 is given; if not then 0 is specified. So, checking for the variables 
in the first equation gives 
(as seen in the first row of the incidence matrix).
From the first incidence matrix, it is found that there is no traversal. The last equation is differentiated twice
The incidence matrix is now
This can be reordered so that there is no zero on the diagonal by swapping the first and last equations, resulting in the incidence matrix
The resulting system has index 1 since 
still appears as an algebraic variable and does not contain a derivative in the differentiated system. Differentiating the system one more time will provide a differential system for 
. Therefore, the index of the original system is indeed 3.
As a first approach, the system with the twice-differentiated equation can be solved directly.
Solve the system with the twice-differentiated equation.
| Out[57]= |  |
Plot quantities that should be invariant, based on the originally specified equations.
| Out[58]= |  |
The original pendulum length constraint is not being satisfied well; in fact, it stretches! The constraints are not satisfied well because the new system does not identically represent the original system. This can be seen by the fact that the new system does not contain the original constraint of 
, but rather its differentiated equations.
To model the original dynamics of the system with the new system, additional equations must be satisfied. However, including additional equations leads to more equations than unknowns. To address this issue, the method of dummy derivatives is used, so that the index reduced system becomes balanced.
The Pantelides algorithm is efficient because it can use graph algorithms with well-controlled complexity even for very large problems. However, since it is based solely on incidence, there can be issues with systems that lead to Jacobians that are singular. The structural matrix method may be able to resolve such cases, but may have larger computational complexity for large systems.
Structural Matrix Method
The structural matrix algorithm is an alternative to the Pantelides algorithm. The structural matrix method follows from the work of Unger [UKM95] and Chowdhary et. al. [CKL04]. The graph-based algorithms such as the Pantelides algorithm rely on traversals to perform index reduction. However, they do not account for the fact that sometimes there may be variable cancellations in a particular system. This leads to the algorithm underestimating the index of the system. If a DAE has not been correctly reduced to an index-0 or index-1 system, then the numerical integration may fail or may produce an incorrect result.
As an example of variable cancellation that is not taken into account by Pantelides's method consider the following DAE
.
To perform index reduction, as a first step the second equation is differentiated once, giving:
.
The Pantelides algorithm stops after the first differentiation because it finds derivatives for the variables 
and finds a traversal. Since all the derivatives are found from the first differentiation, the Pantelides algorithm estimates the index of the system to be 0. An index-0 system is equivalent to a system of ODEs. The Jacobian of the derivatives for the differentiated system is found to be
and is clearly singular. By simple substitutions, it is possible to see that the differentiated system is equivalent to
.
This implies that in order to get a system of ODEs, a second differentiation must be done for the second equation. This results in the final system
.
The above system has a nonsingular Jacobian for the derivatives. The above system is now correctly index 0 and a system of ODEs can be formed from it. Since two differentiations were required, the actual index of the system is actually 2 (instead of 1).
Unlike the Pantelides algorithm, the structural matrix method accounts for all cancellations associated with the linear terms. The steps of the method are demonstrated using the pendulum example (2) described as a first-order system
As a first step, two matrices 
and 
are constructed. The matrices are incidence matrices associated with the derivatives 
and the variables 
, respectively. For the above system, the matrix 
is given as
The matrix above contains a * as some of its entries. The * is used as a placeholder, indicating that the variables in that equation (row) are present in the equation in a nonlinear fashion. Notice that for the second equation, the terms 
and 
appear as products. Therefore, the first and last columns in the second row are marked with a *.
Once the matrices are constructed, the objective is to try and convert the system of DAEs into a system of ODEs. In order to do that, the rank of the matrix 
must be full. To achieve this, equations that need to be differentiated are first identified. In this case, it is the last equation. After differentiation, the structural matrices are
The last column of the matrix 
has changed due to the differentiations. To see this more clearly, consider the last equation in (3). Differentiating the equation gives 
. Notice now that the terms 
are present in the equation and appear in a nonlinear manner. Therefore the incidence row associated with the derivatives is 
and the incidence row associated with the variables is 
.
The next step involves matrix factorization in the form of Gaussian elimination for the matrix 
. The elements in the last row of 
can be eliminated by making use of rows 1 and 3. This elimination also effects the rows of the matrix 
. Multiplying the first row of 
with * and subtracting it with the last row leads to
Multiplying the third row with * and subtracting it from the last row gives
The matrix 
is still rank deficient and therefore the above steps must be repeated. A second iteration leads to the system
A third iteration leads to the system
The matrix 
is now a full-rank matrix. Therefore the iterations are stopped. Since three iterations were needed to get a full-rank matrix for 
, the index of the system is 3. Note that unlike the Pantelides method, the structural matrix algorithm explicitly operates on the incidence matrices.
The next examples demonstrate the advantage and differences of the structured matrix method over the Pantelides algorithm. Consider the linear system
.
Set up the equations and initial conditions.
Try solving the system using the Pantelides algorithm.
| Out[61]= |  |
This fails because there is a singular Jacobian matrix. Very commonly the messages NDSolve::nderr or NDSolve::ndcf are issued by the solver when the DAE's index is greater than 1.
Solve the system using the structural matrix method for index reduction.
| Out[62]= |  |
The exact solutions are 
and 
. Comparing the exact and numerical results, it is found that the computed solution is quite accurate.
| Out[63]= |  |
Next, consider the effect of under- or overestimating the index of a system. Consider the linear system
.
Set up the equations, initial conditions, and variables.
The exact solution for all the variables is 
. This is an index-4 system. The Pantelides algorithm estimates the index to be 2.
Attempt to solve the system using the Pantelides algorithm for index reduction.
The solver encounters a convergence failure because the Jacobian is singular.
Solve the system using the structural matrix algorithm for index reduction.
| Out[72]= |  |
There are certain tests that NDSolve performs to determine which index reduction method to use. For this case, using the option 
, NDSolve picks the structural matrix algorithm.
Solve the system by setting the
.
| Out[73]= |  |
If the system is forced to be treated as index 0, integration can be performed. However, in the absence of incorrect estimation of the index, the results can be wildly off because the solution is being computed for a completely different manifold.
Solve the system as an index-0 system using the Pantelides algorithm.
| Out[74]= |  |
Since the exact solution is known for this problem, it is desirable to see the difference between the numerical solution and the exact result.
| Out[75]= |  |
Due to the underestimation of the index of the system, the necessary differentiations are not carried out, leading to the solution's being approximated on an incorrect manifold. The structural matrix method, on the other hand, is able to correctly identify the index of the system.
Plot the result of the system as obtained using
.
| Out[76]= |  |
Solve the system as an index-0 system using the structural matrix method.
| Out[78]= |  |
The structural matrix method does handle such systems much better. It is, however, important to note that there is a price to be paid for the rigor of accounting for cancellations. The structural matrix method relies on generating, maintaining, and operating on matrices, which has a significant computational overhead compared to the Pantelides algorithm. The algorithm is therefore only suited for small- to medium-scale problems.
Constraint Methods
Dummy Derivatives
The purpose of the dummy derivative method is to introduce algebraic variables so that the combined system of original equations and equations that have been differentiated for index reduction is not overdetermined.
Consider the pendulum system (2) again.
This solves the system using the index reduction with dummy derivatives built into
NDSolve.
| Out[79]= |  |
Note that for this example the 
was included for emphasis and is not needed, since trying to use dummy derivatives is the default.
Plot quantities that should be invariant based on the originally specified equations.
| Out[80]= |  |
Now the constraints are very well satisfied.
The main idea behind the dummy derivative method of Mattson and Soderlind [MS93] is to introduce new variables that represent derivatives, thus making it possible to reintroduce constraint equations without getting an overdetermined system.
Recall the index-reduced equations for the system (2) were
with the two constraints from the third equation and its first derivative,
Let 
and 
be algebraic variables that replace 
and 
respectively. Then, with the constraints included, the entire system in these variables is given by
and the incidence matrix with variables 
is
that can be reordered to have a nonzero diagonal.
Reorder the incidence matrix.
Out[83]//MatrixForm= |
| |  |
In general, the algorithm can be applied to any index-reduced DAE; however, while integrating the system, the solver may encounter singularities.
Try to integrate the system with manually introduced dummy derivatives replacing
and
. (Using dummy derivatives is the default so no option setting is needed.)
| Out[84]= |  |
The above system cannot complete integration because the system becomes singular when 
.
This plots the solution as far as it was computed.
| Out[85]= |  |
From the plot it can be seen that NDSolve is getting stuck when 
is becoming 0. When 
is 0, several terms drop out, the incidence matrix becomes singular, and a nonzero diagonal can no longer be found, so the dummy derivative system effectively has index 
along solutions that go through 
.
Consider an alternative dummy derivative replacement, i.e. 
and 
to replace 
and 
. Unfortunately, the system with this replacement becomes singular at 
.
The remedy is to use dynamic state selection such that 
and 
replace 
and 
when 
is away from 0 and switch dynamically to the system using 
and 
to replace 
and 
when ![TemplateBox[{x}, Abs]](Files/NDSolveDAE.en/Image_208.png "TemplateBox[{x}, Abs]")
becomes too small. NDSolve automatically uses WhenEvent with state replacement rules to handle dynamic state selection with dummy derivatives if necessary. The exact details of the dynamic state selection are beyond the scope of this tutorial. A detailed explanation can be found in Mattson and Soderlind [MS93].
Projection
The alternative to using dummy derivatives is to reduce the index to 0 so there is a system of ODEs and use projection to ensure that the original constraints are satisfied.
For the pendulum system (2), the index of the system is 3. This means that in order to get an ordinary differential equation for all the variables, the first and second equations must be differentiated once while the third equation must be differentiated three times. This results in
that can be solved for the derivatives 
, 
, and 
. (NDSolve will also reduce the system to first order automatically.)
In order to correctly represent the dynamics of the system, the first 
differentiated equation must also be taken into account. These equations are
The above equations are treated as invariant equations that must be satisfied at each time step. Since the ODE system was derived from differentiating these equations, the constraints are guaranteed to be consistent with the ODEs, so the system can be solved using the "Projection" time integration method with the constraints as invariants.
| Out[86]= |  |
This can be done automatically the built-in index reduction in NDSolve directly.
This solves the system using the index reduction with projection built into
NDSolve.
With this method, the original constraints are typically satisfied up to the local tolerances for NDSolve specified by the PrecisionGoal and AccuracyGoal options.
The system has additional invariants that should also be satisfied. One of these is the conservation of energy that can be expressed by 
. Because the projection method only projects at the ends of the time steps, this is the most appropriate place to do the comparison.
This gets the energy for a solution at the time steps and plots the energy for the dummy derivative and projection solutions.
| Out[90]= |  |
Consistent Initialization of DAEs
A system of differential algebraic equations (DAEs) can be represented in the most general form as
,
which may include differential equations and algebraic constraints. In order to obtain a solution for 
, a set of consistent initial conditions for 
and 
is needed to start the integration. A necessary condition for consistency is that the initial conditions satisfy 
However, this condition alone may not be sufficient, since differentiating the original equations produces new equations that also need to be satisfied by the initial conditions. The task therefore is to try and find initial conditions that satisfy all necessary consistency conditions. The problem of finding consistent initial conditions can be one of the most difficult parts of solving a DAE system.
Consider the following linear DAE problem:
.
The DAE has derivatives for 
. This would suggest that in order to uniquely solve this problem, initial conditions for 
need to be specified. However, you cannot specify any arbitrary initial conditions to the variables, since there is a unique set of consistent initial conditions. Differentiating the algebraic equation once leads to 
Substituting in the second equation gives the solution for 
. Differentiating 
and substituting into the first equation gives the solution for 
This shows that the solution for the DAE system is fixed, and therefore the initial conditions are also fixed, and the only consistent set of initial conditions for 
is 
It is important to note that the constraints on the initial conditions are not obvious, in general making the problem of finding consistent initial conditions quite challenging.
In some cases, you may just want to get a consistent initialization for a DAE problem and not compute the solution further. This can be done with NDSolve by specifying the endpoint of the time integration to be the same as the time where the initial condition is specified. Such a step is generally helpful when you need to examine just the starting conditions without having to perform the complete integration.
This computes initial conditions for a system of DAEs.
| Out[91]= |  |
| Out[92]= |  |
NDSolve provides several methods for DAE initialization. The method m can be specified using Method->{"DAEInitialization"->m}.
| Automatic | determine the method to use automatically |
| "Collocation" | use a collocation method; this algorithm can be used for initialization of high-index systems. |
| "QR" | use a QR decomposition-based algorithm for index-1 systems. |
| "BLT" | use a Block Lower Triangular ordering (BLT) approach for index-1 systems. |
Methods for DAE initialization.
The collocation method is designed to handle the DAE system as a residual black box and tries to achieve the objective of satisfying the residual over a small interval near the point of initialization. This feature allows the method to be used to handle initialization of high-index systems. However, since the algorithm does not analyze the DAE system, the structure of the system cannot be exploited for computational efficiency. This makes the algorithm slower than the other methods.
The QR and BLT methods are designed specifically to be used for index-1 and index-0 systems. The QR method relies on decomposing the Jacobian of the derivative to generate two decoupled subsystems such that the initial conditions for the variables and their derivatives are computed iteratively. This makes the method quite efficient and robust.
The BLT method relies on examining the structure of the DAE system and splits the original system into a number of smaller subsystems such that each of these subsystems can be solved efficiently. This method results in dealing with much smaller Jacobian matrices (compared to the entire system) and thus is computationally efficient for large systems.
The following sections give details about how NDSolve obtains consistent initial conditions for DAEs using different algorithms.
Collocation Method
The basic collocation algorithm makes use of expanding the dependent variables 
in terms of basis functions 
as
In order to obtain 
and 
, one tries to enforce the condition that 
is satisfied at 
collocation points, 
, in time. To achieve this, the implicit DAE is linearized as
where 
and 
denote the Jacobian of 
with respect to 
and 
, respectively:
,
.
Applying this linearization to 
collocation points in time, a system of linear equations is obtained for the coefficients 
, which is solved iteratively using Newton's method.
where 
is obtained using a line search method. If there are 
coefficients and 
collocation points, then you are dealing with an 
×
system of linear equations in (5).
For high-index systems that have not index reduced, NDSolve automatically tries to initialize the system using the collocation algorithm. Consider the pendulum system (2)
In order to start integration of the system, the initial conditions for 
must be known. For such systems, 
would represent some physical property and could be assigned reasonable values. However, the value of 
might not be easy to find. NDSolve can be used here to determine the appropriate values.
Obtain a consistent set of initial conditions for the pendulum DAE.
| Out[93]= |  |
| Out[94]= |  |
| Out[95]= |  |
Notice that only partial initial conditions were given and the algorithm correctly computes all the required initial conditions.
The default settings for the collocation method have been chosen to handle initialization for a wide variety of systems; however, in some cases it is necessary to change the settings to find a consistent Initialization. The following options may be used to tune the algorithm.
| | |
| "CollocationDirection" | Automatic | chooses the direction in which the collocation points are placed; possible options include  ,  ,  ,  |
| "CollocationPoints" | Automatic | number of collocation points to be used; using suboption  , more grid points are added while keeping the approximation order fixed |
| "CollocationRange" | Automatic | range over which the collocation points are distributed |
| "DefaultStartingValue" | Automatic | starting value used for unspecified components in the nonlinear iterations; option can be a one-element value  or a list of two numbers  , where  are the starting values for the variable and its derivative, respectively |
| "MaxIterations" | 100 | maximum number of iterations to be performed |
method options.
The next sections discuss these options in more detail and show in what circumstances they may help to find consistent initial conditions.
Collocation Direction
In order to perform the initialization, a set of collocation points is selected. The points can be placed on both sides, front, or back of the point of interest, using the options 
, 
, or 
respectively. The following table describes the effect of choosing one of these options.
| "Forward" | collocation performed over the range  |
| "Backward" | collocation performed over the range  |
| "Centered" | collocation performed over the range  |
suboptions.
The term 
above refers to the time at which the initial condition is computed. The term 
is the offset value. By default, NDSolve automatically chooses the direction in which the collocation is performed.
The collocation direction becomes important when dealing with discontinuities.
In this case, at time 
, 
is discontinuous.
NDSolve automatically sets the option for 
.
| Out[97]= |  |
| Out[98]= |  |
Applying a 
of 
will cause the solution to diverge.
| Out[99]= |  |
However, using the 
or 
direction, you can get correct convergence by avoiding the discontinuous derivative.
| Out[100]= |  |
In most cases, NDSolve automatically determines what the direction should be. However, if it is known that there could be discontinuities in a specific direction, then it can be avoided by using this setting. This in turn helps in reducing the computational time for NDSolve.
Collocation Points
The option 
refers to the number of collocation points, 
, as indicated in (5) that will be used in the series approximation (4). Depending on the collocation points, the order 
of the series in (4) is determined. The order of the series is 
. The collocation points are essentially the Chebyshev points distributed over the collocation range.
To illustrate the effect of 
, consider the following index-3 example.
The solution to the preceding DAE can be found analytically. The exact consistent initial conditions are as follows.
Out[104]//TableForm= |
| |  |
The default setting for finds the correct initialization:
Out[106]//TableForm= |
| |  |
A manual setting of collocation points is possible. Setting 
is equivalent to setting 
in (4). This means that the solution is approximated using constant and linear basis functions.
Do the initialization using constant and linear basis functions.
Out[108]//TableForm= |
| |  |
Even though the iterations converged, the results are not the correct consistent initial conditions. No message is issued because they satisfy the specified equations sufficiently well.
Test the initial conditions in the specified equations.
| Out[109]= |  |
Recall that for higher-index equations, consistent initial conditions should also work with the differentiated system.
Increasing the number of collocation points and thus allowing higher-order basis functions allows the algorithm to converge to the expected result.
Try solving the initialization problem with a range of collocation points.
Plotting the results as a function of the collocation points gives an indication of how the solution converges.
Red,
Green, and
Blue correspond to the variables
, respectively.
| Out[113]= |  |
Since the order of the approximation 
is determined by the collocation points 
, the resulting linearized system obtained in (4) will result in a square matrix, and the resulting system of linear equations can be solved efficiently using LinearSolve. However, it is quite possible that the resulting linear system may be ill conditioned or singular. Such systems are known to be sensitive and therefore can result in an unstable iteration. To resolve this issue, it is often desirable to solve an overdetermined system of equation using LeastSquares.
Using the suboption 
, the order of the series approximation is kept equal to 
in (4), but the value of 
in (5) is modified to 
, where 
is the extra collocation points. This, therefore, leads to an overdetermined system of equations in (5), which is solved using the least-squares method.
Initialize with an overdetermined system.
Out[115]//TableForm= |
| |  |
Collocation Range
For very high-index systems that have not undergone index reduction, the use of a much higher collocation order might be required, along with a specification of the range in which the collocation should take place. By default, the collocation range is computed based on the working precision and the number of basis functions used in expansion.
For an example an index-6 system for which an exact solution can be found will be used.
Define variables and equations for an index-6 linear system of DAEs.
Find the exact solution for this case can using
DSolve.
| Out[119]= |  |
Make a table of the initial conditions.
Out[120]//TableForm= |
| |  |
The default options for the initialization compute an incorrect result for some of the terms.
Out[122]//TableForm= |
| |  |
Typically it is necessary to use an approximation with an order higher than the index of the system. Since this is an index-6 system, you must rely on a higher-order approximation in (4). As mentioned in the previous subsection, this can be done using the option 
.
Initialize using sufficient points for an order-15 approximation.
Out[124]//TableForm= |
| |  |
A solution is found, but there are significant errors from the exact consistent initial conditions. The reason for the large error is that for this example the default points are too close together and so there is noticeable numerical round-off error.
Initialize using 15 collocation points spread over an extended collocation range of length 1 to avoid numerical round-off errors.
Out[126]//TableForm= |
| |  |
There is a close relationship between 
and 
. The collocation range is computed based on the number of collocation points so as to avoid excessive round-off errors and to accommodate higher-precision computations. Unless explicitly specified, the 
is computed as 
, where 
is the setting of the WorkingPrecision option and 
is the setting of the 
method option.
Specifying Initial Conditions
One of the main differences between ODEs and DAEs is that in order to integrate a system of ODEs, initial conditions for all the variables must be provided. On the other hand, for a DAE, some of these initial conditions may be fixed and must be computed directly from the system. To elaborate, consider the ODE
The initial conditions can be arbitrarily specified for the preceding system. Now consider a modification of the same system given as
This system is a DAE, but the dynamics are identical to the ODE system. The major difference now is that the initial conditions 
and 
are not fixed, but rather are determined by the algebraic equation.
The preceding example is simple enough that some determination can be made as to which variables are fixed and perhaps the initial conditions manually computed. However, as the system gets more complicated and large, you must rely on additional tools.
In certain cases, the initial conditions are completely determined by the system of equations. To illustrate this case, consider the following linear DAE system
.
Though the system contains two derivatives, the solution and the initial conditions are completely determined by the system. No additional information is needed.
Initialize the system with no initial conditions specified.
| Out[129]= |  |
Get the consistent initial conditions.
| Out[131]= |  |
| Out[132]= |  |
It is important to note that it is often not possible to know which conditions are fixed and which ones are free. One approach that could be taken to gain some insight into what the initial conditions ought to be and/or what order of magnitude the initial conditions are, the DAE equations can be directly put in NDSolve without initial conditions are manipulate the options for the method 
.
Consider the pendulum system (2) represented as a first-order system. In order to uniquely define the state of the system, only two initial conditions are needed.
First, consider the case when no initial conditions are given for this DAE system. By default, the starting guess is taken to be 1 for all variables that have not been specified. Since no index reduction is performed, NDSolve automatically chooses the collocation algorithm.
| Out[136]= |  |
Out[137]//TableForm= |
| |  |
It is observed that the algorithm was able to find one possible set of initial conditions out of the infinitely many possible sets. At this point, it is of course very sensitive to the starting guesses. It is also important to note that convergence of the iterations is not guaranteed.
The initial starting guess can be changed using the option 
for the collocation method. If an initial starting guess of 
is used, then a different set of valid solutions will be found.
Out[139]//TableForm= |
| |  |
As mentioned earlier, two initial conditions are sufficient to fix the state of the system. For the pendulum case, the value of 
and 
fixes the system.
Compute the initial condition for the pendulum system with two states fixed.
Out[141]//TableForm= |
| |  |
If the state is truly fixed, then the system should theoretically be insensitive to the starting initial guess.
Compute the initial conditions with different starting values.
| Out[142]= |  |
For certain systems, the computation of initial conditions is sensitive to the starting guess. To demonstrate, consider the following system.
For this problem with 
, the general solution is 
, so it is necessary to give 
to determine the solution. By using the default value of 
as the starting guess, the algorithm is forced to change the specified initial condition.
| Out[145]= |  |
The code essentially switches to a different solution branch.
| Out[146]= |  |
This happens because the default starting guess for the state 
is 1. During the Newton iterations, the system becomes singular because the second equation is identically satisfied and as a result the iterations diverge. To avoid complete failure, the algorithm is forced to modify the specified condition of 
.
To avoid this behavior, a "better" starting guess can be given. Using a starting guess of 
, the iterations converge to the expected consistent initial condition.
| Out[148]= |  |
| Out[149]= |  |
QR Method
The QR decomposition method is based on the work of Shampine [S02]. This algorithm is intended for index-1 or index-0 systems. The algorithm makes use of the efficient QR decomposition technique to decouple the system variables and their derivatives. In doing so, at each iteration step the solution of one system is broken down to two smaller systems of equations. For an 
-variable DAE system, the QR algorithm needs to handle at most a matrix of size 
as opposed to a matrix of size 
if the collocation method is used. In most cases, the algorithm only needs to handle matrices much smaller than 
. This makes the method quite efficient in handling very large systems. A brief description of the underlying algorithm is provided in this section.
Given an index-reduced system of the form 
, the system can first be linearized about an initial guess 
and 
as
.
A QR decomposition is performed on the Jacobian matrix 
such that 
, where 
is an orthogonal matrix, 
is an upper triangular matrix and 
is a permutation matrix. For DAEs, the matrix 
will not have a full row-rank. Depending on the rank of the matrix 
, the linearized system is then written as
.
The transformed system is solved in two steps:
.
Once the components are found, the transformed variables are converted back into the original form, using the permutation matrix, and the process is repeated until convergence.
The QR method can be called from the method 
, using Method->{"DAEInitialization"->{"QR", qropts}}, where qropts are options for the QR method.
| "DefaultStartingValue" | Automatic | starting value for unspecified components in the nonlinear iterations; option can be a one-element value  , or a list of two numbers  , where  are the starting values for the variable and its derivative, respectively |
| "MaxIterations" | 100 | maximum iterations |
Options for QR initialization.
Consider the pendulum example.
Given that this is a high-index DAE, an index reduction must be performed on the system. Once the system has been reduced to index 1/0, all the variables and their derivatives must be initialized.
Solve the pendulum DAE using automatic index reduction and the QR algorithm for initialization.
| Out[152]= |  |
| Out[153]= |  |
In the preceding example, the initial conditions are given such that they lead to a consistent set of starting values. In the event that the initial conditions are not consistent, the algorithm attempts to find consistent starting values.
Solve the pendulum DAE using the QR algorithm with inconsistent initial conditions.
| Out[154]= |  |
| Out[155]= |  |
Examine the modified initial conditions.
| Out[156]= |  |
| Out[157]= |  |
By specifying the option 
, the initial guess used for the iteration is changed. For inconsistent initial conditions, this may lead to a different consistent set.
Solve the pendulum DAE using QR and the option
.
| Out[159]= |  |
Examine the modified initial conditions obtained using a different starting guess.
| Out[160]= |  |
| Out[161]= |  |
BLT Method
The BLT method is based on transforming an index-reduced system into a block lower triangular form and then solving subsets of the system iteratively. The subsets themselves are solved using a Gauss-Newton method. This is sometimes advantageous because the index reduction algorithm that generates the index-reduced system tends to already have a block lower triangular form and it reduces the computational complexity by working with smaller subsystems with correspondingly smaller matrix computations. The algorithm also checks for inconsistent initial conditions and attempts to correct them.
The BLT method can be called from the method 
, using Method->{"DAEInitialization"->{"BLT", bltopts}}, where bltopts are options for the BLT method.
| "DefaultStartingValue" | Automatic | starting value for unspecified components in the nonlinear iterations; option can be a one-element value  , or a list of two numbers  , where  are the starting values for the variable and its derivative, respectively |
| "MaxIterations" | 100 | maximum iterations |
Options for BLT.
To see the advantage of using the BLT method, it is important to recognize that the index reduction algorithm leads to an expanded system of equations that are index 1 or index 0. Consider the following chemical systems example that describes an exothermic reaction.
The original DAE consists of four equations, while the index-reduced system consists of eight equations. The index-reduced equations are as follows.
Out[166]//MatrixForm= |
| |  |
Note that the expanded system now contains dummy derivatives. The expanded system can be analyzed further to see the structure of the system.
Generate an incidence matrix for the index-reduced system.
Out[170]//MatrixForm= |
| |  |
Find the block triangular ordering of the system.
Out[172]//TableForm= |
| |  |
This indicates that the expanded system can actually be solved sequentially. Therefore, rather than having one system of nine equations, a single equation can be solved sequentially. From an initialization perspective, setting t->0 would allow for the initialization of the variables.
Out[174]//TableForm= |
| |  |
This is the main principle behind the initialization using the BLT method. The BLT method is found to be especially useful and computationally efficient when dealing with large systems having a lower triangular form.
Solve the chemical system, using BLT for initialization.
| Out[176]= |  |
For cases with inconsistent initial conditions, the BLT method can suitably modify the initial conditions. It is, however, important to note that the results that obtained from the BLT method and the QR method may be different. Consider the pendulum example with inconsistent initial conditions.
Solve the pendulum DAE using the QR algorithm and inconsistent initial conditions.
| Out[180]= |  |
Solve the pendulum DAE using the BLT algorithm and inconsistent initial conditions.
| Out[182]= |  |
Inconsistent Initial Conditions
One of the main challenges in DAE system formulations and their solution is the fact that the starting initial conditions must be consistent. At the outset, this might seem straightforward, but for high-index DAE systems, you can easily encounter hidden conditions/equations that the initial conditions must also satisfy. If NDSolve encounters initial conditions that it finds to be inconsistent, it will attempt to correct them.
To illustrate the points about hidden constraints and inconsistent initial conditions, consider the pendulum system (2).
As a first case, consider when the initial conditions violate the algebraic constraint for the system. This is done by intentionally setting the initial condition for 
, so that it always violates the constraint 
.
Define inconsistent initial conditions.
If this system is given to NDSolve, an NDSolve::ivres message is generated, indicating that the initial conditions were found to be inconsistent. It then attempts to find a consistent initial condition using the inconsistent value as a starting guess for its iterations.
Find a consistent set of initial conditions using the inconsistent values as an initial guess.
Out[186]//TableForm= |
| |  |
Sometimes, it may not be clear if the specified conditions might be consistent or not. It may seem that the initial conditions satisfy the constraints, but may not satisfy the hidden constraint.
Specify initial conditions for the pendulum system.
These initial conditions satisfy the equation 
but fail to satisfy the implicit constraint 
. This constraint is not obvious because it is hidden and is only found by index reduction. The collocation algorithm does not perform index reduction and operates on the original equations. Even in the absence of an index-reduced system, the collocation algorithm is able to detect an inconsistency in the initial conditions and attempts to rectify it.
Obtain a consistent set of initial conditions.
Out[190]//TableForm= |
| |  |
DAE Reinitialization with Events
Consider a system of two equations with a discrete variable where a state change is made at 
.
Define the system variables and equations.
Solve the system with an event to do the state change.
| Out[195]= |  |
In the preceding example, initial conditions for 
and 
are given. The initialization code automatically computes the consistent initial condition 
. At time 
, an event is triggered that says that the discrete variable should be changed from 1 to 2. At time 
, a reinitialization of the variables needs to take place. The variable 
is called a modified variable. The following strategy is adopted during reinitialization:
1. Keep all the state, discrete, and modified variables fixed. If a state variable has a derivative fixed (or specified to be changed), then that variable can be changed.
2. If strategy 1 fails to reinitialize, then keep the state variables and modified variables fixed and allow other variables and their derivatives to change.
3. If strategy 2 fails, then the modified variables and the state variables with derivatives in the DAE are kept fixed. All other variables and their derivatives can be changed.
4. If strategy 3 fails, then only the modified variables are kept fixed and all the state variables and their derivatives are allowed to change.
Just before the reinitialization, the values of 
, 
, and 
are as follows.
Get the values just before the event at
.
| Out[196]= |  |
Based on the outlined strategy, at time 
, using strategies 1 and 2, it is required that 
, 
, and 
do not change. Given that 
, this clearly violates the algebraic equation 
. Strategies 1 and 2 therefore fail.
Strategy 3 requires that variables with derivatives should not change. Therefore 
is kept fixed (along with 
) and 
is allowed to change. This modifies the value of 
as shown in the plot (the blue line).
Get the reinitialized values just after the event at
.
| Out[197]= |  |
WhenEvent allows for simultaneous and sequential evaluation of event actions, including state changes.
After each state change, even for the same event, the DAE is reinitialized using the preceding strategy, so if possible, it is more efficient to just give one rule for the state changes needed. The final state when there are multiple state changes done at the same event time may be different because the new values are used in each subsequent evaluation and setting and for DAEs these values may depend on the reinitialization. Consider the previous problem with additional events.
Solve the problem with three rules given for the state changes that will be evaluated in sequence.
| Out[199]= |  |
To see why the solution is different from the one preceding, it is necessary to follow the sequence of settings. First 
is set to 2 and the DAE is reinitialized before evaluating the other settings. This reinitialization changes the value of 
to 2 since that is how the strategy finds a solution consistent with the residual. Execution of the second action sets 
to 2 (the current value of 
), but this is inconsistent with the residual, so since 
is an algebraic variable its value is set to 4 (
). Finally, setting 
to 
resets 
to 2, and to avoid modifying the newly set algebraic variable, the value of 
is reset to 1.
One way to see the sequence of changes is to put in Print commands between the settings.
Print the variable values between settings.
| Out[201]= |  |
Solve switching the last two settings.
| Out[203]= |  |
So a different sequence of settings leads to a different solution.
With a single rule there is only one initialization, so if all of the variables are set, the values given should be consistent or reinitialization strategy may fail or not give the expected values.
Attempt to set all variables to values inconsistent with the DAE using a single rule.
| Out[204]= |  |
Here 
, 
, and 
are fixed. This is a very restrictive constraint, and all the strategies fail.
Setting a variable to its current value within a single rule in effect forces it to stay the same.
Change
to 2 and force
to remain the same at
.
| Out[206]= |  |
Since 
stays the same 
is forced to change.
DAE Examples
Torus Problem
This is a test problem taken from Campbell and Moore [CM95]. The DAE describes the motion of a particle in 3D. This is an index 3 DAE with three position variables, three velocity variables, and one constraint. The solution manifold is four dimensional, and the exact solution is given by
.
Define parameters and functions to use for the solution.
Define the system equations and variables.
An exact solution is known.
| Out[214]= |  |
Solve and visualize the system.
| Out[215]= |  |
| Out[216]= |  |
Compare the solution between the analytic and computed solution.
| Out[218]= |  |
Discharge of Pressure from a Tank
This is a simplified model of a dynamic process in petrochemical engineering. The details of this model can be found in Hairer et. al. [HLR89]. This is an index 2 system.
Define the parameters for the system.
Define the equations and the variables.
Solve and visualize the solution.
| Out[223]= |  |
| Out[224]= |  |
Non-flexible Slider Crank
This example is a simple constrained multibody system. The system consists of a crank of mass 
, which is hinged on a fixed surface, a slider of mass 
, and a connecting rod of mass 
. The slider is constrained to move only in the horizontal plane. Due to the masses of the individual components, the moments of inertia would have to be considered during the construction of the system. A schematic of the problem is shown following. The system can be completely defined using the two angles.
The state of the slider-crank mechanism can be described completely by two angles 
and the distance 
of the slider from origin.
Define the force that is exerted on the slider.
The equations of motion are derived by resolving the forces and applying Newton's law 
and 
. The crank and connecting rod have mass and therefore inertia.
Define the differential system,
The algebraic equations define the geometry of the system.
Define the physical parameters for the system. Here
and
are the moment of inertia.
Solve and visualize the system.
| Out[23]= |  |
Define functions for animatiing slider crank.
Animate the motion of the system.
| Out[87]= |  |
Slider-Crank with Spring Damper Attaching the Links.
This is an extension of the simple slider crank mechanism. A spring and damper system is attached between the crank and the connecting rod. This spring constrains the range of motion of the crank, while the damper slowly brings the system to a steady state. The schematic of the system is given following.
The state of the slider-crank mechanism can be described completely by two angles 
and the distance 
of the slider from origin.
Define the force that is exerted on the slider.
The equations of motion are derived by resolving the forces and applying Newton's law 
and 
. The crank and connecting rod have mass and therefore inertia.
Define the differential system.
Define the algebraic constraints.
Define the parameters for the system.
Solve and visualize the system
| Out[75]= |  |
Define functions for generating the animation
Animate the motion of the slider crank system with a spring and damper. Due to the damper and spring, the motion eventually comes to rest in the horizontal plane.
| Out[109]= |  |
Two-Link Planar Robotic Arm
The two-link planar robotic arm is a frictionless, constrained mechanical system. The system consists of two links attached to each other through a joint, such that one end of the first link is held fixed, while the trajectory at the end of the second link is specified. The following figure shows a schematic of the system.
The system can be completely defined using the angles between the links. Additional details of this system can be found in Ascher et. al. [ACPR94].
Define the trajectory that the end of the robot arm must follow. This corresponds to defining the position of
The motion is a
The equations of motion are derived by resolving the forces and applying Newton's law. The differential equations are derived for the angles. The Cartesian coorinates 
and 
are therefore represented in terms of the angle.
Define the differential equations.
Define the parameters associated with the system.
Solve and visualize the system.
| Out[163]= |  |
| Out[164]= |  |
Animate the motion of the robotic arm constrained to move on a specified curve
| Out[187]= |  |
N-Pendulum Problem
Construct a function for generating a n-pendulum system.
Generate a two pendulum system
Solve and visualize the pendulum system
| Out[282]= |  |
Visualize the chaotic trajectory of the second pendulum rod
| Out[283]= |  |
Transistor Amplifier Circuit
Define the parameters for the transistor-amplifier circuit.
Solve and visualize the DAE system
| Out[295]= |  |
Akzo-Nobel Chemical Reaction
The following system describes a chemical process in which two species, FLB and ZHU, are mixed while 
is constantly added to the system. The chemical names are fictitious. Details of the system and the dynamics associated with it can be found in [N93]. The reaction equations follow. Associated with each reaction, there are rates of reaction, which are specified. The algebraic constraint comes from the last reaction, which requires FLB and ZHU and its mixture to maintain a constant relationship.
Define the reaction rates and the parameters of the chemical reaction
Generate the rate equations for the system
Solve and visualize the system
| Out[307]= |  |
Car-Axis problem
The car-axis model is a simple multibody system that is designed to simulate the behavior of a car axis on a bumpy road. A schematic of the system is shown following. The model consists of two wheels: the left wheel is assumed to be moving on a flat surface, while the right wheel moves over a bumpy surface. The bumpy surface is modeled as a sinusoid. The left and right wheels transfer their motion to the chassis of the car through two massless springs as shown following. The chassis of the car is modeled as a bar of mass M. Additional details of this model can be found in Mazzia et. al. [MM08]. This is an index 3 system.
The left tire at is always on a flat surface while the right tire periodically goes over a bump.
Define the motion of the right wheel as it goes over the bump.
The distance between the wheels must always remain fixed and the car chassis must always have a fixed length.
Derive the equations of motion using Newton's law.
Define the parameters associated with the system.
Solve and visualize the solution.
| Out[209]= |  |
Combined Elliptic-Parabolic PDE in 1D
The following is a synthetic example for solving a parabolic and an elliptic PDE that are coupled together in a nonlinear fashion. Spatial discretization of the PDEs results in a system that contains a significant number of algebraic variables. The equations are set up such that the analytic solution exists for the system. The details of the coupled system are given following.
Discretizing the spatial component of the PDE using method of lines and construct a system of ODEs from the governing equations. These form the differential equations.
Specify the boundary conditions for the system. These form the algebraic equations of the system.
Specify the initial conditions of the system
Solve the PDE as a DAE system
| Out[236]= |  |
Multispecies Food Web Model (Combined Elliptic-Parabolic PDE in 2D)
This example is a model of the multispecies food web [B86]. Unlike the typical predatory-prey problem, there is a spatial component of this problem. The predator-prey relationships are defined over a 2D spatial domain via a series of diffusion parameters. The general coupled PDE is given by
In this system, the first 
species are the prey and the next 
species are the predators. The specific case of 
is considered here. This means that there is one predator and one prey species. The spatial domain is discretized with a 20×20 mesh. This means that there are 2×400 variables in the final DAE system. A uniform distribution of the predators is specified initially. This is leads to a inconsistent initial condition that is corrected by the built-in algorithms.
Define the parameters needed for the model
Generate the finite difference differentiation matrices for the first and second derivatives. Generate the Laplacian matrix from it.
Define the species in the food web.
Generate the equations for the model.
Define the initial conditions for the model.
Simulate the food web model
Plot of the corrected/modified initial conditions. They predator distributions are changed.
| Out[204]= |  |
Visualization of the solution at
and
.
| Out[206]= |  |
| Out[208]= |  |
Animation of the evolution of the solution over time shows that a steady state is reached quite fast for the given parameters.
| Out[209]= |  |
Andrews's Squeezer Mechanism
The Andrews squeezer mechanism is a multibody system containing seven different links. The dimensions of the various links and their specifications are given following. The system can be completely defined using seven angles. The angles are labeled 
-
in the following system. Additionally, there are six algebraic constraints associated with the link dimensions and connections. This leads to a 14-dimensional, index 3 system. Details of the system can be found in Hairer and Wanner [HW96].
The dimensions associated with the various links are shown below. The seven links are labeled 
.
The notation for the parameters used in the model and their description can be found in Hairer and Wanner [HW96].
Clear some of the parameters.
The motion of the system can be defined using seven angles. The angles are defined as 
here. The equations of motion can be derived using Hamiltonian principles resulting in a a system of equations of the form 
where 
is a mass matrix, 
is a vector of forces, 
is a vector of constraints, and 
are Lagrange multipliers.
Define the variables for angles and Largrange multipliers.
Define the mass matrix
associated with the system.
Define the various forces
associated with the system.
Define the constraint vector
associated with the various links.
Construct the equations
and the constraint equations with particular values of the parameters.
Define the initial state of the system to be at rest with a particular set of angles.
Solve the system and plot the angles and the forces. The motion of the links becomes faster as time progresses. The lines are color coded based on the color of the links.
| Out[33]= |  |
| Out[34]= |  |
Visualize the motion of the mechanism.
| Out[35]= |  |
