Working with String Patterns
Introduction
The general symbolic string patterns in Mathematica allow you to perform powerful string manipulation efficiently. What follows discusses the details of string patterns, including usage and implementation notes. The emphasis is on issues not mentioned elsewhere in the help system.
At the heart of
Mathematica is a powerful language for describing patterns in general expressions. This language is used in function definitions, substitutions, and searches, with constructs like
,
,
, and so on.
| Out[1]= |  |
| Out[2]= |  |
| Out[3]= |  |
A
Mathematica string pattern uses the same constructs to describe patterns in a text string. You can think of a string as a sequence of characters and apply the principles of general
Mathematica patterns. In addition there are several useful string-specific pattern constructs.
| Out[4]= |  |
| Out[5]= |  |
| Out[6]= |  |
Regular expressions can be used as an alternative way to specify string patterns. These tend to be more compact, but less readable.
| Out[7]= |  |
| Out[8]= |  |
| Out[9]= |  |
Here is a list of several functions that recognize string patterns.
| StringMatchQ["s",patt] | test whether s matches patt |
| StringFreeQ["s",patt] | test whether s is free of substrings matching patt |
| StringCases["s",patt] | give a list of the substrings of s that match patt |
| StringCases["s",lhs->rhs] | replace each case of lhs by rhs |
| StringPosition["s",patt] | give a list of the positions of substrings that match patt |
| StringCount["s",patt] | count how many substrings match patt |
| StringReplace["s",lhs->rhs] | replace every substring that matches lhs |
| StringReplaceList["s",lhs->rhs] | give a list of all ways of replacing lhs |
| StringSplit["s",patt] | split s at every substring that matches patt |
| StringSplit["s",lhs->rhs] | split at lhs, inserting rhs in its place |
Functions that support string patterns.
General String Patterns
A general string pattern is formed from pattern objects similar to the general pattern objects in
Mathematica. To join several string pattern objects, use the
StringExpression operator
.
Out[10]//FullForm= |
| |  |
StringExpression is closely related to
StringJoin, except nonstrings are allowed and lists are not flattened. For pure strings, they are equivalent.
| Out[11]= |  |
The list of objects that can appear in a string pattern closely matches the list for ordinary Mathematica patterns. In terms of string patterns, a string is considered a sequence of characters, that is, 
can be thought of as something like String[a, b, c], to which the ordinary pattern constructs apply.
The following objects can appear in a symbolic string pattern:
| "string" | a literal string of characters |
| _ | any single character |
| __ | any substring of one or more characters |
| ___ | any substring of zero or more characters |
| x_,x__,x___ | substrings given the name x |
| x:pattern | pattern given the name x |
| pattern.. | pattern repeated one or more times |
| pattern... | pattern repeated zero or more times |
| {patt1,patt2,...} or patt1|patt2|... | a pattern matching at least one of the  |
| patt/;cond | a pattern for which cond evaluates to True |
| pattern?test | a pattern for which test yields True for each character |
| Whitespace | a sequence of whitespace characters |
| NumberString | the characters of a number |
| DatePattern[spec] | the characters of a date |
| charobj | an object representing a character class (see below) |
| RegularExpression["regexp"] | substring matching a regular expression |
| StringExpression[...] | an arbitrary string expression |
The following represent classes of characters:
The following represent positions in strings:
The following determine which match will be used if there are several possibilities:
| Shortest[p] | the shortest consistent match for p |
| Longest[p] | the longest consistent match for p (default) |
Some nontrivial issues regarding these objects follow.
The
,
, and
wildcards match any characters including newlines. To match any character except newline (analogous to the "." in regular expressions), use
Except["\n"],
Except["\n"].., and
Except["\n"]....
| Out[12]= |  |
| Out[13]= |  |
| Out[14]= |  |
A list of patterns, such as
, is equivalent to a list of alternatives, such as
. This is convenient in that functions like
Characters and
CharacterRange can be used to specify classes of characters.
| Out[15]= |  |
When
Condition (
) is used, the patterns involved are treated as strings as far as the rest of
Mathematica is concerned, so you need to use
ToExpression in some cases.
| Out[16]= |  |
Similar to ordinary
Mathematica patterns, the function in
PatternTest (
) is applied to each individual character.
| Out[17]= |  |
| Out[18]= |  |
| Out[19]= |  |
This inserts a lookbehind constraint (see
"Regular Expressions") to ensure that you only pick words preceded by
.
| Out[20]= |  |
| Out[21]= |  |
The Except construct for string patterns takes a single argument that should represent a single character or a class of single characters.
This deletes all nonvowel characters from the string.
| Out[22]= |  |
When trying to match patterns of variable length (such as
and
), the longest possible match is tried first by default. To force the matcher to try the shortest match first, you can wrap the relevant part of the pattern in
Shortest[ ].
| Out[23]= |  |
| Out[24]= |  |
If for some reason you need a longest match within the short match, you can use
Longest.
| Out[25]= |  |
| Out[26]= |  |
You could alternatively rewrite this pattern without use of
Longest.
| Out[27]= |  |
Regular Expressions
The regular expression syntax follows the underlying Perl Compatible Regular Expressions (PCRE) library, which is close to the syntax of Perl. (See [1] for further information and documentation.) A regular expression in Mathematica is denoted by the head RegularExpression.
The following basic elements can be used in regular expression strings:
| c | the literal character c |
| . | any character except newline |
| [c1c2...] | any of the characters  |
| [c1-c2] | any character in the range  - |
| [^c1c2...] | any character except the  |
| p* | p repeated zero or more times |
| p+ | p repeated one or more times |
| p? | zero or one occurrence of p |
| p{m,n} | p repeated between m and n times |
| p*?,p+?,p?? | the shortest consistent strings that match |
| p*+,p++,p?+ | possessive match |
| (p1p2...) | strings matching the sequence  ,  , ... |
| p1|p2 | strings matching  or  |
The following represent classes of characters:
| \\d | digit 0-9 |
| \\D | nondigit |
| \\s | space, newline, tab, or other whitespace character |
| \\S | non-whitespace character |
| \\w | word character (letter, digit, or  ) |
| \\W | nonword character |
| [[:class:]] | characters in a named class |
| [^[:class:]] | characters not in a named class |
The following named classes can be used: alnum, alpha, ascii, blank, cntrl, digit, graph, lower, print, punct, space, upper, word, and xdigit.
The following represent positions in strings:
| ^ | the beginning of the string (or line) |
| $ | the end of the string (or line) |
| \\A | the beginning of the string |
| \\z | the end of the string |
| \\Z | the end of the string (allowing for a single newline character first) |
| \\b | word boundary |
| \\B | anywhere except a word boundary |
The following set options for all regular expression elements that follow them:
| (?i) | treat uppercase and lowercase as equivalent (ignore case) |
| (?m) | make  and  match start and end of lines (multiline mode) |
| (?s) | allow  to match newline |
| (?x) | disregard all whitespace and treat everything between  and  as comments |
| (?-\#c) | unset options |
The following are lookahead/lookbehind constructs:
| (?=p) | the following text must match p |
| (?!p) | the following text cannot match p |
| (?<= p) | the preceding text must match p |
| (?<!p) | the preceding text cannot match p |
Discussion of a few issues regarding regular expressions follows.
This looks for runs of word characters of length between 2 and 4.
| Out[28]= |  |
With the possessive
quantifier, as many characters as possible are grabbed by the matcher, and no characters are given up, even if the rest of the patterns require it.
| Out[29]= |  |
| Out[30]= |  |
| Out[31]= |  |
corresponds to characters in a hexadecimal number.
| Out[32]= |  |
The complete list of characters that need to be escaped in a regular expression consists of 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, and 
. For instance, to write a literal period, use 
and to write a literal backslash, use 
.
Inside a character class 
, the complete list of escaped characters is 
, 
, 
, 
, and 
.
By default,
and
match the beginning and end of the string, respectively. In multiline mode, these match the beginning/end of lines instead.
| Out[33]= |  |
| Out[34]= |  |
In multiline mode,
and
can be used to denote the beginning and end of the string.
| Out[35]= |  |
The
modifier allows you to add whitespace and comments to a regular expression for readability.
| Out[36]= |  |
Named subpatterns are achieved by surrounding them with parentheses
(subpatt); they then become numbered subpatterns. The number of a given subpattern counts the opening parenthesis, starting from the start of the pattern. You can refer to these subpatterns using
\\n for the
n
pattern later in the pattern, or by
in the right-hand side of a rule.
refers to all of the matched pattern.
| Out[37]= |  |
| Out[38]= |  |
If you need a literal
in this context (when the head of the left-hand side is
RegularExpression), you can escape it by using backslashes (for example,
).
| Out[39]= |  |
If you happen to need a single literal backslash followed by a literal
under these circumstances, you need to be a bit tricky and split into two strings temporarily.
| Out[40]= |  |
If you need to group a part of the pattern, but you do not want to count the group as a numbered subpattern, you can use the
construct.
| Out[41]= |  |
Lookahead and lookbehind patterns are used to ensure a pattern is matched without actually including that text as part of the match.
This picks out words following the string
.
| Out[42]= |  |
This tries to pick out all even numbers in the string, but it will find matches that include partial numbers.
| Out[43]= |  |
Using lookbehind/lookahead, you can ensure that the characters before/after the match are not digits (note that the lookbehind test is superfluous in this particular case).
| Out[44]= |  |
RegularExpression versus StringExpression
There is a close correspondence between the various pattern objects that can be used in general symbolic string patterns and in regular expressions. Here is a list of examples of patterns written as regular expressions and as symbolic string patterns.
| | |
| "abc" | "abc" | the literal string  |
| "." | Except["\n"] | any character except newline |
| "(?s)." | _ | any character |
| "(?s).+" | __ | one or more characters (greedy) |
| "(?s).+?" | Shortest[__] | one or more characters (nongreedy) |
| "(?s).*" | ___ | zero or more characters |
| ".*" | Except["\n"]... | zero or more characters (except newlines) |
| "a?b" | "a"|""~~"b" | zero or one  followed by a  (that is,  or  ) |
| "[abef]" | Characters["abef"] | any of the characters  ,  ,  , or  |
| "[abef]+" | Characters["abef"].. | one or more of the characters  ,  ,  , or  |
| "[a-f]" | CharacterRange["a","f"] | any character in the range between  and  |
| "[^abef]" | Except[Characters["abef"]] | any character except the characters  ,  ,  , or  |
| "ab|efg" | "ab"|"efg" | match the strings  or  |
| "(ab|ef)gh"or"(?:ab|ef)gh" | ("ab"|"ef")~~"gh" |  or  followed by  (that is,  or  ) |
| "\\s" | WhitespaceCharacter | any whitespace character |
| "\\s+" | Whitespace | one or more characters of whitespace |
| "(a|b)\\1" | x:"a"|"b"~~x_ | this will match either  or  |
| "\\d" | DigitCharacter | any digit character |
| "\\D" | Except[DigitCharacter] | any nondigit character |
| "\\d+" | DigitCharacter.. | one or more digit characters |
| "\\w" | WordCharacter|"_" | any digit, letter, or  character |
| "[[:alpha:]]" | LetterCharacter | any letter character |
| "[^[:alpha:]]" | Except[LetterCharacter] | any nonletter character |
| "^abf"or"\\Aabc" | StartOfString~~"abf" | the string  at the start of the string |
| "(?m)^abf" | StartOfLine~~"abf" | the string  at the start of a line |
| "wxz$"or"wxz\\z" | "wxz"~~EndOfString | the string  at the end of the string |
| "wxz\\Z" | "wxz"~~"\n"|""~~EndOfString | the string  at the end of the string or before newline at the end of the string |
Pattern objects that can be used in general string patterns, but not in regular expressions, include conditions (
) and pattern tests (
) that can access general Mathematica code during the match.
Some special constructs in regular expressions are not directly available in general string patterns. These include lookahead/lookbehinds and repeats of a given length. They can be embedded into a larger general string pattern by inserting a RegularExpression object.
String Manipulation Functions
The following discusses some particulars and subtleties in the various string manipulation functions (see the reference pages for more information on these functions).
StringMatchQ
StringMatchQ is used to check whether a whole string matches a certain pattern.
| Out[45]= |  |
| Out[46]= |  |
StringMatchQ is special in that it also allows the metacharacters 
and 
to be entered as wildcards (for backward compatibility reasons). 
is equivalent to Shortest[___] (RegularExpression["(?s).*?"]) and 
is equivalent to Except[CharacterRange["A", "Z"]] (RegularExpression["[^A-Z]"]).
The following three patterns are therefore equivalent.
| Out[47]= |  |
| Out[48]= |  |
| Out[49]= |  |
Note that technically the appearance of Shortest does not make a difference here, since we are only looking for a possible match.
If you need to access parts of the string matched by subpatterns in the pattern, use StringCases instead.
StringMatchQ has a
SpellingCorrection option for finding matches allowing for a small number of discrepancies. This only works for patterns consisting of a single literal string.
| Out[50]= |  |
StringFreeQ
StringFreeQ is used to check whether a string contains a substring matching the pattern. You cannot extract the matching substring; to do this you would use
StringCases.
| Out[51]= |  |
| Out[52]= |  |
StringCases
StringCases is a general purpose function for finding occurrences of patterns in a string, picking out subpatterns, and processing the results.
Find substrings matching a pattern.
| Out[53]= |  |
Pick apart the matching substring.
| Out[54]= |  |
| Out[55]= |  |
Restrict the number of matches.
| Out[56]= |  |
You can use a list of rules.
| Out[57]= |  |
| Out[58]= |  |
| Out[59]= |  |
The Overlaps Option
The Overlaps option for StringCases, StringPosition, and StringCount deals with how the matcher proceeds after finding a match. It has three possible settings: False, True, or All. The default is False for StringCases and StringCount, while it is True for StringPosition.
With
Overlaps->False, the matcher continues the match testing at the character following the last matched substring.
| Out[60]= |  |
With
Overlaps->True, the matcher continues at the character following the first character of the last matched substring (when a single pattern is involved).
| Out[61]= |  |
With
Overlaps->All, the matcher keeps starting at the same position until no more new matches are found.
| Out[62]= |  |
If multiple patterns are given in a list,
Overlaps->True will cause the matcher to start at the same position once for each of the patterns before proceeding to the next character.
| Out[63]= |  |
| Out[64]= |  |
Note that with
Overlaps->True, there can thus be a difference between specifying a list of patterns and using the alternatives operator (
).
| Out[65]= |  |
| Out[66]= |  |
StringPosition
| Out[67]= |  |
| Out[68]= |  |
| Out[69]= |  |
Note that even empty strings can be matches.
| Out[70]= |  |
StringCount
StringCount returns the number of matching substrings (which are found by
StringPosition or
StringCases). It is useful for cases with many matches where memory for storing all the substrings might be an issue.
| Out[71]= |  |
| Out[72]= |  |
Note that Overlaps->False is the default for StringCount.
StringReplace
StringReplace is used for substituting substrings matching the given patterns.
| Out[73]= |  |
Named patterns can be used as strings on the right-hand side of the replacement rules. Note the use of
RuleDelayed (
) to avoid premature evaluation.
| Out[74]= |  |
When using regular expressions, it is convenient to remember that
on the right-hand side refers to the whole matched substring.
| Out[75]= |  |
You can limit the number of replacements made by specifying a third argument.
| Out[76]= |  |
Note that the replacement does not have to be a string. If the result is not a string, a
StringExpression is returned.
| Out[77]= |  |
Out[78]//FullForm= |
| |  |
There is limited support for using the old 
option in conjunction with general string patterns, but this option is deprecated and its use should be avoided.
StringReplaceList
StringReplaceList returns a list of strings where a
single string replacement has been made in all possible ways.
| Out[79]= |  |
If a list of strings is given as input, the output is a nested list of results.
| Out[80]= |  |
StringSplit
StringSplit is useful for splitting a string into many strings at delimiters matching a pattern. By default, the splits happen at runs of whitespace.
| Out[81]= |  |
For instance, to split a normal sentence into words, you need to also include punctuation in the delimiter.
| Out[82]= |  |
By default, empty strings at the beginning and the end of the result are removed.
| Out[83]= |  |
These can be included by specifying
All as a third argument.
| Out[84]= |  |
The third argument can also be a number giving the maximum number of strings to split into.
| Out[85]= |  |
This splits a string into individual lines.
| Out[86]= |  |
You can also split at patterns that match positions, such as
StartOfLine. This keeps the newline characters in the result.
| Out[87]= |  |
You can keep the delimiters, or parts of the delimiters, in the output by using a rule as the second argument.
| Out[88]= |  |
| Out[89]= |  |
| Out[90]= |  |
| Out[91]= |  |
You can give a list of patterns and rules as well; the delimiters matching the patterns will be left out of the result.
Out[92]//InputForm= |
| |  |
For Perl Users
Overview
With the addition of general string patterns, Mathematica can be a powerful alternative to languages like Perl and Python for many general, everyday programming tasks. For people familiar with Perl syntax, and the way Perl does string manipulation, the following rough guide shows how to get similar functionality in Mathematica.
Here is an overview of the Mathematica functions involved in constructing Perl-like functions.
| | |
| m/.../ | StringFreeQ or StringCases | match a string with a regular expression, possibly extracting subpatterns |
| s/.../.../ | StringReplace | replace substrings matching a regular expression |
| split(...) | StringSplit | split a string at delimiters matching a regular expression |
| tr/.../.../ | StringReplace | replace characters by other characters |
| /i | IgnoreCase->True or "(?i)" | case-insensitive modifier |
| /s | "(?s)" | force  to match all characters (including newlines) |
| /x | "(?x)" | ignore whitespace and allow extended comments in regular expression |
| /m | "(?m)" | multiline mode ( and  match start/end of lines) |
Following are some common Perl constructs in more detail.
m/.../
The match operator 
tests whether a string contains a substring matching the 
. For simple matches of this sort in Mathematica, use StringFreeQ.
Here is a Perl snippet for testing whether a string contains a
somewhere after an
.
$string = "sdakdb";
if ($string =~ m/a.*b/){
print "Match!";
}
Here is a
Mathematica version of the same test.
If parts of the matched string need to be accessed later, using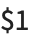 
, 
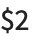, ... in Perl, the best Mathematica function to use is normally StringCases.
Here is Perl code for extracting an error message.
$res = "ERROR = paper jam";
if ($res =~ m/ERROR = (.*)/){
print "Hey, you should check the $1!";
}
Here is a
Mathematica version.
Here is Perl code for extracting several subpatterns at once.
$date = "88/6/13";
($year, $month, $day) = $date =~ m/^(\d+)/(\d+)/(\d+)$/;
| Out[98]= |  |
This is similar to assigning all the matches to an array using the
modifier.
$text = "128.32.13.117";
@nums = $text =~ m/\d+/g;
The same thing is easily done with
StringCases in
Mathematica.
| Out[100]= |  |
s/.../.../
The obvious
Mathematica version of the Perl
substitution operator is
StringReplace.
$text = "abcagh";
$text =~ s/a./XX/;
The default Perl behavior is to do a single replacement.
| Out[102]= |  |
The
modifier in Perl does global replacement of all matches.
| Out[103]= |  |
Using the evaluation
modifier, Perl can use subpatterns as part of the replacement. This is easily done in
Mathematica.
$text = "13 27 3";
$text =~ s/(\d+)/$1$1/eg
| Out[105]= |  |
split(...)
The Perl
command is similar to
StringSplit in
Mathematica.
$text = "ab:cd:efg";
split(/:/, $text)
| Out[107]= |  |
You can specify the number of blocks to split into in both Perl and
Mathematica.
| Out[108]= |  |
A
with capturing parentheses in the pattern, for which the captured substrings are included in the result, can be done in
Mathematica using rules in the second argument of
StringSplit. Compared to Perl, in
Mathematica it is easy to then apply a function to these substrings.
$text = "test with <tag1>tags</tag1> and <b>more</b>";
split(/<([^>]*)>/, $text)
Out[110]//InputForm= |
| |  |
Out[112]//InputForm= |
| |  |
tr/.../.../
The Perl 
command can be simulated using Mathematica StringReplace together with the appropriate list of rules.
Here is the simplest form where the characters
,
, and
are replaced by
,
, and
, respectively.
$text = "abcdef";
$text =~ tr/abc/XYZ/
This generates the appropriate rules in
Mathematica using
Thread.
| Out[114]= |  |
Here is an example where the replacement list is shorter than the character list, so
,
, and
are all replaced by
.
$text = "abcdefghi";
$text =~ tr/abcdef/WXYZ/
| Out[116]= |  |
Character ranges in Perl are emulated using
CharacterRange in
Mathematica.
$text = "this and that";
$text =~ tr/a-z/x/
| Out[118]= |  |
With the
modifier, the surplus characters are instead deleted.
$text = "abcdefghi";
$text =~ tr/abcdef/WXYZ/d
| Out[120]= |  |
With the
modifier, the complement of the character list is used.
| Out[121]= |  |
| Out[122]= |  |
The
modifier squeezes down to one any run of characters translating into the same character.
$text = "abbcccddddeeeeeeffeeded";
$text =~ tr/abcde/ABCD/s
You get the same effect in
Mathematica using
Repeated (
).
| Out[124]= |  |
Some Examples
Some brief examples of practical uses of string patterns are presented in this section.
Highlight Patterns
This defines a 1000-base random DNA string.
| Out[125]= |  |
This highlights parts of the DNA that match a certain pattern.
| Out[126]= |  |
Here is the same result using a regular expression.
| Out[127]= |  |
HTML Parsing
String patterns are useful for taking raw HTML and extracting information from it.
| Out[129]= |  |
This extracts all the direct hyperlinks in the source.
| Out[130]= |  |
This deletes everything inside tags
<...>.
| Out[131]= |  |
Find Money
Here is some text to scan for strings that look like dollar amounts.
| Out[132]= |  |
This is one way to do the search using symbolic string patterns.
| Out[133]= |  |
Here is the same search using regular expressions (note that you must remember to escape the dollar sign).
| Out[134]= |  |
There is also a built-in pattern object,
NumberString, for this particular situation.
| Out[135]= |  |
Find Text in Files
Here is a very simple grep-like function for finding lines in a text file containing text matching a given pattern.
This creates a sample text file.
| Out[137]= |  |
This returns the line numbers and lines in
containing any digit characters.
Out[138]//TableForm= |
| |  |
This finds lines containing
as a standalone word.
Out[139]//TableForm= |
| |  |
Tips and Tricks for Efficient Matching
This section addresses some issues involving efficiency in string pattern matching.
StringExpression versus RegularExpression
Since a string pattern written in Mathematica syntax is immediately translated to a regular expression and then compiled and cached, there is very little overhead in using the Mathematica syntax as opposed to the regular expression syntax directly. An exception to this happens when many different patterns are used a few times; in that case the overhead might be noticeable.
Conditions and PatternTests
If a pattern contains
Condition (
) or
PatternTest (
) statements, the general
Mathematica evaluator must be invoked during the match, thus slowing it down. If a pattern can be written without such constructs, it will typically be faster.
| Out[141]= |  |
| Out[142]= |  |
Avoid Nested Quantifiers
Because of the nondeterministic finite automaton (NFA) algorithm used in the match, patterns involving nested quantifiers (such as 
and 
or the regular expression equivalents) can become arbitrarily slow. Such patterns can usually be "unrolled" into more efficient versions (see Friedl [2] for additional information).
Avoid Many Calls to a Function
If you are searching through a long list of strings for certain matches, it is more efficient to feed the whole list to a string function at once, rather than using something like
Select and
StringMatchQ (see the earlier dictionary example for an illustration). Here is another example that generates a list of 2000 strings with 10 characters each and searches for the strings that start with an
and contain
as a substring.
| Out[144]= |  |
| Out[145]= |  |
If you instead feed the whole list to
StringMatchQ at once, it will be much faster. Then
Pick can be used to extract the wanted elements.
| Out[146]= |  |
Alternatively, you could use
StringCases, which is also fast. Note that you need to anchor the pattern using
StartOfString to ensure that the
is at the start (the
EndOfString is superfluous in this particular case).
| Out[147]= |  |
Rewrite General Expression Searches as String Searches
Because the string-matching algorithm is different than the algorithm Mathematica uses for general expression matching (string matching can assume a finite alphabet and a flat structure, for instance), there are cases where it is advantageous to translate a normal expression-matching problem to a string-matching problem. A typical case is matching a long list of symbols against a pattern involving several occurrences of 
and 
.
As an example, assume you want to find primes (after prime number 1000000, say) that have at least four identical digits. Using ordinary pattern matching, it could be accomplished like this.
| Out[148]= |  |
By converting the list of integers to a string, you can use string matching instead.
| Out[149]= |  |
By using the previous tips of using
Pick or
StringCases, you can speed it up even more.
| Out[150]= |  |
| Out[151]= |  |
For long sequences, the difference can be significant.
| Out[153]= |  |
| Out[154]= |  |
| Out[156]= |  |
| Out[157]= |  |
Implementation Details
String pattern matching in Mathematica is built on top of the PCRE (Perl Compatible Regular Expressions) library by Philip Hazel [1].
In some cases the pre-5.1 Mathematica algorithms are used (for example, when the pattern is just a single, literal string).
Any symbolic string pattern is first translated to a regular expression. You can see this translation by using the internal
function.
Out[158]//InputForm= |
| |  |
The first element returned is the regular expression, while the rest of the elements have to do with conditions, replacement rules, and named patterns.
The regular expression is then compiled by PCRE, and the compiled version is cached for future use when the same pattern appears again. The translation from symbolic string pattern to regular expression only happens once.
Mathematica conditions in the pattern are handled by external call-outs from the PCRE library to the Mathematica evaluator, so this will slow down the matching.
Explicit RegularExpression objects embedded into a general string pattern will be spliced into the final regular expression (surrounded by noncapturing parentheses 
), so the counting of named patterns can become skewed compared to what you might expect.
Because PCRE currently does not support preset character classes with characters beyond character code 255, the word and letter character classes (such as WordCharacter and LetterCharacter) only include character codes in the Unicode range 0-255. Thus LetterCharacter and _?LetterQ do not give equivalent results beyond character code 255.
Because of a similar PCRE restriction, case-insensitive matching (for example, with IgnoreCase->True) will only apply to letters in the Unicode range 0-127 (that is, the normal English letters 
-
and 
-
).
References
[1] Hazel, P. "PCRE—Perl Compatible Regular Expressions." 2004. www.pcre.org
[2] Friedl, J. E. F. Mastering Regular Expressions, 2nd ed. O'Reilly & Associates, 2002.
to 
