3.12.1 NonlinearSetup

Command structure of NonlinearSetup.

Before applying the nonlinear simplification routines the DAEObject has to be set up using NonlinearSetup. This function returns a DAEObject containing additional information which is automatically used later on by the simplification functions. Furthermore, NonlinearSetup performs the numerical reference simulations which are used for error calculation. Besides the input and output variables you have to specify which analysis modes to consider during subsequent simplifications.

The DAEObject dae has to be a DC or Transient DAEObject. The argument inputs is a symbol or a list of symbols denoting the input parameters to be swept. In this context input parameters are parameters of the DAEObject (not variables). Use GetParameters to obtain a list of valid parameters. Further, outputs is a symbol or a list of symbols denoting the output variables which are used for error control. In this context output variables are variables of the DAEObject (not parameters). Use GetVariables to obtain a list of valid variables.

The rules -> {} specify the analysis modes to be used during error control and some mode-specific settings for the simplification routines. Here, can be DT (DC-transfer analysis) or AC. If the AC analysis is chosen, DT settings have to be specified, too. The mode settings are given by a sequence of rules. The format is described below.

Additionally, NonlinearSetup provides the following option:

Options for NonlinearSetup.

You can use NonlinearSettings to inspect the settings of the nonlinear simplifications currently stored in a DAEObject. Use GetDAEOptions[dae, NonlinearOptions] to get a list of all nonlinear simplification settings stored in the DAEObject.

See also: GetVariables, GetParameters, NonlinearSettings, Section 3.7.2.

DT mode specifications

Settings for DT mode.

The range in which to sweep the input parameters during simplification is specified by the paramsweep value of the Range option. The range specification has to be given in the standard format for Analog Insydes parameter sweeps which is described in Section 3.7.2. Note that you have to specify a range for each input parameter.

SimulationFunction, ErrorFunction, and MaxError are optional, whereas Range is a required argument.

If no SimulationFunction option is specified, the default function is used. The default DT simulation function DefaultDTSimulation calls NDAESolve to calculate the DC operating points. DefaultDTSimulation inherits almost all options from NDAESolve. The following options have a special meaning when used with DefaultDTSimulation:

Options for DefaultDTSimulation.

Besides the default simulation function you can define your own DT simulation function and specify it as SimulationFunction in the DT mode settings for NonlinearSetup. During the setup and the nonlinear simplifications this function will be called with the following arguments:

Pattern for a user-defined DT simulation function.

Here, dae is a DC or Transient DAEObject, refsim is the list of numerical reference values and opts are additional options.

The simulation function must return the DC operating points in the same format as NDAESolve returns DC operating points of a parameter sweep (see Section 3.7.2).

Similarly, you can define your own DT error function instead of the default error function and specify it as ErrorFunction in the DT mode settings for NonlinearSetup. During the simplification routines this function is used to calculate the error with the following arguments:

Pattern for a user-defined DT error function.

Here, newval and oldval are the numerical solutions of the simplified and the original DAE system, outputsymbols is a list of all output symbols.

The error function must return a list of rules { -> , }, which specifies the numerical error for each output symbol. The default DT error function calculates the maximum absolute error.

An example for a user-defined simulation and error function and of the corresponding call to NonlinearSetup is given in the example section below.

Instead of specifying the maximum allowed error for output variables for each call to the nonlinear simplifications routines separately, you can specify global maximum errors for output variables using the MaxError argument. These values are used if no error value is given in the call to the nonlinear simplification routine. The value of this argument has to be a list of rules of the form outvar -> error.

AC mode specifications

Settings for AC mode.

SimulationFunction, ErrorFunction, and MaxError are optional, whereas Range is a required argument.

If you specifiy AC settings you have to specify DT settings, too. The parameter sweep settings paramsweep must be a subset of the parameter sweep given in the DT settings.

The default AC simulation function is called DefaultACSimulation. This function calls ACAnalysis to perform the numerical calculation. DefaultACSimulation inherits almost all options from ACAnalysis.

Besides the default simulation function you can define your own AC simulation function and specify it as SimulationFunction in the AC mode settings for NonlinearSetup. During the setup and the nonlinear simplifications this function will be called with the following arguments:

Pattern for a user-defined AC simulation function.

Here, dae is a Transient DAEObject, refsim is the list of numerical reference values and opts are additional options.

The simulation function must return a list of the AC solutions in the same format as ACAnalysis returns the result (with the option setting InterpolateResult -> False).

Similarly, you can define your own AC error function instead of the default error function and specify it as ErrorFunction in the AC mode settings for NonlinearSetup. During the simplification routines this function is used to calculate the error with the following arguments:

Pattern for a user-defined AC error function.

Here, newval and oldval are the numerical solutions of the simplified and the original dae system, outputsymbols is a list of all output symbols.

The error function must return a list of rules { -> , } which specifies the numerical error for each output symbol. The default AC error function calculates the maximum relative error.

Instead of specifying the maximum allowed error for output variables for each call to the nonlinear simplifications routines separately, you can specify global maximum errors for output variables using the MaxError argument. These values are used if no error value is given in the call to the nonlinear simplification routine. The value of this argument has to be a list of rules of the form outvar -> error.

Examples

Load Analog Insydes.

In[1]:= <<AnalogInsydes`

Read PSpice netlist.

In[2]:= net = ReadNetlist["AnalogInsydes/DemoFiles/Sqrt.cir",
Simulator -> "PSpice"]

Out[2]=

Set up DAE system.

In[3]:= dae = CircuitEquations[net,
AnalysisMode -> DC, ElementValues -> Symbolic]

Out[3]=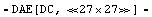

Get all valid symbols that can be used as inputs for NonlinearSetup.

In[4]:= GetParameters[dae]

Out[4]=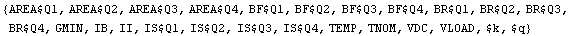

Get all valid symbols that can be used as outputs for NonlinearSetup.

In[5]:= GetVariables[dae]

Out[5]=

In the following we choose VLOAD and II as inputs and V$5 and I$VLOAD as outputs, treating dae as a multi-input/multi-output system. We want to control the DC behavior sweeping VLOAD between and  and II between and  on a uniform two-dimensional grid with  points. The following call to NonlinearSetup prepares a DAEObject with these settings.

Specify settings for nonlinear simplifications.

In[6]:= step1=NonlinearSetup[dae, {VLOAD, II}, {V$5, I$VLOAD},
DT -> {Range ->
{{VLOAD, 0, 3, 1}, {II, 0, 0.003, 0.001}} }]

Out[6]=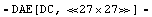

Display settings stored in step1.

In[7]:= NonlinearSettings[step1]

The following code illustrates how to define your own simulation and error function and how to call NonlinearSetup such that these functions are used during nonlinear simplifications.

Define a DT simulation function.

In[8]:= MyDTSimulationFct[dae_, refsim_List:{}, opts___] :=
Block[
{nonlinopts, indepvar, inittime},

{indepvar, inittime, nonlinopts} = GetDAEOptions[
dae,
{IndependentVariable, InitialTime, NonlinearOptions}
];
NDAESolve[
dae,
{indepvar, inittime},
Range /. (DT /. nonlinopts),
opts
]
]

Define a DT error function.

In[9]:= MyDTErrorFct[newval_, oldval_, outputsymbols_] :=
Map[
Rule[#, Max[Abs[(# /. newval) - (# /. oldval)]]] &,
outputsymbols
]

Set up nonlinear simplifications using new simulation and error function.

In[10]:= step1 = NonlinearSetup[dae, {VLOAD, II}, {V$5, I$VLOAD},
DT -> {
Range -> {{VLOAD, 0, 3, 1}, {II, 0, 0.003, 0.001}},
SimulationFunction -> MyDTSimulationFct,
ErrorFunction -> MyDTErrorFct
}
]

Out[10]=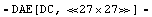

Display settings stored in step1.

In[11]:= NonlinearSettings[step1]