2.2.3 A Brief Preview on Circuit Analysis

There is much more to learn about netlists, but before going into the details let's get an impression of Analog Insydes' basic symbolic circuit analysis functionality. Computing voltages and currents in a circuit requires essentially two steps: Setting up a system of circuit equations and then solving these equations. Circuit equations can be set up automatically by applying the function CircuitEquations to a netlist description.

We set up equations for the voltage divider circuit defined in Section 2.2.1 (see Figure 2.1):

In[9]:= vdeqs = CircuitEquations[voltageDivider]

Out[9]=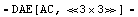

By default, CircuitEquations sets up a system of modified nodal, or MNA, equations (Modified Nodal Analysis) in the frequency domain. The return value is a DAEObject which contains the three components of the linear matrix equation 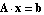, where A is the coefficient matrix, x the vector of unknown voltages and currents, and b the vector of independent sources. To display the system of equations in a more readable form we can apply the command DisplayForm to the DAEObject vdeqs:

In[10]:= DisplayForm[vdeqs]

Out[10]//DisplayForm=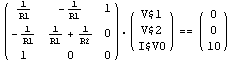

Here, the vector of unknowns comprises the node voltages V$1 and V$2 at nodes 1 and 2, plus the current I$V0 flowing through the voltage source V0.

We can solve the MNA equations by using the function Solve. Given the system of equations and no additional arguments, Solve solves for all voltages and currents listed in the vector of unknowns.

In[11]:= Solve[vdeqs]

Out[11]=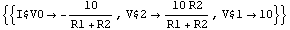

The values of V$1 and V$2 correspond to what we would expect from a voltage divider. If you wonder about the negative sign of I$V0 remember what has been said about positive reference directions of branch voltages and currents in Section 2.2.1.

As a second example we will compute the node voltage at node 2 of the CCCS circuit (see Figure 2.7) as a symbolic function of the circuit parameters in the frequency domain.

In[12]:= cccseqs = CircuitEquations[cccsCircuit];
DisplayForm[cccseqs]

Out[13]//DisplayForm=

The last variable in the vector of unknowns, IC$CC1, denotes the controlling current of the controlled source CC1 (see Section 2.4.1). We can solve for V$2 by explicitly passing this variable as a second argument to Solve.

In[13]:= Solve[cccseqs, V$2]

Out[14]=

The result represents the Laplace transform of the zero-state response of the voltage at node 2, expressed in terms of the complex frequency variable s.

The zero-state response is the response of a system which was in the zero state at the time just prior to the application of the input signal. Zero state means that all initial conditions, i.e. capacitor voltages and inductor currents, are zero.