|
2.2.4 More about Netlists
The General Value-Field Format
As indicated in the previous section, some aspects regarding the netlist format have not yet been mentioned. So far, we have used only the simplest form of writing netlist entries (see Section 2.2.1). In general, however, the value field of a netlist entry does not need to be a single Mathematica expression but may also be a nonempty sequence of options. Netlist entries may thus look like this:
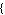 name, name,  nodes nodes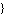 , ,  -> -> 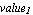 , , 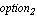 -> -> 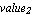 , , 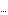 
There are several value-field option keywords which Analog Insydes understands (see Section 3.1.4): Value, Symbolic, Type, Pattern, InitialCondition, Model, and Subcircuit. Their meanings will be discussed in the following subsections.
Value
If the value field is written in its general sequence-of-options form then all of its components must be options. This necessitates an option which specifies the value of the circuit element, namely Value (see Section 3.1.4). With the Value option we can rewrite a netlist entry such as
{R1, {1, 2}, R1}
in the following semantically equivalent general form:
{R1, {1, 2}, Value -> R1}
Of course, as long as the value field contains no more information than only the element value the simple form is the preferred form. Note that if the value field is written in option form, then the Value option must be present.
Symbolic
The Symbolic option (see Section 3.1.4) is closely related to the Value option. It allows you to specify an alternative symbolic element value in addition to a numerical value given as argument to the Value option, for instance:
{R1, {1, 2}, Value -> 100, Symbolic -> R1}
By default, circuit equations are set up using the arguments of the Value options as element values, but CircuitEquations can be instructed to use the symbolic values instead wherever the Symbolic option is given. This allows for assigning both a numerical as well as a symbolic value to a circuit element. You will be able to assess the value of this feature better once you have learned more about the topics described in Chapter 2.3 and Chapter 2.8.
Type
The value field option Type (see Section 3.1.4) allows you to specify the type of an element explicitly, thus overriding the automatic type detection from an element's reference designator. The argument to the Type option must be the full name of a circuit element type supported by Analog Insydes (see Chapter 4.2). The available types are listed in the global variable ElementTypes. Using the Type option we could write a netlist entry for a resistor in the following way even though the name Shunt does not begin with the type tag R.
{Shunt, {1, 2}, Type -> Resistor, Value -> R1}
Moreover, as Analog Insydes generates voltage and current identifiers (see Section 2.4.1) by adding the prefixes "V$" and "I$" to the reference designators, the Type option gives us some more influence on the names of voltages and currents. In this example, the resistor current would be named I$Shunt, whereas it would be named I$R1 for the netlist entries from the previous two subsections.
The example below shows a more convincing application of the Type option. Assume that you have an amplifier circuit with an output load connected between nodes out and ground, and that you wish to calculate the amplifier's frequency responses for both resistive and capacitive loads. You could, of course, write two separate netlists for this purpose. On the other hand, the Type option offers you the alternative to set up only one single netlist but with a variable load type:
amplifier =
Netlist[
{Load, {out, 0}, Type -> loadtype, Value -> loadval},
]
Then, by replacing the type variable with a concrete type name, you can set up circuit equations for a particular type of load, e.g. for a capacitor:
CircuitEquations[
amplifier /. {loadtype -> Capacitor, loadval -> CL}]
Note that in both cases the identifier for the load current will be I$Load, regardless of the load element type eventually selected.
Finally, the Type option helps us to correct a frequently made mistake, which usually occurs when a netlist contains a supply voltage source named VCC. If we relied on automatic type detection from the reference designator VCC, Analog Insydes would give us the error message "Netlist::numnode: Expected 4 nodes but received 2 for VCCSource VCC". The reason for this error is that VC is the type tag for voltage-controlled current sources, so Analog Insydes interprets VCC as (VC)C and not as a voltage source V(CC). This problem can be easily solved by means of the Type directive:
{VCC, {1, 0}, Type -> VoltageSource, Value -> VCC}
Pattern
The Pattern option (see Section 3.1.4) can be used only in conjunction with two-terminal immittances, i.e. impedance and admittance elements such as resistors (Section 4.2.1), conductances (Section 4.2.2), capacitors (Section 4.2.5), and inductors (Section 4.2.6). With this directive you can explicitly choose whether the contribution of an immittance element to a system of modified nodal equations is entered into the matrix using the fill-in pattern for admittances or the pattern for impedances. The two associated values of the Pattern option are Impedance and Admittance.
When setting up modified nodal equations, Analog Insydes automatically converts impedance elements such as resistors into their admittance equivalents in order to keep the matrix size as small as possible. In other words, a resistor with the value R will be treated as an admittance with the value 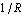 and will be entered into the modified nodal matrix using the fill-in pattern for admittances (see the example in Section 2.2.3). However, if we are interested in computing the current through a particular resistor it would be better to use the fill-in pattern for impedances as this would augment the MNA system by the corresponding branch current. So if we want to calculate the load current of the above-mentioned amplifier using the MNA formulation we would have to select the impedance pattern for the load resistor in order to introduce the branch current I$Load: and will be entered into the modified nodal matrix using the fill-in pattern for admittances (see the example in Section 2.2.3). However, if we are interested in computing the current through a particular resistor it would be better to use the fill-in pattern for impedances as this would augment the MNA system by the corresponding branch current. So if we want to calculate the load current of the above-mentioned amplifier using the MNA formulation we would have to select the impedance pattern for the load resistor in order to introduce the branch current I$Load:
{Load, {out, 0}, Type -> Resistor, Value -> RL,
Pattern -> Impedance}
Let's experiment with some value-field options using the CCCS circuit from Section 2.2.2 (see Figure 2.7). We replace the resistor RL by a variable load type and select the fill-in pattern for impedances.
In[14]:= cccsCircuit2 =
Netlist[
{V0, {1, 0}, V0},
{RB, {1, 3}, RB},
{CM, {1, 2}, CM},
{CC1, {3, 0, 2, 0}, beta},
{Load, {2, 0}, Type -> loadtype, Value -> loadval,
Pattern -> Impedance}
]
Out[15]= 
We choose a resistive load with the symbolic value RL and set up the MNA equations. Due to the Pattern directive, the load current I$Load now appears as an additional variable for which we can solve directly.
In[15]:= cccseqs2 = CircuitEquations[
cccsCircuit2 /. {loadtype -> Resistor, loadval -> RL}];
DisplayForm[cccseqs2]
Out[17]//DisplayForm= 
In[16]:= Solve[cccseqs2, I$Load]
Out[18]= 
Next, we select a capacitive load CL and solve for the load current again.
In[17]:= cccseqs3 = CircuitEquations[
cccsCircuit2 /. {loadtype -> Capacitor, loadval -> CL}];
DisplayForm[cccseqs3]
Out[20]//DisplayForm= 
In[18]:= Solve[cccseqs3, I$Load]
Out[21]= 
InitialCondition
With the InitialCondition option (see Section 3.1.4), you can specify initial currents and voltages for the dynamic elements Inductor and Capacitor, respectively. If no initial condition is given explicitly, it will be assumed to be zero (AC analysis) or will be calculated automatically from the operating-point data (transient analysis).
As an example, we set an initial capacitor voltage of V0 for the netlist entry C1 of the following filter circuit:
In[19]:= filter =
Netlist[
{V1, {1, 0}, V1},
{R1, {1, 2}, R1},
{C1, {2, 0}, Value -> C1, InitialCondition -> V0}
]
Out[22]= 
In[20]:= filtereqs = CircuitEquations[filter,
InitialConditions -> Automatic];
DisplayForm[filtereqs]
Out[24]//DisplayForm= 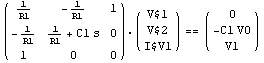
See Section 2.7.5 for a description of initial condition handling during equation setup.
Model, Subcircuit
The purpose of the Model and Subcircuit directives is to mark a netlist entry as being a reference to a device model or subcircuit definition. Chapter 2.3 deals with the details.
|