Acceleration
2D/3D• Acceleration[point] returns the global acceleration vector, {ddX, ddY} (2D) or {ddX, ddY, ddZ} (3D) of the specified point.
• Acceleration[bnum, lpnt] is interpreted as Acceleration[Point[bnum, lpnt]].
• Acceleration[bnum] returns the acceleration and angular acceleration coordinates of body bnum in a flat list.
• The bnum argument can take any of the forms accepted by Loads to obtain the acceleration coordinates of multiple bodies.
• Acceleration is also a setting for the Solution option for several Mech functions.
• Solution->Acceleration causes such functions to seek a solution for the location, velocity, and acceleration of the current model. • Acceleration[All] returns the entire vector of acceleration coordinates.
• The behavior of Acceleration[bnum] varies depending on whether the current solution method is Angular or Euler.
• To use Acceleration[bnum], bnum must be the number of a body in the current model.
• In Modeler2D with the Euler solution method, Acceleration[2] returns {X2dd, Y2dd, Ei2dd, Ej2dd}, but with the Angular solution method, Acceleration[2] returns {X2dd, Y2dd,  2dd}. 2dd}.
• In Modeler3D with the Euler solution method, Acceleration[2] returns {X2dd, Y2dd, Z2dd, Eo2dd, Ei2dd, Ej2dd, Ek2dd}, but with the Angular solution method, Acceleration[2] returns {X2dd, Y2dd, Z2dd, 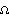 x2d, x2d, 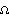 y2d, y2d, 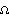 z2d}. z2d}.
• Acceleration[sym] or Acceleration[{sym, ... }] returns the acceleration coordinates associated with the specified location coordinates sym.
• The alternatives to the Acceleration setting for the Solution option are Location, Velocity, Static, Kinematic, and Dynamic.
• See also: Alpha, SolveMech, SetCouple. Further Examples Load the Modeler2D package and define a simple model. Here is an expression representing the acceleration vector of a point at {3, 0} on the crank.
Out[2]= | 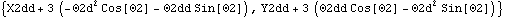 |
Here are the variables used to represent the linear and angular acceleration of the crank and link bodies.
Out[3]= | 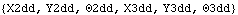 |
Here is a solution to the current model with velocity and acceleration terms included.
Out[4]= |  |
Here is the numerical value of the acceleration of a point at {3, 0} on the crank.
Out[5]= | 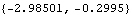 |
See HelpModel2D.
|