The state-feedback full-rank algorithm described in Patel and Munro (1982) is based on the Luenberger controllable canonical form of the system, which is described in Section 6.4. Under this transformation, the resulting matrices 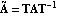 and and 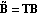 have special block-structured forms. have special block-structured forms. Using this algorithm, the state-feedback matrix K that places the poles of a multi-input system 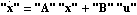 at at  {1}, {1}, {2},..., {2},..., n can be found as n can be found as where Q is a p × p nonsingular matrix formed from the nonzero rows of  , and , and 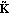 is the full-rank state-feedback matrix determined in the new basis such that is the full-rank state-feedback matrix determined in the new basis such that 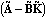 becomes block triangular, or block diagonal, with each diagonal block containing part of the desired closed-loop system characteristic polynomial. becomes block triangular, or block diagonal, with each diagonal block containing part of the desired closed-loop system characteristic polynomial. The advantage of this algorithm over the dyadic algorithms, such as Ackermann's (Control System Professional, Section 9.1.1), Munro's spectral algorithm (Section 6.2), and Young and Willems mapping algorithm (Section 6.1), is that it uses all the system inputs to determine the desired full-rank state-feedback matrix, and this usually results in much lower gain values being applied to the system state variables. The function StateFeedbackGains with the option Method  FullRank implements this algorithm. FullRank implements this algorithm. Method  FullRank FullRank | compute the state-feedback matrix using the full-rank algorithm |
State-feedback design using the full-rank algorithm. Make sure the application is loaded. Consider again the state-space model of the aircraft. | Out[3]= | 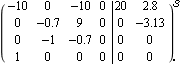 |
Here are the desired closed-loop system poles. This finds the full-rank state-feedback compensator. | Out[6]= | 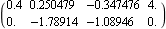 |
This is the infinity norm of the resulting state-feedback matrix. | Out[8]= | 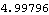 |
The norm is much lower than the one obtained with the mapping or spectral methods. As a discrete-time example, consider the locally linearized model of the mixing tank system described in Section 10.1 of Control System Professional. This is the state-space continuous system realization of the mixing tank system. | Out[10]= | 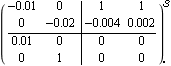 |
This is a discrete-time approximation to the system sampled with a period of 5 seconds. | Out[12]= | 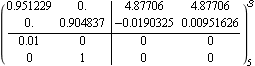 |
These are its open-loop eigenvalues. | Out[14]= | 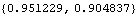 |
In Section 6.1 of Control System Professional, an optimal state-feedback controller was designed, as follows. This assigns some values to the weighting matrices Q and R. | Out[16]= | 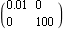 |
| Out[18]= | 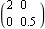 |
This finds the optimal gain matrix. | Out[20]= | 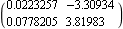 |
This is the resulting closed-loop system. | Out[22]= | 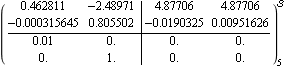 |
These are the closed-loop system poles. | Out[24]= | 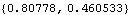 |
This is the infinity norm of the resulting state-feedback matrix. | Out[26]= | 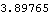 |
Now, consider the state-feedback gains needed to achieve the same closed-loop poles, using pole assignment. This finds the state-feedback compensator using the mapping algorithm. | Out[28]= | 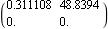 |
Since row 2 of the compensator is zero, the best input determined using the condition number of the resulting controllability matrix, is input 1. This is the infinity norm of the resulting state-feedback matrix. | Out[30]= | 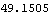 |
This finds the state-feedback compensator using the full-rank algorithm. | Out[32]= | 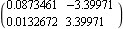 |
This is the infinity norm of the resulting state-feedback matrix. | Out[34]= | 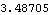 |
The infinity norm of the resulting state-feedback matrix obtained using the full-rank pole assignment algorithm is similar to that obtained using optimal control, since both approaches use all the system inputs. However, the result obtained using the mapping algorithm for pole assignment produces a much larger infinity norm. |