FRatioCI[ratio,n,m]
gives a confidence interval based on an F-ratio distribution with n and m degrees of freedom.


FRatioCI
FRatioCI[ratio,n,m]
gives a confidence interval based on an F-ratio distribution with n and m degrees of freedom.
Details and Options
- To use FRatioCI, you first need to load the Hypothesis Testing Package using Needs["HypothesisTesting`"].
- FRatioCI[ratio,n,m] gives a confidence interval {min,max} for a ratio of variances estimated by ratio.
- For confidence level
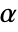 ,
, 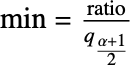 and
and 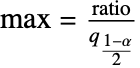 where
where 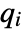 is the
is the 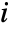
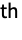 quantile of an F-ratio distribution with n numerator and m denominator degrees of freedom.
quantile of an F-ratio distribution with n numerator and m denominator degrees of freedom. - FRatioCI is the confidence interval for a ratio of population variances based on sample variances estimated from samples of size
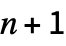 and
and 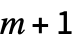 .
. - The following option can be given:
-
ConfidenceLevel 0.95 probability associated with a confidence interval
Tech Notes
Related Guides
Text
Wolfram Research (2007), FRatioCI, Wolfram Language function, https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioCI.html.
CMS
Wolfram Language. 2007. "FRatioCI." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioCI.html.
APA
Wolfram Language. (2007). FRatioCI. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioCI.html
BibTeX
@misc{reference.wolfram_2025_fratioci, author="Wolfram Research", title="{FRatioCI}", year="2007", howpublished="\url{https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioCI.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_fratioci, organization={Wolfram Research}, title={FRatioCI}, year={2007}, url={https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioCI.html}, note=[Accessed: 03-March-2026]}