WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

FRatioPValue[x,n,m]

自由度が n と m のF分布において x を超える累積確率を返す．

詳細とオプション
Details and Options Details and Options
例題  
例  
オプション  
TwoSided  
関連項目
テクニカルノート
関連するガイド
引用書式
HypothesisTesting`
HypothesisTesting`

FRatioPValue

FRatioPValue[x,n,m]

自由度が n と m のF分布において x を超える累積確率を返す．

詳細とオプション

  • FRatioPValueを使うためには，まず仮説検定パッケージをロードしなくてはならない．それにはNeeds["HypothesisTesting`"]を実行する必要がある．
  • x が自由度 n および m のF分布の中央値より小さい場合，片側 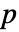値はCDF[FRatioDistribution[n,m],x]であり，それ以外の場合は1-CDF[FRatioDistribution[n,m],x]である．
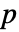  • 両側 値は片側 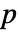値の2倍である．
  • 次のオプションを使うことができる：
  • TwoSided False両側検定を行うかどうか

例題

すべて開く すべて閉じる

例  (1)

自由度2および5のF分布における10の p 値：

オプション  (1)

TwoSided  (1)

両側 p 値：

Wolfram Research (2007), FRatioPValue, Wolfram言語関数， https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html.

テキスト

Wolfram Research (2007), FRatioPValue, Wolfram言語関数， https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html.

CMS

Wolfram Language. 2007. "FRatioPValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html.

APA

Wolfram Language. (2007). FRatioPValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html

BibTeX

@misc{reference.wolfram_2025_fratiopvalue, author="Wolfram Research", title="{FRatioPValue}", year="2007", howpublished="\url{https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html}", note=[Accessed: 27-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_fratiopvalue, organization={Wolfram Research}, title={FRatioPValue}, year={2007}, url={https://reference.wolfram.com/language/HypothesisTesting/ref/FRatioPValue.html}, note=[Accessed: 27-October-2025]}