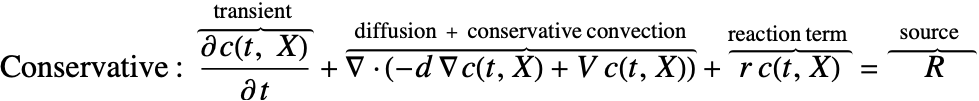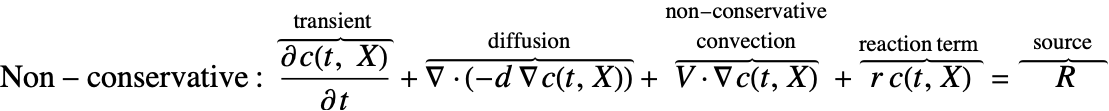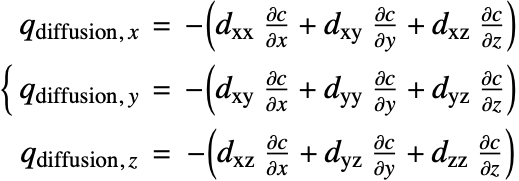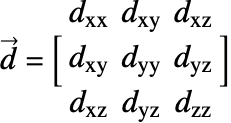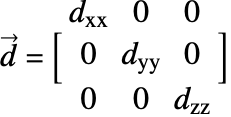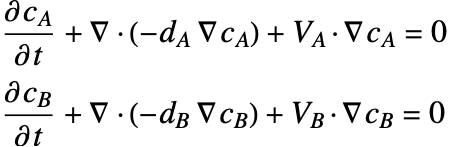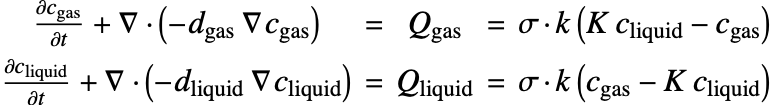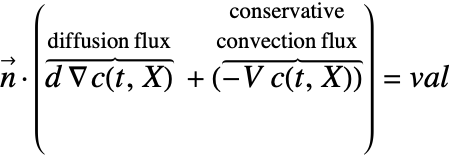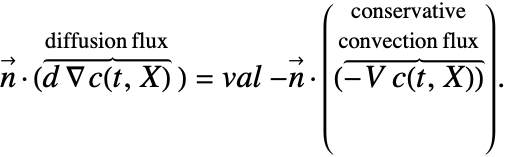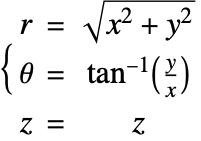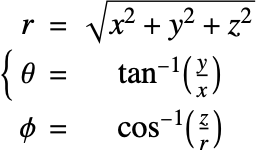Mass Transport
| Introduction | Appendix |
| Mass Balance Equation | Nomenclature |
| Boundary Conditions in Mass Transport | References |
Introduction
This tutorial gives an introduction to modeling mass transport of diluted species. Equations and boundary conditions that are relevant for performing mass transport analysis are derived and explained.
Mass transport is a discipline of chemical engineering that is concerned with the movement of chemical species. The two mechanisms of mass transport are mass diffusion and mass convection. The driving force behind a mass diffusion is the difference in a species concentration at different locations. Mass convection, on the other hand, only occurs when species are transported in a moving fluid medium. The combination of these two mechanisms leads to changes in the species concentration field over time and is modeled with a mass balance equation.
The modeling process results in a partial differential equation (PDE) that can be solved with NDSolve. Furthermore, in this tutorial different types of mass transport boundary conditions are introduced. For the boundary conditions given we show how to model various real world chemical species interactions.
This notebook provides an introduction overview of how to model mass transport. The focus is to present simple yet illustrative examples. Extended examples that show industrial applications of mass transport modeling can be found in the Mass Transfer Model Collection.
Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high quality graphics remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Mass Balance Equation
In the following sections we will start with an introduction of the mass balance equation, followed by a derivation of the equation and examples of how it is mapped to the Wolfram language.
Mass Balance Equation Introduction
There are two different formulations that can be used to model the transport of chemical species through mass diffusion and mass convection. These are the conservative and non-conservative forms of the mass balance equation:
The dependent variable in the mass balance equation is the species concentration 
, which varies with time 
and position 
. The partial differential equation (PDE) model describes how chemical species are transported over time in a solid or fluid medium.
Typically, the non-conservative formulation is appropriate for incompressible fluids where the concentration field 
is expected to be smooth. The derivation in the section Mass Balance Equation Derivation will help explain why this is the case.
Beside the time derivative part both PDEs are made up of several components. First and foremost there is a diffusive term: 
with a diffusion coefficient 
, which is also known as the species diffusivity. In some cases the diffusion coefficient may depend on other properties such as a temperature 
and the concentration 
itself making the equation nonlinear. The details of variable diffusion coefficients will be discussed later in the section: Variable Mass Diffusion Coefficient.
The second component is a convective term. In the conservative formulation the convective term is 
. In the non-conservative formulation the convective term is 
. The difference between the conservative and the non-conservative form are explained in the section Mass Balance Equation Derivation. In either case, this term is only present if mass transport occurs in a fluid medium with a fluid flow velocity 
. If the simulation medium is a solid then this term is zero, regardless of which formulation is made use of.
Contrary to the convective term, the diffusive term may be present if the medium is solid or fluidic.
The term 
denotes a mass production or consumption rate of chemical species, typically due to a chemical reaction. This will be further explained in the Mass Transport with Chemical Reaction section.
Mass Balance Equation Derivation
To derive the mass balance equation we start from the law of mass conservation. In a system the total mass change must equal to net mass formation minus the net mass outflow flow. A mass balance can then be expressed as:
To formulate the mass balance equation the mass of a chemical species is balanced within a unit volume domain 
. The mass balance is based on the concentration 
of the species, which denotes the amount of species per unit volume measured in moles. The molar concentration 
could be converted to a mass concentration 
by:
where 
is the amount of the species in moles, 
is the volume of the domain, 
is the mass of the species and 
is the molar mass, which is the mass per unit mole of the species.
In the above graphics, 
is the concentration and 
is the area of the domain. The total mass within the control area is then equal to 
. The term 
denotes the net rate of mass formation due to chemical reactions inside the domain 
. The net mass flux 
represents the net rate of mass flow that exits through the boundaries.
The above consideration in 2D is valid in any dimension, for example, in a 3D domain the concentration 
is given in 
and the volume in 
.
The unit of the mass flux 
through the boundary depends on the dimensionality of the boundary. In a 3D domain the boundary is represented by 2D surfaces, and the mass flux 
has a unit of 
. In a 2D domain, however, the boundary is made up from 1D lines, which makes the unit of 
become 
. In 1D the boundary is represented by a dimensionless point and the heat flux 
has a unit of 
.
The mass conservation within the domain 
can be described by the following equation:
That is, the rate of the mass change 
is equal to the net rate of mass formation 
inside the domain minus the net mass flux 
that exits the domain.
Here the mass flux 
can be divided into two parts: a diffusive mass flux 
and a convection mass flux 
. The diffusion flux describes the mass transport due to a concentration gradient in the mass species concentration, and is proportional to its diffusivity 
:
Equation (1) is also known as Fick's law of diffusion [2]. The minus sign states that the mass diffusion is in the direction of decreasing concentration.
The convection flux denotes the mass transported by a flow of the medium, and is proportional to the flow velocity 
:
If the mass transport occurs in a solid medium, then, because a solid can not have an internal velocity field 
by definition, the convection term is set to 
.
Inserting (3) and (4) into the mass conservation equation (5) yields the conservative mass transport model.
When expressing (6) in the coefficient form of PDEs: 
, one has to be careful about the sign of the convection term 
.
Equation (7) is known as the conservative mass balance equation since the convective mass flux term, 
, and with it the flow velocity 
is inside of the divergence operator.
To obtain the non-conservative formulation equation (8) is expanded using the chain rule:
This results in the terms 
and 
. For an incompressible fluid the divergence of the flow velocity is zero (
) by definition and thus the term 
equals to zero, resulting in the non-conservative mass balance equation (9).
If possible, it is recommended to use the non-conservative form for incompressible fluids when solving mass transport models. The two main reasons are:
- The removal of the term
ensures that the incompressible flow field 
will not induce any nonphysical mass production or consumption into the source term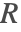 
.
- The mass convection term (10) is outside of the divergence operator, which prevents the growth of spurious oscillation of the solution field [11] and makes the PDE model more stable and efficient to solve.
However, the non-conservative formulation is only applicable for incompressible fluids where the concentration field 
is expected to be smooth. For mass transport in a compressible medium the conservative formulation (12) should be used instead. Note that when the fluid flow velocity is zero both models simplify to the same PDE.
In this tutorial we will be focus on incompressible fluid media, and the non-conservative mass balance equation (13) will be used as the default PDE setup for the mass transport model. However, in the later section Boundary Conditions in Mass Transport we will present the boundary condition setup for both the conservative and the non-conservative formulation.
The mass balance equation may also be expressed in cylindrical and spherical coordinates. The details can be found in the appendix section Special Cases of the Mass Balance Equation.
In the next section we will set up the mass transport model function in the Wolfram language.
Mass Transport Model Setup
The inputs needed for a mass transport model in Cartesian coordinates are
 | the concentration variable | |
 | the spatial independent variables | |
 | a velocity field | |
 | the species diffusivity | |
 | the reaction rate (also known as the rate of mass formation) |
Note that this model definition uses inactive PDE operators. The tutorial Numerical Solution of Partial Differential Equations has several sections that explain the use of inactive operators.
In the next few sections the mass transport model will be discussed in more details. We will present various types of the usage of the mass transport PDE with examples.
Initial Mass Transport Example
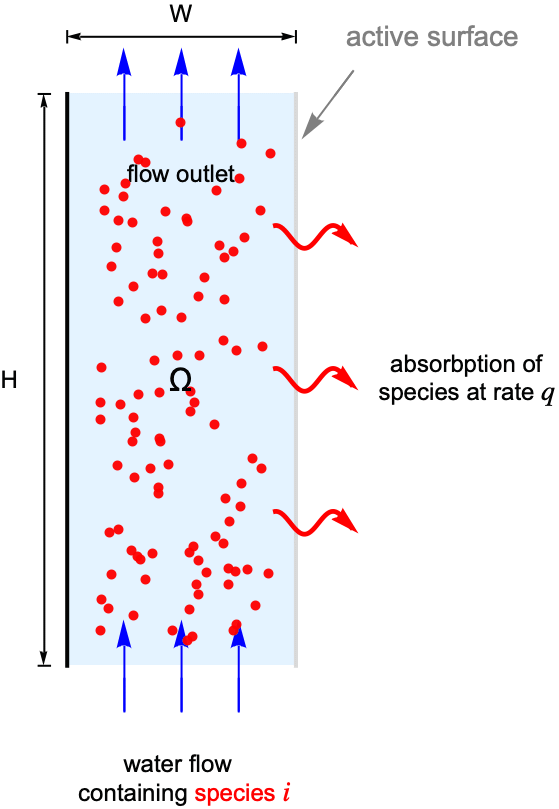
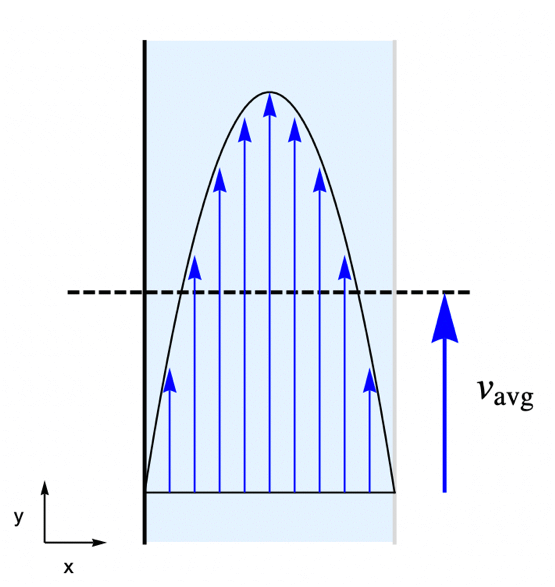
The purpose of the 2D stationary example below is to demonstrate a typical workflow of mass transport modeling.
For this consider a parallel-plate reactor with a species 
solved in water. As the water flow passes through the reactor part of the species 
will be absorbed by the active surface located at the right side. Our goal is to find the steady-state concentration field for the species 
within the reactor.
To make the example concrete we use a width of 
and a height of 
for the model domain 
, and set the absorption rate 
on the active surface at the right shown in light gray. The left side wall shown in black is assumed to be impermeable by the species 
and thus has no mass flux across it.
For this example we use an arbitrary mass diffusion coefficient.
In this example the water is flowing through the reactor at an average velocity of 
. The flow velocity field 
within the reactor is determined by the laminar profile:
Next, the boundary conditions at each boundary are set up. The details of the setting up mass transfer boundary conditions will be explained in detail in the section Boundary Conditions in Mass Transport.
At the flow inlet the species concentration is held fixed at 
as if there is an infinite supply of the species 
below the inlet.
On the active surface the species 
is continuously absorbed at a given rate of 
. This is modeled by a mass flux boundary condition.
Since the left side wall is impermeable by the species 
, an impermeable boundary condition is used to model the boundary where there is no mass flux across it.
A default outflow boundary condition is implicitly applied at the top boundary to model the flow outlet where the species 
is transported out of the domain.
Next we solve the mass transport PDE model with a prescribe flow field 
and an arbitrarily chosen species diffusivity of 
.
Note that the argument "NoReaction" is used to denote that there is no internal reaction within the domain.
In this example the species 
is exclusively absorbed on the active surface at the right boundary at a rate of 
, resulting in a layer-like concentration field.
Mass Transport with a Chemical Reaction
In the previous section the chemical species did not undergo a chemical reaction. In the following section the modeling of chemical reactions is explained.
The term 
in the mass balance equations (14) and (15) is used to model a mass formation (
) or consumption rate (
) within the domain. A typical phenomena that leads to a mass formation or consumption are chemical reactions. As an example consider the following 2D transient model:
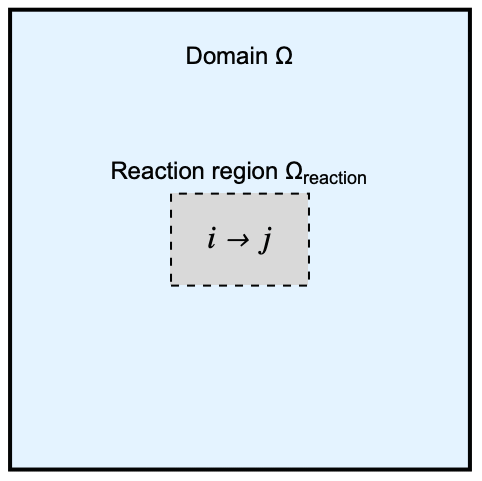
The model domain 
has a internal rectangular region 
where an unimolecular reaction occurs. We speak of unimolecular reactions when a chemical species 
undergoes a self-transformation into a single product 
:
In this example we assume the reaction to be a first-order reaction [16], that is, the mass consumption rate 
of the reactant 
will be linearly proportional to the concentration 
of the reactant itself:
Here 
is the reaction rate constant and has a unit of 
. For most chemical reactions the rate constant 
is temperature-dependent and can be computed by the Arrhenius equation [17]. In this example, however, we choose a constant 
for the sake of simplicity.
Typically applications where the reaction rate 
is temperature dependent are modeled as coupled equations where a heat equation is linked with a mass transport equation. An example of the setup of and the modeling with a temperature-dependent reaction rate 
can be found in the multiphysics application model Thermal Decomposition.
Note, that by using exact numbers for the region the region membership test simplified to an If statement.
To highlight the effect of the chemical reaction, we assume that there is no moving flow within the domain, which means that the mass transport is by diffusion only.
, an initial concentration field 
, and a species diffusivity 
.
See this note about improving the visual quality of the animation.
The species 
has an initial concentration field 
of 
, and is gradually consumed by the reaction within the region 
. The excess species 
outside the region 
then fills in by diffusion due to the concentration gradient, which brings down the overall concentration within the model domain.
Anisotropic and Orthotropic Mass Diffusion
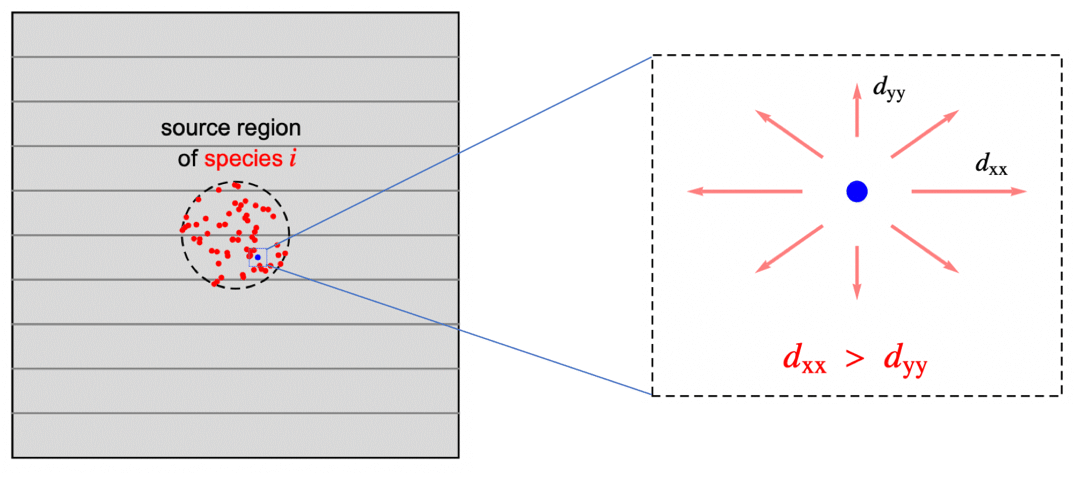
In previous sections the assumption was that the species is transported in an isotropic medium, that is, the rate of the diffusive mass transfer is independent of its direction and given by the same the concentration gradient 
. In reality, however, a medium may be anisotropic. Anisotropic diffusion means that the species diffuses in different directions with a different rate. Orthotropic diffusion is a special case of anisotropic mass diffusion that will be described below. Anisotropic behaviour can be found all the way from natural products to sophisticated composite materials and as such is an important phenomena to be able to model.
Since the species diffusivity 
varies in different directions, the diffusion flux term (18) is then rewritten as:
is the diffusivity tensor. 
and 
are called the principle diffusion coefficients and off-diagonal diffusion coefficients, respectively.
With orthotropic diffusion the species diffusivity of a material is symmetric but distinct along the principle directions 
, 
and 
, such as shown in the graphics below. All the off-diagonal diffusion coefficients are zero. This behaviour can be seen, for example, in fiber composite materials. Then the diffusion tensor becomes:
As an example, consider a 2D composite material with a layered-like structure. The initial concentration of the species can be described by a Gaussian bell shape centered at 
. The species then gradually diffuse throughout the entire domain.
The illustration above depicts the orthotropic case where the species diffuses slower in the vertical direction where it passes across the internal boundaries of the layered structure shown as gray lines. The diffusivity tensor can be described by:
See this note about improving the visual quality of the animation.
The species is transported faster in the horizontal direction, resulting in a higher concentration zone within the band between 
.
Variable Mass Diffusion Coefficient
In the preceding sections the assumption was that the mass diffusion coefficient and hence the species diffusivity is either a constant scalar 
for an isotropic medium or a constant tensor 
for an anisotropic medium. In reality, however, the diffusivity might change significantly with temperature 
and the species concentration 
. We will look at both phenomena in turn.
Temperature Dependence of the Diffusion Coefficient
When modeling mass transport in a medium with a non-uniform temperature field, it is better to account for the temperature dependence of the diffusion coefficient 
. As a starting model the diffusion coefficient can be predicted by Arrhenius' equation:
is the species diffusivity 
,
is the maximum species diffusivity at infinite temperature 
,
is the absolute temperature 
,
is the activation energy for diffusion 
,
is the gas constant 
.
The exponential form of this relation means that the species diffusivity 
can grow quickly with temperature 
.
As an example consider a 1D domain 
with a prescribed temperature field increase from left to right as: 
.
At time 
the species is confined around the center, and can be described by a Gaussian distribution.
At time 
the species is confined around the center, and then gradually diffused throughout the domain. Note that the species diffused faster to the right side due to the higher temperature in that region.
In this example the temperature field 
is prescribed. However, to solve a mass transport model with an unknown temperature field, we have to construct a multiphysics model that couples a heat transfer model with a mass transport model. Such a coupled heat transfer mass transport multiphysics application model is shown in the model collection in the Thermal Decomposition example.
Concentration Dependence of the Diffusion Coefficient
For some mass transport applications such as drug delivery in blood and pollutants emission in air, the transported species may have unique interaction with the molecules of the medium [19, 20]. In such cases the diffusion coefficient 
will be affected by the concentration field 
of the transported species, leading to a nonlinear mass balance equation. The non-conservative nonlinear mass balance equation is given as:
The diffusion coefficient 
in the PDE model is now a function of the concentration 
itself. The expression of the nonlinear diffusion coefficient is usually determined experimentally and depends on the type of transported species and the medium.
As an example, consider a 1D mass transport model with an initial concentration field of 
, a reference diffusion coefficient 
and a concentration-dependent diffusion coefficient 
. In this case the species diffusivity 
will increase with higher concentration 
.
To model the supply of species into the domain, a constant mass flux 
is applied at the left hand boundary.
, an initial concentration field 
and a reference diffusivity 
To better understand the effects of the nonlinearity compare to a linear mass transport PDE.
In both the linear and nonlinear model the species entered the domain from the left with a constant mass flux 
. However, for the non-linear model the diffusion coefficient 
will increase with the concentration 
, which further speeds up the mass transport and results in a flatter concentration field.
Interphase Mass Transfer
In the preceding sections we've considered the mass transfer by mass convection and mass diffusion in a single phase. However, there are many situations in nature where two different phases are in contact, and mass may be transported from one phase to the other. This process in known as interphase mass transfer.
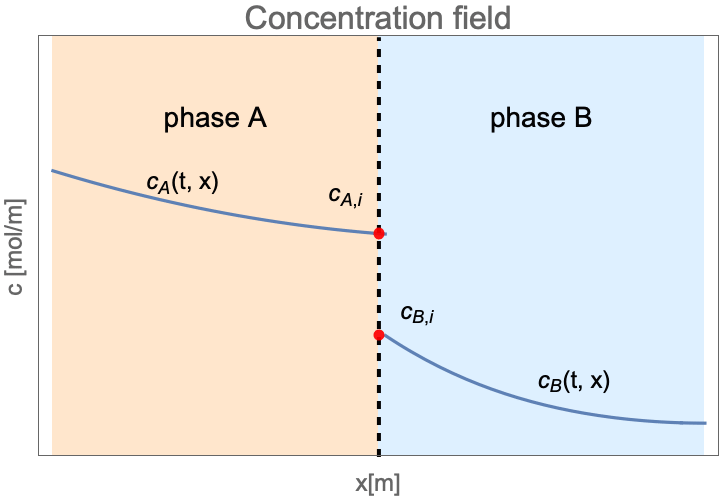
Unlike the single-phase mass transfer where the concentration field is always continuous, the species concentration can jump at the interface between two states as follows:
Here 
and 
are the concentration of species dissolved in phase 
and phase 
. The subscription 
denotes the species concentration at the interface between two phases.
A separate mass balance equation should be used to describe the species concentration 
in phase 
and 
in the phase 
:
At the interface of two phases the concentration may be discontinuous between 
and 
. The ratio 
is known as the equilibrium distribution coefficient 
.
The coefficient 
depends on pressure, temperature and the chemical properties of the transported species and the media of both phases. The value 
can be determined by experimental measurement [21].
Assuming the molecules of species can penetrate quickly through the interface of two phases, the equilibrium condition at the interface (22): 
will be reached instantaneously is satisfied at all times.
This assumption was first proposed by Whitman [23] as the two-resistance theory, and is valid for most cases of the interphase mass transfer. However, in case a chemical reaction occurs at the interface, additional repulsive or attractive forces may act on the transported species and then this assumption will no longer be valid.
Consider a 1D model where sulfur dioxide, 
, is transferred from air 
into water 
. To model the interphase mass transfer we will define a thin interphase region between the two different phases, which will allow us to enforce the equilibrium condition (24) via a coupled fictitious mass sources and handle the discontinuity of the 
concentration at 
.
Here we set the thickness 
of the interphase region to be 
of the length 
of the domain. Note that if 
is set too small a numerical instability may occur around the interface.
Next we define a full element mesh with internal markers to distinguish the gas, liquid and interphase regions. For clearer assignment of markers an association is used.
The diffusion coefficients of 
in the gas and in the liquid phases are given by 
and 
respectively. Note that 
and 
are only valid within the interphase region as well as their own phase.
To model the transfer of 
between two phases we add the coupling mass source terms 
and 
in the governing mass balance equation (25), leading to:
Here 
and 
are set at 
so that the equilibrium condition (26): 
can be enforced at the interface. In the equation 
is the interphase mass transfer coefficient, and 
is a switch that turns on 
within the interphase region and off 
otherwise.
Based on the two-resistance theory mentioned above, the equilibrium at the interface is considered to be reached instantaneously and maintained at all times. This condition can be modeled by setting the mass transfer coefficient 
to be infinitely large.
In practice, we can choose 
to be greater than the species diffusivity 
and 
) by several orders of magnitude.
Note that due to the mass conservation, the coupling source terms 
and 
have the same magnitude but opposite sign.
To model the supply of 
into the domain, a constant mass flux 
is applied at the left hand boundary of the air region.
concentration 
in the gas phase and 
in the liquid phase.To study the effect of the equilibrium coefficient 
on the interphase mass transfer, the PDE model is solved repetitively with ParametricNDSolveValue at 
, 
and 
.
Note that as the equilibrium coefficient 
deviates from 
, the jump between 
and 
increases.
The strategy presented in this section can also be applied in modeling mass transfer across a membrane. In that case, however, an additional repulsive force (i.e. surface resistance) may play a role, and the time for the membrane to reach the equilibrium condition (27) should also be considered. This can be done by selecting a 
value in (28) based on the surface resistance of the membrane.
Mass Source Types
Mass sources like volumetric, layer and point sources can be modeled in a similar fashion as explained in the corresponding Heat Transfer model section.
Boundary Conditions in Mass Transport
The most common boundary conditions in mass transport modeling can be modeled with DirichletCondition, NeumannValue and PeriodicBoundaryCondition, and can be categorized in the following four types:
- Dirichlet type boundary conditions. This type of boundary condition specifies the species concentration
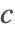at the boundary, and can be modeled with DirichletCondition.
- Neumann type boundary conditions. This type of boundary condition specifies the mass flux
at the boundary, and can be modeled with NeumannValue.
- Robin type boundary conditions. This type of boundary condition specifies the relation between the species concentration
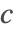and its normal derivatives at the boundary, and can modeled with a NeumannValue since Robin type boundary conditions are technically generalized Neumann boundary conditions.
- Periodic boundary conditions. This type of boundary condition specifies the species concentration
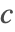at one part of the boundary to be the same at another part, and can be modeled with PeriodicBoundaryCondition.
Under these four types, the following boundary conditions are introduced:
The following section describes several physical boundary conditions common in modeling mass transport and how they can be represented with the use of DirichletCondition, NeumannValue and PeriodicBoundaryCondition. For this purpose the boundary condition currently discussed is always at the left hand side of the example simulation domain. In some examples additional boundary conditions are at the right hand side to better demonstrate the behaviour of the boundary condition at the left hand side.
Note that the setup of Neumann type boundary conditions will be slightly different between the conservative model and non-conservative model. The detail of this difference is presented in the following section.
Neumann Values for Conservative and Non-conservative Models
In a previous section we have presented the derivation and setup of the conservative and non-conservative mass transport model. The difference of the model formulation has an impact on how Neumann type boundary conditions are to be set up and what they mean.
With the conservative formulation the NeumannValue specifies the boundary values for 
. With NeumannValue[val,X∈Γb] we have:
With the non-conservative formulation the NeumannValue specifies the boundary values for 
. With NeumannValue[val,X∈Γb] we have:
Note that for the conservative formulation the term: 
, which is the mass transported by a flow of the medium across the boundary, is also included in the Neumann value.
In some of the boundary conditions presented the form of the Neumann value needs to changed. This means that, for example a Neumann value in the conservative form like eqn (29) will have to be transformed into
Transformations of this sort pose a problem as usually the normal 
in a Neumann formulation like the left side of eqn (30) is never actually computed but replaced with the value of the right hand side of eqn (31). Once a normal 
appears on the right hand side of the equation that value of the normal will have to be computed and this is done automatically. If the boundary unit normal is simple it can be specified with the model parameter "BoundaryUnitNormal". This may increase computational efficiency both in speed and memory usage.
Before the mass transport boundary conditions for both conservative model and non-conservative model are presented some example model parameters are set up.
Model Parameter Setup
The following model parameters are made use of in the examples of mass transport boundary conditions. These parameters define the simulation domain 
and the simulation end time 
.
In some examples a smoothed step function 
will be used to prescribe a time profile for a transient parameter such as for example the mass flux 
or the concentration 
on the boundary. The smoothed step function is defined as follows:
Here the minimum value and the maximum value of the function 
can reach are denoted by 
and 
. The location of the step is controlled by 
and the smoothed steepness is controlled by 
.
Concentration Boundary Condition
Purpose
The purpose of a concentration boundary condition is to set a specific species concentration on some part of the boundary.
Formulation
With a specified concentration 
on the boundary 
, the concentration boundary condition is given for both conservative and non-conservative models by:
Since the concentration boundary condition is a Dirichlet type condition and thus is not associated with the model equation, its formulation is the same for both the conservative model and non-conservative model.
Derivation
We speak of a concentration boundary condition when a given species concentration 
is prescribed on a boundary. This prescribed concentration 
can either be a constant or time-dependent value, and is set with a DirichletCondition in the mass transport PDE model.
Example
To model, for example, the supply of a given species on a boundary, a transient species concentration 
can be set up at the left end. Note that a Neumann zero condition is implicitly applied at the right end as an outflow boundary.
Here a smoothed step function is used to described the profile of the species concentration 
on the boundary from 
to 
. The parameters 
and 
are arbitrarily chosen to simulate the supply of species from the boundary.
Next we set up the mass transport model with a flow field 
, an initial concentration field 
and a diffusion coefficient 
.
Visualization
The simulation begins with an undisturbed domain where 
. As the concentration 
increases at the left boundary, the excess species are then transported to the right and brings up the overall species concentration within the domain. The speed of the mass transport depends on the species diffusivity 
and the flow field.
Outflow Boundary Condition
Purpose
If the mass transport occurs in a system where the flow velocity 
, then an outflow boundary condition is used to model an outlet where the species can leave the domain with the fluid flow.
Formulation
When modeling mass transport in a fluid medium, the outflow boundary condition at the outlet 
is given by:
Note that for non-conservative model an outflow boundary condition is essentially a Neumann zero condition, which means it will be implicitly applied if no boundary condition is specified at a given boundary.
Derivation
When modeling mass transport with a fluid flow, the diffusion mass flux at the flow outlet is set to zero to ensure that the mass transferred at the outlet boundary is by mass convection only and the mass diffusion is ignored: 
.
With the non-conservative formulation, the NeumannValue[val,X∈Γb] specifies the boundary values (32): 
. So for 
we require 
to be 
. The outflow boundary condition for the non-conservative mass transport model is given by:
With the conservative formulation the NeumannValue[val,X∈Γb] specifies the boundary values (33): 
For 
we require:
The outflow boundary condition can only be applied on fully-developed flows. That is, at the flow outlet the velocity profile 
is unchanging in the flow direction.
In a case where there is recirculation through the outlet boundary, which often happens for turbulent flow, the reentering flow will affect the concentration field of the flow inside the domain and break the zero diffusion flux assumption. In this situation the outflow boundary condition is no longer applicable.
Example
In the following example an outflow boundary condition will be set at the left end to model the outgoing mass flux from the domain. We will present the boundary condition setup for both conservative model and non-conservative model.
To highlight the effect of an outflow boundary, we assume the species diffusivity 
to be zero. Therefore the mass transport is by convection only with the fluid flow 
.
We will use a concentration boundary condition to model the supply of a species into the domain from the right side.
Next we will present the boundary condition setup for both conservative model and non-conservative model. Note, that besides adding a conservative model form both setups, that are to follow, are the same.
Conservative Mass Transport Model with an Outflow Boundary Condition
and a normal 
at the outlet.
A message is generated to indicate that the PDE model is convection dominated. This is expected since there is no diffusion mass flux in this case, but is stable for this example. More information about this issue can be found in the Finite Element Usage Tips tutorial.
Non-Conservative Mass Transport Model with an Outflow Boundary Condition
If no boundary condition is specified on any part of the boundary then by default a Neumann zero boundary condition is implicitly used. This implies that an outflow boundary is the default boundary condition used for non-conservative mass transport model.
Visualization of an Outflow Boundary Condition
With an outflow boundary condition applied at the left boundary, the species was transported out of the domain by the fluid flow without reflection. Note that the results of conservative model and non-conservative model are consistent.
Mass Flux Boundary Condition
Purpose
The purpose of a mass flux boundary condition is to model the amount of a given species entering or leaving the domain through some part of the boundary.
Formulation
With a prescribed mass flux 
on the boundary 
, the mass flux boundary condition is given by:
Derivation
A boundary where the mass flux 
normal to the boundary is specified and not equal to zero is called a mass flux boundary:
By convention a negative sign is added in front of 
to indicates that the mass flux is specified opposite to the outward normal 
. Therefore, a positive value of 
denotes the inward mass flux where a given species enters the domain, and a negative 
denotes an outward flux.
As described in the previous section Transport Equation Derivation, the mass flux 
consists of the diffusion flux 
and the convection flux 
:
Recall that for the conservative formulation, the NeumannValue[val,X∈Γb] specifies the boundary values (34): 
. Therefore, by inserting (35) into (36), the mass flux boundary condition for the conservative model is given by:
In this case 
is 
and we have NeumannValue[
(t,X),X∈Γb].
For the non-conservative formulation the NeumannValue[val,X∈Γb] specifies the boundary values (37): 
. So by casting the boundary convection flux 
in (38) to the right hand side, the mass flux boundary condition for the non-conservative model is given by:
The unit of a mass flux 
depends on the dimension of the boundary. In 1D (
), 2D (
) and 3D domain (
), 
has a unit of 
, 
and 
, respectively.
Example
In the following example a transient mass flux 
is applied at the left boundary to model the supply of a species into the domain with no actual chemical reaction involved. The right boundary is set up as an outflow boundary condition to model the outgoing mass flux at the right end.
The profile of the mass flux is defined as:
Next we will present the boundary condition setup for both conservative model and non-conservative model. Note, that besides adding a conservative model form both setups, that are to follow, are the same.
Conservative Mass Transport Model with a Mass Flux Boundary Condition
Here we specify a flow field 
and an outflow boundary condition to model the outgoing mass flux at the right end.
The initial concentration field and the diffusion coefficient are given by 
and 
, respectively.
Non-Conservative Mass Transport Model with a Mass Flux Boundary Condition
and a normal 
at the outlet.Note that for non-conservative model an outflow boundary condition is a Neumann zero condition, and is implicitly applied at the right end of the domain.
Visualization of a Mass Flux Boundary Condition
With a mass flux 
applied at the left boundary, the species are gradually transported into the domain. After the mass flux is turned off at time 
, the remaining species continue to be transferred out of the domain with the fluid flow and the overall concentration field is brought down. Note that the results of the conservative model and the non-conservative model are consistent.
Impermeable Boundary Condition
The impermeable boundary condition is a special case of the mass flux boundary condition for the case where the flux across the boundary is 
.
Purpose
An impermeable boundary condition is to model a boundary where a species can not pass through and there is no mass flux across it.
Formulation
An impermeable boundary condition is given by:
Note that for a conservative model an impermeable boundary condition is essentially a Neumann zero condition, which means it will be implicitly applied if no boundary condition is specified at a given boundary.
Derivation
An impermeable boundary condition denotes a boundary where there is no mass flux across it:
By inserting (39) into the mass flux boundary condition (40), we yield the formulation of an impermeable boundary condition for both conservative and non-conservative models.
Example
In the following examples a Gaussian distribution is used to describe the initial concentration field 
within the domain, and an impermeable boundary is positioned on both ends to prohibit mass flux across boundaries.
To highlight the effect of an impermeable boundary, we assume that the flow field 
, which means that the mass transport is by diffusion only. The diffusion coefficient of the species is given by 
.
Next we will present the boundary condition setup for both conservative model and non-conservative model. Note, that besides adding a conservative model form both setups, that are to follow, are the same.
Conservative Mass Transport Model with an Impermeable Boundary Condition
If no boundary condition is specified on any part of the boundary then by default a Neumann zero boundary condition is implicitly used. This implies that an impermeable boundary is the default boundary condition when used for a conservative mass transport model.
Non-Conservative Mass Transport Model with an Impermeable Boundary Condition
Visualization of an Impermeable Boundary Condition
It is seen that the initial concentration field was gradually smoothed out by the internal diffusion, however, the net concentration within the domain remains unchanged. This is because there is no mass flux across the impermeable boundary on both ends. Note that the results of conservative model and non-conservative model are consistent.
Surrounding Flux Boundary Condition
A surrounding flux boundary condition is a flux condition applicable in the special case when the flow velocity field is zero 
. The surrounding flux boundary condition then extends a mass flux boundary condition for the case where the flux across the boundary depends on an exterior concentration 
and a mass transfer coefficient 
by: 
.
Purpose
A surrounding flux boundary condition is used to model mass transfer between the modeled system and the surrounding environment via diffusion across a boundary where the flow velocity is zero 
.
Formulation
Given the profile of an exterior concentration 
and a mass transfer coefficient 
on the boundary 
, the surrounding flux boundary condition is given by:
Since there is no fluid flow 
involved in the model, the formulation of the surrounding flux boundary condition is the same for both the conservative model and non-conservative model.
Derivation
When there is no fluid flow at the boundary, diffusion becomes the only mechanism for species to pass through the boundary. The rate of the diffusion flux across a boundary depends on the concentration gradient 
and physical properties of the transported species and properties of the medium, such as its phase and density.
Unfortunately, the relationship between the diffusion flux and these physical properties is not easily determined. To work around that the mass transfer coefficient 
is defined to lump these factors together. The diffusion mass flux can then be expressed as:
where 
is the exterior concentration in the surroundings of the modeled domain. The mass transfer coefficient 
can be determined experimentally [41, 42]. The mass transfer coefficient 
typically ranges from 
for gas phases to 
for liquid phases.
Inserting (43) into the mass flux boundary condition (44) and set the flow field 
, then the surrounding flux boundary condition can be written as:
Example
Consider a 1D example where carbon dioxide, 
, diffuses out of the domain from the left and right boundaries. The 
concentration outside the domain is comparably dilute and is assumed to be 
. The diffusion mass flux through the boundaries is modeled by a surrounding flux boundary condition with a given mass transfer coefficient 
.
In this case we use a Gaussian distribution to describe the initial concentration field 
, and the diffusion coefficient of 
is given by 
.
To better understand the effects of the surrounding flux boundary, we will compare the result of an analytical solution without any boundary condition. That is, the 
molecules keep diffusing out as if it had an infinite extent of the domain.
Visualization of a Surrounding Flux Boundary Condition
With surrounding flux conditions applied on both ends, the 
molecules were transported out of the domain at a faster rate than the one without it, which means the mass diffusion at boundaries is more efficient than the internal diffusion in this case.
Note that the diffusion flux to the surrounding environment varies from case to case, and is controlled by the values of the exterior concentration 
and the mass transfer coefficient 
.
With the surrounding flux condition the net concentration has been reduced from roughly 
to 
in three hours.
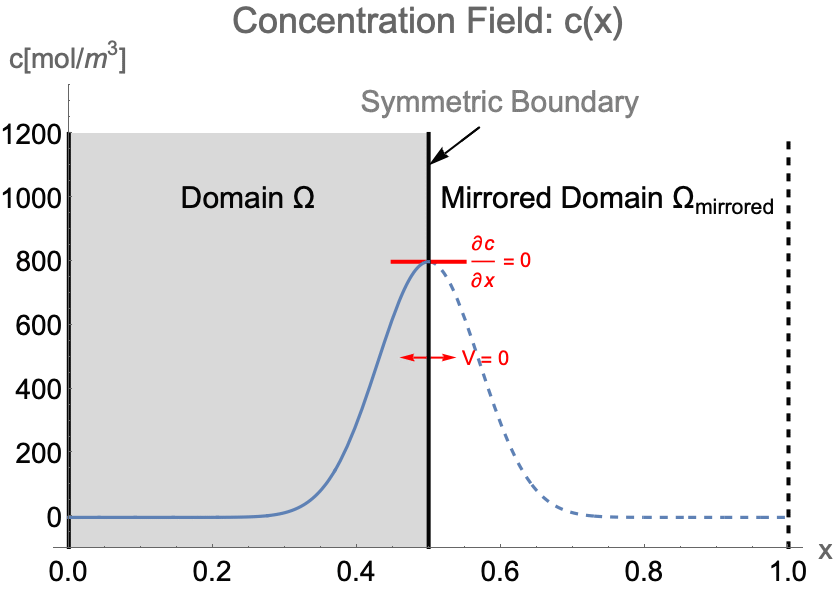
Symmetry Boundary Condition
Purpose
A symmetry boundary condition is used to reduce the extent of the computational domain to a symmetric sub-domain of the full physical model geometry by effectively reflecting across a linear boundary of the simulation domain where the flow velocity normal to the boundary is zero. This allows for a faster solution process with a lower memory requirement.
Formulation
The symmetry boundary condition is given by:
The formulation of the symmetry boundary condition is the same for both the conservative model and non-conservative model. Note that there is no boundary convection flux term 
in (45) since the normal flow velocity 
on the symmetry boundary will remain at zero at all time.
Note that a symmetry boundary condition is essentially a Neumann zero condition, which means it will be implicitly applied if no boundary condition is specified at a given boundary.
Derivation
To maintain the symmetry across a linear boundary, there should be no mass flux 
and no flow 
normal to the boundary at any time:
By inserting (46) into the mass flux boundary condition (47), the surrounding flux boundary condition can be written as:
Example
Consider the case of solving the concentration field of a 1D system from 
to 
. If the concentration pattern is expected to have a mirror symmetry along 
, we can efficiently construct the simulation domain 
with only the left half of the system. Then a symmetry boundary condition should be applied at 
.
Due to the symmetry, the concentration gradient 
and the flow velocity 
on the symmetry boundary will remain at zero at all time. Strictly speaking, a symmetry boundary is essentially an impermeable boundary. By setting the flow velocity 
to zero in the impermeable boundary condition (48), the symmetry boundary condition can be written as:
Periodic Boundary Condition
Purpose
The purpose of a periodic boundary condition is to map the species concentration from one boundary to another in order to exploit the periodicity of the domain.
Formulation
Given a function 
that maps the species concentration 
from the periodic boundary 
to the targeted boundary 
, the periodic boundary condition can be written as:
The formulation of a periodic boundary is the same for both the conservative model and non-conservative model.
Derivation
A periodic boundary condition is applied to compute mass transfer in spatially periodic domains. Given a targeted boundary 
, the species concentration 
on a periodic boundary can be mapped to the concentration 
on the targeted surface by a prescribed function 
. The boundary condition is set by the PeriodicBoundaryCondition in the mass transport PDE model.
Example
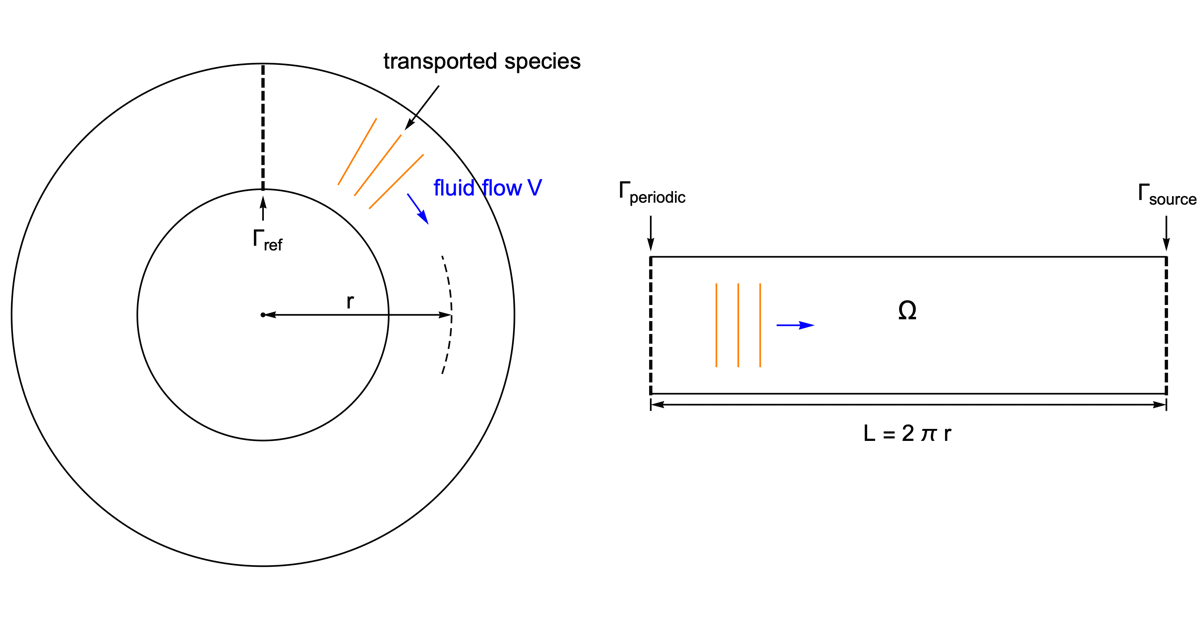
As an example we look at the species transportation within a circular tube. With the usage of the periodic boundary condition it is possible to perform the simulation in a 1D domain.
To highlight the effect of a periodic boundary, we assume the species diffusivity 
to be zero. Therefore the mass transport is by convection with the fluid flow 
only.
The circular tube is converted into a 1D model of the length 
equals to the perimeter of the tube. The periodic boundary 
is set at the left end so that when the species pass through the right side of the domain 
, it re-appears at the left side with the same magnitude.
Next we use a Gaussian distribution as the initial concentration field 
.
A message is generated to indicate that the PDE model is convection dominated. This is as expected since there is no diffusion mass flux in this case. More information about this issue can be found in the Finite Element Usage Tips tutorial.
Visualization of a Periodic Boundary Condition
It is seen that the species was transported to the right by the fluid flow within a spatially periodic domain. As the species pass through the right boundary it re-appears at the left side because of the periodicity of the domain set up with the periodic boundary condition. Since the species diffusivity is set as zero and the mass transported is by convection only, the pattern and the magnitude of the species concentration remains constant at all times.
Appendix
Special Cases of the Mass Balance Equation
As presented in the section Mass Balance Equation Derivation, the conservative and non-conservative forms of the mass balance equation are given by:
In the following sections we will present special cases of the mass balance equation and how it can be expressed in cylindrical coordinates and spherical coordinates.
Stationary Case
If the concentration field is in a steady state, the transient terms in the mass balance equation (49) and (50) vanish and the mass balance equation simplifies to:
Mass Transport by Diffusion Only
If the mass transport occurs in a solid medium, then, because a solid can not have an internal velocity field 
by definition, the convection terms in the mass balance equation (51) and (52) are set to zero, yielding:
In this case the mass transport is by diffusion only.
Mass Transport by Convection Only
When modeling mass transport by fluid flow, the diffusion term may be ignored if the mass transport is dominated by the mass convection, leading to:
In this case the mass transport is by convection only.
In a situation where the convection components 
and 
become large, the mass transport model will result in convection dominated PDEs. The solution of this type of PDEs may become unstable and extra stabilization methods may be needed. More information about this issue can be found in the Finite Element Usage Tips tutorial.
Mass Balance Equation in Cylindrical Coordinates
When modeling a mass transport problem, sometimes it is not convenient to describe the model in Cartesian coordinates. The heat equation may also be expressed using a cylindrical or spherical coordinate system.
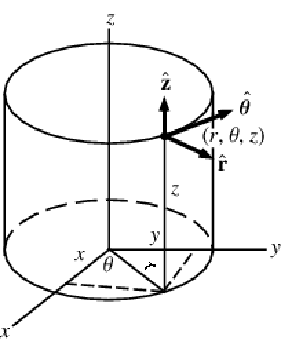
A graphics showing cylindrical coordinates:
In the cylindrical coordinate system 
, 
and 
denote the radial, azimuthal and vertical directions, respectively. In terms of the Cartesian coordinates 
, the cylindrical coordinates are defined by:
By inserting the coordinates relation (53) into equation (54) and (55), the mass balance equation can be expressed in cylindrical coordinates 
as:
If the mass transport within a model is rotationally symmetric about the 
axis, the resulting concentration field 
will be invariant in the 
direction. Equation (56) then simplifies to:
In that case, a 3D mass transport problem can be modeled in a 2D domain by making use of this symmetric property. This type of model is known as an axisymmetric model.
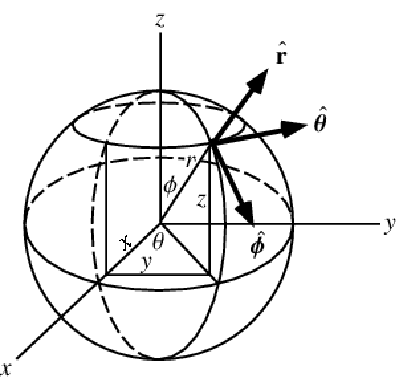
Mass Balance in Spherical Coordinates
A graphics showing spherical coordinates:
In the spherical coordinate system 
, 
and 
denote the radial, azimuthal and polar directions, respectively. In terms of the Cartesian coordinates: 
, the spherical coordinates are defined by:
By inserting the coordinates relation (57) into equation (58) and (59), the mass balance equation can be expressed in spherical coordinates 
as:
Nomenclature
References
1. Fick, A. Über Diffusion. Annalen der Physik (in German), 94 (1): 59–86 (1855).
2. Wolf, E. E. and Alfani, F. Catalysts Deactivation by Coking, Catalysis Reviews: vol 24 329-371 (1982).
3. Calvo, E. G., Arranz, M. A. and Leton, P. Effects of Impurities in the Kinetics of Calcite Decomposition, Thermochimica Acta. 170: 7–11 (1990).
4. Fu, J. C., Hagemeir, C. and Moyer, D. L., An unified mathematical model for diffusion from drug polymer composite tablets, Journal of Biomedical Materials Research: vol. 10, no. 5, pp. 743–758 (1976).
5. Parra-Guevara, D. and Skiba, Y. N. Elements of the mathematical modeling in the control of pollutants emissions, Ecological Modelling: vol. 167, no. 3, pp. 263–275 (2003).
6. Goldstein, R.J. and Cho, H. H. A review of mass transfer measurements using naphthalene sublimation, Experimental Thermal and Fluid Science: vol. 10, no. 4, pp. 416–434 (1995).
7. Cañizares, P., García-Gómez, J., Fernández de Marcos, I., Rodrigo, M. A. and Lobato, J. Measurement of Mass-Transfer Coefficients by an Electrochemical Technique, Journal of Chemical Education: vol. 83, no. 8 (2006).
8. LeVeque, R. J. Numerical Methods for Conservation Laws, Birkhduser (1992).
9. Whitman, G. Walter. The two film theory of gas absorption, International Journal of Heat and Mass Transfer: vol. 5, no. 5, pp. 429-433 (1962).
10. Prausnitz, J. M., Lichtenthaler R. N. and de Azevedo, E. G. Molecular Thermodynamics of Fluid Phase Equilibria 3rd Ed., Prentice Hall PTR, New Jersey (1999).