Gas Absorption at Liquid Surface
| Introduction | Solve the PDE Model |
| Domain | Post-processing and Visualization |
| Mesh Generation | Nomenclature |
| Mass Transport Model | References |
| Boundary Conditions |
Introduction
Physical and chemical gas absorption are an important separation processes and widely employed in various industries. Gas absorption is used to either separate undesirable components from a gas or for manufacturing purposes of chemicals.
This example reproduces a gas absorption model [1]. The absorption process takes place in the gas-liquid interface section shown below in gray:
A gas is exposed to a fully developed laminar flow. The gas flows either co-currently or counter-currently with respect to the flowing liquid. The above image displays the co-current case. The solute in the gas flow is absorbed and removed by the liquid flow beneath it, and mass transfer of the solute takes place from the gaseous to the liquid phase. The time of contact between solute and liquid is long enough to presume a parabolic velocity profile. Steady state conditions are assumed to prevail. In the post-processing section we will compare the absorption effectiveness between the co-current case and the counter-current case.
Domain
To model the interphase mass transfer, we will define a thin interphase region between the gas and liquid flow, which will allow us to enforce an equilibrium condition (1) specified below via coupled fictitious mass sources and handle the discontinuous concentration of the solute between two different phases.
Here we set the thickness 
of the interphase region to be 
of the height of the domain. Note that if 
is set too small numerical instability may occur around the interface.
Mesh Generation
We start be generating a boundary ElementMesh that accounts for the different material regions and the interface region. On the boundary we specify markers that will be used later to set up boundary conditions for to co-current and counter-current case.
To accurately model the mass transfer between the gas and liquid phases, the interphase region should be finely meshed. For clarity we add the material regions as an Association.
Mass Transport Model
A separate mass balance equation is used to describe the species concentration in the gas and liquid phases:
Here 
and 
are the concentration of solute dissolved in the gas phase and liquid phase. To model the mass transfer between the two phases we add coupling mass source terms 
and 
in the governing mass balance equation (2), leading to:
The above equations pose a system of 2 equations with each 3 material regions.
The diffusion coefficients of the solute in the gas and in the liquid phases are given by 
and 
respectively. Note that 
and 
are only active within the interphase region as well as their own phase.
Next, we specify the fluid flow velocities 
. The flow velocities are only active in their respective sub-regions. The gaseous flow velocity 
will initially be in the same direction as the liquid flow velocity 
.
To model the mass transfer between two phases we add the coupling mass source terms 
and 
in the governing mass balance equation (3), leading to:
Here 
and 
are set at 
so that the equilibrium condition (4): 
can be enforced at the interface.
In the equation 
is the interphase mass transfer coefficient, and 
is a switch that turns on 
within the interphase region and off 
otherwise.
Based on the two-resistance theory, the equilibrium at the interface is considered to be reached instantaneously and maintained at all times. This condition can be modeled by setting the mass transfer coefficient 
to be infinitely large. In practice, we can choose 
to be greater than the species diffusivity 
and 
) by several orders of magnitude.
At the interface of two phases the concentration 
and 
may be discontinuous. The ratio 
is known as the equilibrium distribution coefficient 
.
The coefficient 
depends on pressure, temperature and the chemical properties of the transported species and the media of both phases. The value 
can be determined by experimental measurement [2]. In this example the equilibrium coefficient is given by 
.
Due to mass conservation, the coupling source terms 
and 
have the same magnitude but opposite sign.
Also, see this note about how to set up of computationally efficient PDE coefficients.
Boundary Conditions
The concentration of solute is set at 
at the gas inlet, and 
at the liquid inlet.
Solve the PDE Model
Post-processing and Visualization
To measure the effectivity of the gas absorption, the net reduction of the solute is calculated between the gas inlet and outlet. For this the mean concentration at the outlet is computed with a boundary integration:
In the co-current case, the solute in the gas flow has been reduced by 
.
Next we compare the result with the case of counter-current gas and liquid flow.
In the counter-current case, the solute in the gas flow has been reduced by 
, which is more effective than the co-current case.
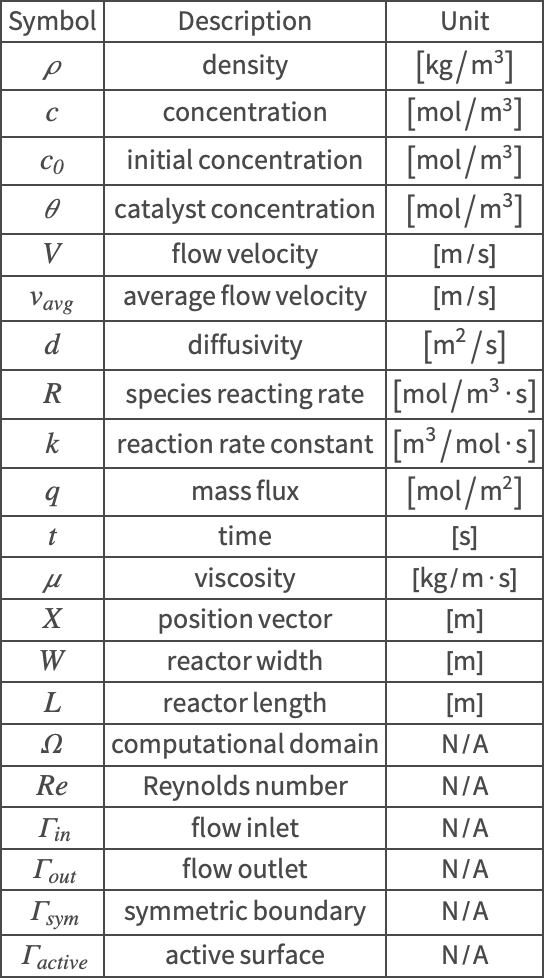
Nomenclature
References
1. Danish, M., Sharma, R.K. and Ali, S., Gas absorption with first order chemical reaction in a laminar falling film over a reacting solid wall, Applied Mathematical Modeling: 32 901–929 (2008).
2. Prausnitz, J. M., Lichtenthaler R. N. and de Azevedo, E. G. Molecular Thermodynamics of Fluid Phase Equilibria 3rd Ed., Prentice Hall PTR, New Jersey (1999).