Splines`
Splines`

SplineFit

As of Version 7.0, some of the functionality of the Splines Package is now built into the Wolfram Language kernel. »

SplineFit[{pt1,pt2,…},type]

generates a SplineFunction object of the specified type from the points pt1,pt2,….

Details and Options

  • To use SplineFit, you first need to load the Splines Package using Needs["Splines`"].
  • A SplineFunction object is a function that parametrizes a curve specified by the points pt1,pt2,…, such that an argument of 0 corresponds to pt1, 1 corresponds to pt2, etc.
  • Supported types are Cubic, Bezier and CompositeBezier.
  • A cubic spline is made of piecewise third‐order polynomials, with 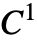C^(1) continuity, and interpolates each of the points it is created from. The second derivative of the spline at the endpoints is set to 0.
  • A Bézier spline interpolates only the endpoints. The other points control the spline, forming a convex hull. Given n points, a spline of degree n–1 is created.
  • A composite Bézier spline is made up of a series of third‐order Bézier curves with 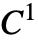C^(1) continuity. It alternates interpolating points and control points.
  • In a composite Bézier spline generated from an even number of points the last two points are reversed so that the final point is interpolated and the next to last is a control point for the final segment; if the spline is generated from an odd number of points, then the final vertex is doubled.
  • The points pt1,pt2,… are not restricted to two dimensions.

Examples

Basic Examples  (1)

SplineFit returns a SplineFunction of the appropriate type:

Fit three types of splines to a random set of five points:

Plot the resulting splines:

SplineFit works in arbitrary dimensions:

Wolfram Research (2008), SplineFit, Wolfram Language function, https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

Text

Wolfram Research (2008), SplineFit, Wolfram Language function, https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

CMS

Wolfram Language. 2008. "SplineFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/Splines/ref/SplineFit.html.

APA

Wolfram Language. (2008). SplineFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/Splines/ref/SplineFit.html

BibTeX

@misc{reference.wolfram_2024_splinefit, author="Wolfram Research", title="{SplineFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/Splines/ref/SplineFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_splinefit, organization={Wolfram Research}, title={SplineFit}, year={2008}, url={https://reference.wolfram.com/language/Splines/ref/SplineFit.html}, note=[Accessed: 21-November-2024 ]}