WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

ArcCurvature[{x1,…,xn},t]

パラメータ化された曲線（その直交座標 xi が t の関数である）の曲率を与える．

ArcCurvature[{x1,…,xn},t,chart]

xi を指定された座標チャート内の座標として解釈する．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

ArcCurvature

ArcCurvature[{x1,…,xn},t]

パラメータ化された曲線（その直交座標 xi が t の関数である）の曲率を与える．

ArcCurvature[{x1,…,xn},t,chart]

xi を指定された座標チャート内の座標として解釈する．

詳細

  • 弧の曲率は，符号なしの曲率あるいはフレネ(Frenet)曲率と呼ばれることがある．
  • 三次元ユークリッド空間における曲線 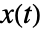の弧の曲率は，(TemplateBox[{{{{x, ^, {(, ', )}}, (, t, )}, x, {{x, ^, {(, {', '}, )}}, , {(, t, )}}}}, Norm])/(TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm]^3)で与えられる．
  • 一般空間では，曲線 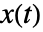の弧の曲率は，TemplateBox[{{{D, /, {(, {D, , t}, )}}, {{(, { , {{x, ^, {(, ', )}}, (, t, )}}, )}, /, {(, TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm], )}}}}, Norm]で与えられる．
  • ArcCurvature[x,t]では，x がスカラー式の場合は，ArcCurvatureはパラメトリック曲線{t,x}の曲率を与える．
  • ArcCurvatureの第3引数中の座標チャートは，CoordinateChartDataの第1引数におけるのと同じように，{coordsys,metric,dim}で指定することができる．dim を省略した短縮形を使うこともできる．

例題

すべて開く すべて閉じる

例  (2)

円は定曲率を持つ：

Wolfram Language code: ArcCurvature[{Sin[θ], Cos[θ]}, θ]

極座標で示されたフェルマの螺線の曲率：

Wolfram Language code: Simplify[ArcCurvature[{t, t^2}, t, "Polar"], t > 0]
Wolfram Language code: Simplify[ArcCurvature[{-t, t^2}, t, "Polar"], t > 0]

曲線の両方の枝を可視化する：

Wolfram Language code: PolarPlot[{Sqrt[t], -Sqrt[t]}, {t, 0, 4Pi}]

スコープ  (5)

球体上の航程線の曲率：

Wolfram Language code: ArcCurvature[{r Cos[t] / Cosh[Cot[b]t], r Sin[t] / Cosh[Cot[b]t], r Tanh[Cot[b]t]}, t]//Simplify
Wolfram Language code: Show[ParametricPlot3D[Table[{Cos[t] / Cosh[Cot[b]t], Sin[t] / Cosh[Cot[b]t], Tanh[Cot[b]t]}, {b, {Pi / 2 - .1, Pi / 2, Pi / 2 + .1}}]//Evaluate, {t, 0, 30}, PlotStyle -> Thick, PlotRange -> All], Graphics3D[{Opacity[.5], Sphere[]}]]

放物線の曲率は頂点で最大(2 TemplateBox[{a}, Abs])になり，無限大で0になる：

Wolfram Language code: ArcCurvature[a x ^ 2 + b x + c, x]
Wolfram Language code: Simplify[% /. x -> -b / (2a), a∈Reals]

測定基準，座標系，パラメータを指定する曲率：

Wolfram Language code: ArcCurvature[{1, t, 2t}, t, {{"Toroidal", {a}}, "Euclidean"}]

緯線と経線は平坦空間内または二次元球体上の曲線と考えることができる：

Wolfram Language code: Show[ParametricPlot3D[{{Cos[2 t]Sin[1], Sin[1]Sin[2 t], Cos[1]}, {Cos[1]Sin[t], -Sin[1]Sin[t], Cos[t]}}, {t, 0, π}, PlotStyle -> Thick, PlotLegends -> {"Parallel", "Meridian"}], Graphics3D[{Opacity[.5], Sphere[]}], PlotRange -> All]

三次元空間内の曲線と同じように，これらは，その半径に反比例する予想通りの曲率を持つ：

Wolfram Language code: ArcCurvature[{R Sin[θ] Cos[φ], R Sin[θ] Sin[φ], R Cos[θ]}, θ, "Cartesian"]//Simplify
Wolfram Language code: ArcCurvature[{R Sin[θ] Cos[φ], R Sin[θ] Sin[φ], R Cos[θ]}, φ, "Cartesian"]//Simplify

球体上では，測地線である経線の曲率は0であるが，赤道以外の緯線はそうではない：

Wolfram Language code: ArcCurvature[{θ, φ}, θ, {"Standard", {"Sphere", {R}}}]
Wolfram Language code: ArcCurvature[{θ, φ}, φ, {"Standard", {"Sphere", {R}}}]
Wolfram Language code: % /. θ -> π / 2

より高次元のユークリッド空間における曲率：

Wolfram Language code: ArcCurvature[{t, t ^ 2, t ^ 3, t ^ 4, t ^ 5}, t]

アプリケーション  (2)

ベルヌーイのレムニスケートの曲率半径を計算する：

Wolfram Language code: lem[t_] := (Cos[t]/1 + Sin[t]^2){1, Sin[t]}
Wolfram Language code: 1 / ArcCurvature[lem[t], t]//Simplify
Wolfram Language code: ParametricPlot[lem[t], {t, 0, 2Pi}]

Fary–Milnorの定理には，合計曲率 が より小さい閉曲線は結び目ではあり得ないとある．したがって，合計曲率が の円もまた結び目ではあり得ない：

Wolfram Language code: unknot = 2{Sin[#], Cos[#], 0}&
Wolfram Language code: Integrate[ArcCurvature[unknot[t], t] Norm[unknot'[t]], {t, 0, 2Pi}]

三つ葉結び目は少なくとも合計曲率が なければならない．そして，事実そうなっている：

Wolfram Language code: knot = KnotData["Trefoil", "SpaceCurve"]
Wolfram Language code: NIntegrate[ArcCurvature[knot[t], t] Norm[knot'[t]], {t, 0, 2Pi}]
Wolfram Language code: ParametricPlot3D[{knot[t], unknot[t]}, {t, 0, 2Pi}, PlotStyle -> {Thick, Directive[Thick, Dashed]}, PlotLegends -> {"Trefoil (Knot)", "Circle (Unknot)"}]

特性と関係  (2)

ArcCurvatureは単一の曲率のみを返す：

Wolfram Language code: ArcCurvature[{t, 0, -t ^ 2, 2t ^ 3}, t]

FrenetSerretSystemは，次元 で， 個の曲率すべてを返す：

Wolfram Language code: First[FrenetSerretSystem[{t, 0, -t ^ 2, 2t ^ 3}, t]]

ArcCurvatureには符号は付かない：

Wolfram Language code: ArcCurvature[{Sin[θ], Cos[θ]}, θ]
Wolfram Language code: ArcCurvature[{-Sin[θ], Cos[θ]}, θ]

FrenetSerretSystemから，二次元の符号付き曲率を抽出する：

Wolfram Language code: FrenetSerretSystem[{Sin[θ], Cos[θ]}, θ][[1, 1]]
Wolfram Language code: FrenetSerretSystem[{-Sin[θ], Cos[θ]}, θ][[1, 1]]
Wolfram Research (2014), ArcCurvature, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcCurvature.html.

テキスト

Wolfram Research (2014), ArcCurvature, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcCurvature.html.

CMS

Wolfram Language. 2014. "ArcCurvature." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArcCurvature.html.

APA

Wolfram Language. (2014). ArcCurvature. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcCurvature.html

BibTeX

@misc{reference.wolfram_2026_arccurvature, author="Wolfram Research", title="{ArcCurvature}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ArcCurvature.html}", note=[Accessed: 12-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_arccurvature, organization={Wolfram Research}, title={ArcCurvature}, year={2014}, url={https://reference.wolfram.com/language/ref/ArcCurvature.html}, note=[Accessed: 12-August-2026]}