FrenetSerretSystem[{x1,…,xn},t]
gives the generalized curvatures and Frenet–Serret basis for the parametric curve xi[t].
FrenetSerretSystem[{x1,…,xn},t,chart]
interprets the xi as coordinates in the specified coordinate chart.


FrenetSerretSystem
FrenetSerretSystem[{x1,…,xn},t]
gives the generalized curvatures and Frenet–Serret basis for the parametric curve xi[t].
FrenetSerretSystem[{x1,…,xn},t,chart]
interprets the xi as coordinates in the specified coordinate chart.
Details

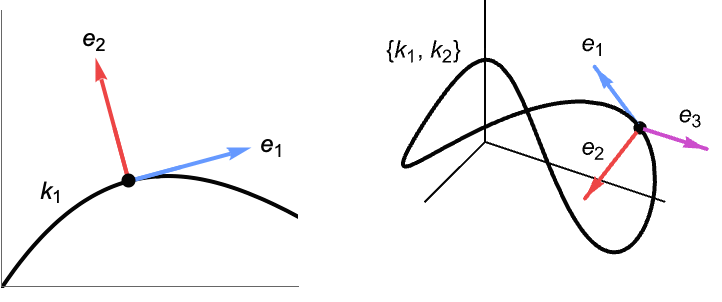
- FrenetSerretSystem returns {{k1,…,kn-1},{e1,…,en}}, where ki are generalized curvatures and ei are the Frenet–Serret basis vectors.
- The first basis vector e1 is the unit tangent to the curve. Each successive vector is the orthonormalized derivative of the previous one. The last vector is chosen to complete a right-handed orthonormal basis.
- If one of the vector derivatives is zero, then the remaining vectors are also taken to be zero.
- Common names in dimension two and three are:
-
{{k1},{e1,e2}} signed curvature, tangent, and normal {{k1,k2},{e1,e2,e3}} curvature, torsion, tangent, normal, and binormal - In FrenetSerretSystem[x,t], if x is a scalar expression, FrenetSerretSystem gives the curvature of the parametric curve {t,x}.
- If a chart is specified, the basis vectors ei are expressed in the orthonormal basis associated to it.
- Coordinate charts in the third argument of FrenetSerretSystem can be specified as triples {coordsys,metric,dim} in the same way as in the first argument of CoordinateChartData. The short form in which dim is omitted may be used.
Examples
open all close allBasic Examples (2)
Scope (6)
A straight line is degenerate, and so the basis is padded with zero vectors:
Curvature, torsion, and associated basis of a spiral restricted to a plane:
Construct the unit normal and tangent to the parabola ![]() :
:
The Frenet–Serret system specifying metric, coordinate system, and parameters:
A curve with nonzero tangent, normal, binormal, and trinormal:
FrenetSerretSystem works in curved spaces:
Applications (3)
Determine if two space curves intersect in a plane by checking the equality of their binormals:
Two curves in Euclidean space can be overlaid by rigid motion if and only if their curvatures are equal as functions of arc length:
As parameterized, the curves appear to have different curvatures:
But re-expressing the curvatures in terms of arc length shows that the curves are related by a rigid motion:
Construct an osculating circle, which is the circle that best approximates the curve at a point:
The radius of the osculating circle is inverse to the curvature:
The center of the circle lies along the normal to the curve at the contact point:
Plot the curve with two osculating circles and points of contact:
Properties & Relations (7)
In dimension ![]() , the first
, the first ![]() curvatures are always non-negative, but the last can be negative:
curvatures are always non-negative, but the last can be negative:
In two dimensions, the curvature is signed:
In dimensions three and higher, the ArcCurvature is the first generalized curvature:
In dimension two, the ArcCurvature is the absolute value of the single generalized curvature:
In two dimensions, the normal is always rotated counterclockwise relative to the tangent:
When the curve is embedded in three-space, the normal can be rotated in either direction:
The change in direction happens when the curvature crosses zero:
The normal and binormal are undefined at the crossing, then reverse direction:
In Euclidean space, if only the last curvature is identically 0, the curve lies in a hyperplane:
That hyperplane is perpendicular to the last basis vector, in this case the binormal:
Plot the plane containing the curve, using a point on the curve and the tangent and normal at that point:
The curve, hyperplane, and binormal:
For a curve embedded in nonplanar surface, no basis vector other than the tangent needs to maintain a constant angle to the surface:
Interactive Examples (1)
See Also
ArcCurvature ArcLength CoordinateChartData KnotData D Orthogonalize CoordinateTransform
Function Repository: FrenetSerretPlot MovingOrthonormalFrame BinormalVector Curvature CurveTorsion SecondFundamentalFormCoefficients NormalVector TangentVector DarbouxVector CurvatureTorsionPlot3D WhewellEquation
Related Guides
History
Text
Wolfram Research (2014), FrenetSerretSystem, Wolfram Language function, https://reference.wolfram.com/language/ref/FrenetSerretSystem.html.
CMS
Wolfram Language. 2014. "FrenetSerretSystem." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrenetSerretSystem.html.
APA
Wolfram Language. (2014). FrenetSerretSystem. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrenetSerretSystem.html
BibTeX
@misc{reference.wolfram_2025_frenetserretsystem, author="Wolfram Research", title="{FrenetSerretSystem}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FrenetSerretSystem.html}", note=[Accessed: 03-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_frenetserretsystem, organization={Wolfram Research}, title={FrenetSerretSystem}, year={2014}, url={https://reference.wolfram.com/language/ref/FrenetSerretSystem.html}, note=[Accessed: 03-January-2026]}