ButterworthFilterModel
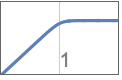
creates a lowpass Butterworth filter of order n and cutoff frequency of 1.
ButterworthFilterModel[{n,ωc}]
uses the cutoff frequency ωc.
ButterworthFilterModel[{"type",spec}]
creates a filter of a given "type" using the specified parameters spec.
ButterworthFilterModel[{"type",spec},var]
expresses the model in terms of the variable var.
Details



- ButterworthFilterModel returns the filter as a TransferFunctionModel.
- ButterworthFilterModel[{n,ω}] returns a lowpass filter with attenuation of
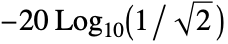 (approximately 3 dB) at frequency ω.
(approximately 3 dB) at frequency ω. - ButterworthFilterModel[n] uses the cutoff frequency of 1.
- Lowpass filter specification {"type",spec} can be any of the following:
-
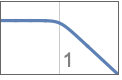
{"Lowpass",n} lowpass filter of order n and cutoff frequency 1 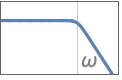
{"Lowpass",n,ωp} use cutoff frequency ωp 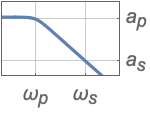
{"Lowpass",{ωp,ωs},{ap,as}} use full filter specification giving passband and stopband frequencies and attenuations - Highpass filter specifications:
-
{"Highpass",n} highpass filter with cutoff frequency 1 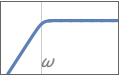
{"Highpass",n,ωp} use cutoff frequency ωp 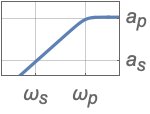
{"Highpass",{ωs,ωp},{as,ap}} full filter specification - Bandpass filter specifications:
-
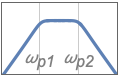
{"Bandpass",n,{ωp1,ωp2}} bandpass filter with passband frequencies ωp1 and ωp2 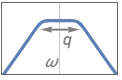
{"Bandpass",n,{{ω,q}}} use center frequency ω and quality factor q 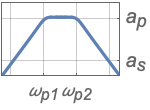
{"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}} full filter specification - Bandstop filter specifications:
-

{"Bandstop",n,{ωp1,ωp2}} bandstop filter with passband frequencies ωp1 and ωp2 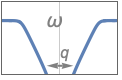
{"Bandstop",n,{{ω,q}}} use center frequency ω and quality factor q 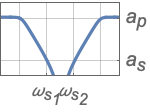
{"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}} full filter specification - Values ap and as are, respectively, absolute values of passband and stopband attenuations.
- Given a gain fraction
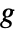 , the attenuation is
, the attenuation is 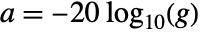 .
. - The quality factor q is defined as
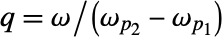 , with
, with 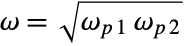 being the center frequency of a bandpass or bandstop filter. Higher values of q give narrower filters.
being the center frequency of a bandpass or bandstop filter. Higher values of q give narrower filters.
Examples
open allclose allBasic Examples (2)
Scope (6)
A symbolic lowpass Butterworth filter of order 3 with a cutoff frequency ω:
Same filter using the full specification:
Create a highpass Butterworth filter of order 3 with a cutoff frequency of 10:
Same filter using the full specification:
Create a "Bandpass" filter with passband frequencies ![]() and
and ![]() and attenuation of order 3:
and attenuation of order 3:
Same filter using center frequency and quality factor specification {{ω,q}}:
Same filter using the full specification:
Create a bandstop Butterworth filter:
Exact computation of the model:
Applications (6)
Create a lowpass Butterworth filter:
Filter out high-frequency noise from a sinusoidal signal:
Butterworth filter phase shifts the response by Arg[tf[ω ]], where ω is the frequency of the input sinusoid:
Create a highpass Butterworth filter from the lowpass prototype:
Filter out low-frequency sinusoid from the input:
Design a digital FIR lowpass filter using the Butterworth approximation that satisfies the following passband and stopband frequencies and attenuations:
Obtain the equivalent analog frequencies assuming a sampling period of 1:
Compute the analog Butterworth transfer function:
Convert to discrete-time model:
Create an FIR approximation of a discrete-time Butterworth IIR filter.
Implement a lowpass digital Butterworth filter:
Obtain the desired number of FIR samples from the impulse response of the discrete-time Butterworth filter:
Smooth financial data using an FIR approximation of a Butterworth filter:
Filter an image using a discrete-time lowpass Butterworth filter:
Properties & Relations (9)
Stopband attenuation increases by a factor of ![]() per decade as order
per decade as order ![]() increases:
increases:
Passband width of "Bandpass" filter decreases with increasing quality factor q:
Phase response of a third-order lowpass Butterworth filter:
Compare phase responses for different filter orders:
Phase response of a "Bandpass" filter for several quality factors:
Extract the order of the Butterworth polynomial:
The order of the Butterworth polynomial for lowpass and highpass is the same as the specified order:
The filter order for bandpass and bandstop is twice the given order:
Show the Butterworth polynomial in the denominator of the transfer function:
Find the poles of a Butterworth filter by solving for the roots of the denominator:
Extract poles using TransferFunctionPoles:
Plot poles of the Butterworth filter:
Implement a lowpass digital Butterworth filter:
Text
Wolfram Research (2012), ButterworthFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (updated 2016).
CMS
Wolfram Language. 2012. "ButterworthFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ButterworthFilterModel.html.
APA
Wolfram Language. (2012). ButterworthFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ButterworthFilterModel.html