ButterworthFilterModel
创建阶数为 n、截止频率为 1 的低通 Butterworth 滤波器.
ButterworthFilterModel[{n,ωc}]
使用截止频率 ωc.
ButterworthFilterModel[{"type",spec}]
使用指定参数 spec 创建已知 "type" 的滤波器.
ButterworthFilterModel[{"type",spec},var]
以变量 var 的形式表示模型.
更多信息



- ButterworthFilterModel 以 TransferFunctionModel 形式返回滤波器.
- ButterworthFilterModel[{n,ω}] 返回频率 ω 处衰减量为
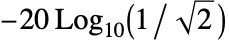 (约为3 dB)的低通滤波器.
(约为3 dB)的低通滤波器. - ButterworthFilterModel[n] 使用截止频率 1.
- 低通滤波器规范 {"type",spec} 可以是以下任何形式之一:
-
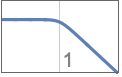
{"Lowpass",n} 阶数为 n、截止频率为1的低通滤波器 
{"Lowpass",n,ωp} 使用截止频率 ωp 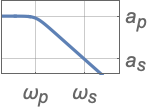
{"Lowpass",{ωp,ωs},{ap,as}} 使用完整滤波器规范,给出带通和带阻频率和衰减量 - 高通滤波器规范:
-
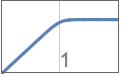
{"Highpass",n} 截止频率为1的高通滤波器 
{"Highpass",n,ωp} 使用截止频率 ωp 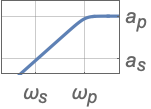
{"Highpass",{ωs,ωp},{as,ap}} 完整滤波器规范 - 带通滤波器规范:
-
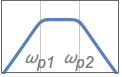
{"Bandpass",n,{ωp1,ωp2}} 带通频率为 ωp1 和 ωp2 的带通滤波器 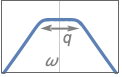
{"Bandpass",n,{{ω,q}}} 使用中心频率 ω 和质量因子 q 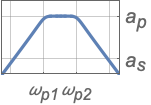
{"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}} 完整滤波器规范 - 带阻滤波器规范:
-
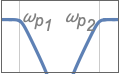
{"Bandstop",n,{ωp1,ωp2}} 带通频率为 ωp1 和 ωp2 的带阻滤波器 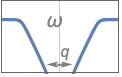
{"Bandstop",n,{{ω,q}}} 使用中心频率 ω 和质量因子 q 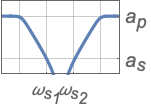
{"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}} 完整滤波器规范 - 值 ap 和 as 分别是带通和带阻衰减量的绝对值.
- 已知增益比率
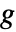 ,衰减量为
,衰减量为 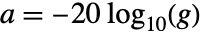 .
. - 质量因子 q 定义为
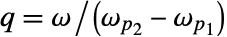 ,其中
,其中 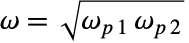 是带通或带阻滤波器的中心频率. q 值越高滤波器越窄.
是带通或带阻滤波器的中心频率. q 值越高滤波器越窄.
范例
打开所有单元关闭所有单元范围 (6)
应用 (6)
Butterworth 滤波器相位把响应移动了 Arg[tf[ω ]],其中 ω 是输入正弦波的频率:
使用 Butterworth 近似设计一个符合下列传输频带和抑止频带的频率和信号衰减的数字 FIR 低通滤波器:
创建离散时间 Butterworth IIR 滤波器的 FIR 近似.
从离散时间 Butterworth 滤波器的脉冲响应中获取 FIR 样本的所需数量:
使用 Butterworth 滤波器的 FIR 近似对金融数据进行平滑处理:
属性和关系 (9)
文本
Wolfram Research (2012),ButterworthFilterModel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (更新于 2016 年).
CMS
Wolfram 语言. 2012. "ButterworthFilterModel." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ButterworthFilterModel.html.
APA
Wolfram 语言. (2012). ButterworthFilterModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ButterworthFilterModel.html 年