CantorMesh
CantorMesh[n]
カントール(Cantor)集合のステップ n を表すメッシュ領域を与える.
CantorMesh[n,d]
次元 d のカントール集合のステップ n を与える.
詳細とオプション

- CantorMeshは,カントールダストとしても知られている.
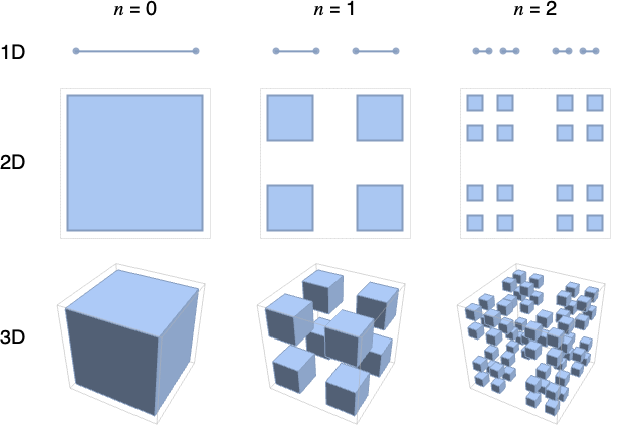
- CantorMesh[n]は,三等分したセルの中央部分を繰り返し取り除いて,単位区間から生成する. »
- CantorMesh[n]はCantorMesh[n,1]に等しい.
- CantorMeshにはMeshRegionと同じオプションに次を加えたものが使える.
-
DataRange Automatic 生成するメッシュ座標範囲
例題
すべて開くすべて閉じるオプション (13)
DataRange (1)
DataRangeを使うと生成するメッシュ座標の範囲を指定することができる:
MeshCellHighlight (2)
MeshCellLabel (2)
MeshCellMarker (1)
MeshCellMarkerを使ってCantorMeshに部分的に値を割り当てることができる:
MeshCellLabelを使ってマーカーを表示する:
MeshCellShapeFunction (2)
MeshCellStyle (3)
MeshCellStyleを使ってCantorMeshの部分的なスタイルを指定することができる:
アプリケーション (4)
特性と関係 (4)
CantorMeshの出力は,常に全次元のMeshRegionである:
1Dでは,CantorMeshは区間からなる:
DataRange->range はRescalingTransform[{…},range]を使うことに等しい:
考えられる問題 (1)
CantorMeshは大きすぎて生成できないことがある:
テキスト
Wolfram Research (2017), CantorMesh, Wolfram言語関数, https://reference.wolfram.com/language/ref/CantorMesh.html.
CMS
Wolfram Language. 2017. "CantorMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CantorMesh.html.
APA
Wolfram Language. (2017). CantorMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CantorMesh.html