

Ceiling 
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- Ceiling[x] can be entered in StandardForm and InputForm as ⌈x⌉,
 lc
lc
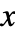
 rc
rc or
or
\[LeftCeiling]x \[RightCeiling]. » - Ceiling[x] returns an integer when
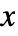 is any numeric quantity, whether or not it is an explicit number.
is any numeric quantity, whether or not it is an explicit number. - Ceiling[x] applies separately to real and imaginary parts of complex numbers.
- If a is not a positive real number, Ceiling[x,a] is defined by the formula Ceiling[x,a]a Ceiling[x/a]. »
- For exact numeric quantities, Ceiling internally uses numerical approximations to establish its result. This process can be affected by the setting of the global variable $MaxExtraPrecision.
- Ceiling automatically threads over lists. »
Examples
open all close allBasic Examples (4)
Round up to the nearest integer:
Round up to the nearest multiple of 10:
Plot the function over a subset of the reals:
Use ![]() lc
lc![]() and
and ![]() rc
rc![]() to enter a short notation for Ceiling:
to enter a short notation for Ceiling:
Scope (30)
Numerical Evaluation (7)
Single-argument Ceiling always returns an exact result:
The two-argument form tracks the precision of the second argument:
Evaluate efficiently at high precision:
Ceiling can deal with real‐valued intervals:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix Ceiling function using MatrixFunction:
Compute average-case statistical intervals using Around:
Specific Values (6)
Visualization (4)
Function Properties (9)
Ceiling is defined for all real and complex inputs:
Ceiling can produce infinitely large and small results:
Ceiling is not an analytic function:
It has both singularities and discontinuities:
Ceiling is nondecreasing:
Ceiling is not injective:
Ceiling is not surjective:
Ceiling is neither non-negative nor non-positive:
Ceiling is neither convex nor concave:
TraditionalForm formatting:
Differentiation and Integration (4)
First derivative with respect to x:
First derivative with respect to a:
Definite integrals of Ceiling:
Applications (4)
Self‐counting sequence:
Minimal number of elements in a box according to the pigeonhole principle:
Properties & Relations (10)
Negative numbers round up to the nearest integer above:
For a>0, Ceiling[x,a] gives the least multiple of a greater than or equal to x:
For other values of a, Ceiling[x,a] is defined by the following formula:
For a<0, the result is less than or equal to x:
Ceiling[x,-a] is equal to Floor[x,a]:
Denest Ceiling functions:
Reduce equations containing Ceiling:
Ceiling function in the complex plane:
Ceiling can be represented as a DifferenceRoot:
The generating function for Ceiling:
The exponential generating function for Ceiling:
Possible Issues (1)
Ceiling does not automatically resolve the value:
Neat Examples (1)
Convergence of the Fourier series of Ceiling:
See Also
Floor IntegerPart FractionalPart Round Chop BinCounts Quantile FindDivisions
Function Repository: MinMaxRounded
Related Guides
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2007 (6.0)
Text
Wolfram Research (1988), Ceiling, Wolfram Language function, https://reference.wolfram.com/language/ref/Ceiling.html (updated 2007).
CMS
Wolfram Language. 1988. "Ceiling." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Ceiling.html.
APA
Wolfram Language. (1988). Ceiling. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ceiling.html
BibTeX
@misc{reference.wolfram_2025_ceiling, author="Wolfram Research", title="{Ceiling}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Ceiling.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ceiling, organization={Wolfram Research}, title={Ceiling}, year={2007}, url={https://reference.wolfram.com/language/ref/Ceiling.html}, note=[Accessed: 25-January-2026]}