Chebyshev1FilterModel
n 次のローパス第1種チェビシェフ(Chebyshev)フィルタを作る.
Chebyshev1FilterModel[{n,ωc}]
カットオフ周波数 ωcを使う.
Chebyshev1FilterModel[{"type",spec}]
指定されたパラメータ spec を使い,指定された"type"のフィルタを作成する.
Chebyshev1FilterModel[{"type",spec},var]
変数 var によってモデルを表す.
詳細



- Chebyshev1FilterModelはフィルタをTransferFunctionModelとして与える.
- Chebyshev1FilterModel[{n,ω}]は,周波数 ω での減衰
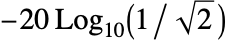 のローパスフィルタを返す.
のローパスフィルタを返す. - Chebyshev1FilterModel[n]はカットオフ周波数1を使う.
- ローパスフィルタ指定{"type",spec}には以下の任意のものを使うことができる.
-
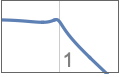
{"Lowpass",n} 次数 n,カットオフ周波数1のローパスフィルタ 
{"Lowpass",n,ωp} カットオフ周波数 ωpを使う 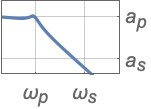
{"Lowpass",{ωp,ωs},{ap,as}} パスバンドとストップバンドの周波数と減衰を与える完全フィルタ指定を使う - ハイパスフィルタ指定
-
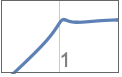
{"Highpass",n} カットオフ周波数1のハイパスフィルタ 
{"Highpass",n,ωp} カットオフ周波数 ωpを使う 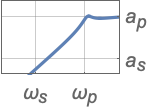
{"Highpass",{ωs,ωp},{as,ap}} 完全フィルタ指定 - バンドパスフィルタ指定
-

{"Bandpass",n,{ωp1,ωp2}} パスバンド周波数が ωp1と ωp2のバンドパスフィルタ 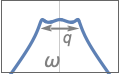
{"Bandpass",n,{{ω,q}}} 中心周波数 ω,Q値 q を使う 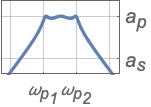
{"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}} 完全フィルタ指定 - バンドストップフィルタ指定
-

{"Bandstop",n,{ωp1,ωp2}} パスバンド周波数が ωp1と ωp2のバンドストップフィルタ 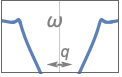
{"Bandstop",n,{{ω,q}}} 中心周波数 ω,Q値 q を使う 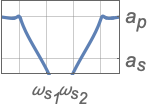
{"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}} 完全フィルタ指定 - 周波数値は昇順で与えられなければならない.
- 値 apと asはそれぞれパスバンドとストップバンドの減衰の絶対値である.
- ゲインが
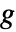 のとき,減衰は
のとき,減衰は 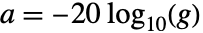 である.
である. - Q値 q は
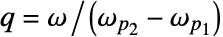 として定義される.ω はバンドパスフィルタあるいはバンドストップフィルタの中心周波数である.q の値が大きいほどフィルタは狭くなる.
として定義される.ω はバンドパスフィルタあるいはバンドストップフィルタの中心周波数である.q の値が大きいほどフィルタは狭くなる.
例題
すべて開くすべて閉じる例 (2)
スコープ (8)
アプリケーション (6)
第1種チェビシェフフィルタの位相は,Arg[tf[ω ]]による応答を移動させる.この場合,ω は入力正弦曲線の周波数である:
ローパスのプロトタイプからハイパスの第1種チェビシェフフィルタを作る:
次のパスバンド周波数,ストップバンド周波数,減衰を満足する第1種チェビシェフ近似を用いてデジタルFIRローパスフィルタを設計する:
サンプリング周期が1であると仮定して,上記と同等のアナログ周波数を得る:
離散時間第1種チェビシェフIIRフィルタのFIR近似を作る.
離散時間チェビシェフフィルタのインパルス応答から希望数のFIRサンプルを得る:
チェビシェフフィルタのFIR近似を使って金融データを平滑化する:
テキスト
Wolfram Research (2012), Chebyshev1FilterModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html (2016年に更新).
CMS
Wolfram Language. 2012. "Chebyshev1FilterModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html.
APA
Wolfram Language. (2012). Chebyshev1FilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html