Chebyshev1FilterModel

Chebyshev1FilterModel[n]

创建阶数为 n 的第一类切比雪夫低通滤波器.

Chebyshev1FilterModel[{n,ωc}]

使用截止频率 ωc.

Chebyshev1FilterModel[{"type",spec}]

使用指定参数 spec 设计已知 "type" 的滤波器.

Chebyshev1FilterModel[{"type",spec},var]

以变量 var 的形式表示模型.

更多信息

  • Chebyshev1FilterModel 以 TransferFunctionModel 返回滤波器.
  • Chebyshev1FilterModel[{n,ω}] 返回频率 ω 处衰减量为 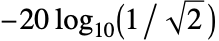（约为 3dB）的低通滤波器.
  • Chebyshev1FilterModel[n] 的截至频率为 1.
  • 低通滤波器规范 {"type",spec} 可以是下面所列的任何一种：
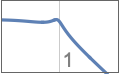
  • {"Lowpass",n}阶数为 n、截止频率为 1 的低通滤波器
    {"Lowpass",n,ωp}截至频率为 ωp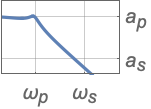
    {"Lowpass",{ωp,ωs},{ap,as}}使用完整的滤波器规范（给出通带和阻带的截至频率和衰减）
  • 高通滤波器规范：
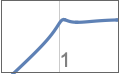
  • {"Highpass",n}截止频率为 1 的高通滤波器
    {"Highpass",n,ωp}截至频率为 ωp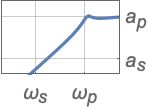
    {"Highpass",{ωs,ωp},{as,ap}}完整的滤波器规范
  • 带通滤波器规范：
  • {"Bandpass",n,{ωp1,ωp2}}通带频率为 ωp1 和 ωp2 的带通滤波器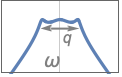
    {"Bandpass",n,{{ω,q}}}中心频率为 ω，品质因数为 q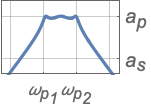
    {"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}}完整的滤波器规范
  • 带阻滤波器规范：
  • {"Bandstop",n,{ωp1,ωp2}}通带频率为 ωp1 和 ωp2 的带阻滤波器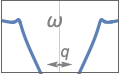
    {"Bandstop",n,{{ω,q}}}中心频率为 ω，品质因数为 q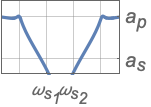
    {"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}}完整的滤波器规范
  • 频率值应该以升序给出.
  • 值 ap 和 as 分别是带通和带阻衰减量的绝对值.
  • 已知增益 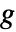，衰减量为 .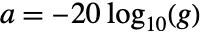
  • 品质因数 q 的定义为 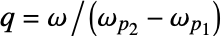，其中 ω 是带通或带阻滤波器的中心频率. q 的值越高，滤波器越窄.

范例

打开所有单元关闭所有单元

基本范例  (2)

三阶第一类切比雪夫滤波器模型：

所模拟的滤波器的波特幅值图：

使用完整规范设计第一类切比雪夫低通滤波器：

显示理想滤波器特征的幅值响应：

范围  (8)

设计符号式第一类切比雪夫滤波器模型：

提取模型的计算：

用 24 位精度计算模型：

使用变量 s 设计滤波器模型：

设计截止频率为 10 的第一类切比雪夫低通滤波器模型：

使用完整规范设计第一类切比雪夫低通滤波器：

设计第一类切比雪夫高通滤波器：

设计通带频率为 1 和 10 的 3 阶带通滤波器：

使用中心频率 1 和品质因数 1/3：

使用完整规范设计第一类切比雪夫带通滤波器：

设计第一类切比雪夫带阻滤波器：

应用  (6)

设计第一类切比雪夫低通滤波器：

滤除正弦信号中的高频噪声：

第一类切比雪夫滤波器把响应的相位平移了 Arg[tf[ω ]]，其中 ω 是输入正弦波的频率：

对相位平移进行校正：

根据低通原型设计第一类切比雪夫高通滤波器：

滤除输入中的低频正弦波：

用 Chebyshev 1 型近似设计一个数字 FIR 低通滤波器，满足以下通带和阻带频率以及衰减要求：

假定采样周期为 1，获取等价模拟频率：

计算模拟 Chebyshev 1 型转换函数：

转换成离散时间模型：

生成一个离散时间 Chebyshev 1 型 IIR 滤波器的 FIR 近似.

实现低通数字 Chebyshev 1 型滤波器：

从离散时间切比雪夫滤波器的冲激响应获取所需数量的 FIR 样本：

绘制 FIR 滤波器：

用切比雪夫滤波器的 FIR 近似平滑金融数据：

使用离散时间第一类切比雪夫低通滤波器对图像进行滤波：

使用第一类切比雪夫高通滤波器对图像进行滤波：

属性和关系  (8)

阻带衰减随阶数 n 的增加而增加：

"Bandpass" 滤波器的通带宽度随品质因数 q 的增加而减小：

三阶第一类切比雪夫 "Lowpass" 滤波器的相位响应：

比较不同阶数的滤波器的相位响应：

品质因数不同的 "Bandpass" 滤波器的相位响应：

比较第一类和第二类切比雪夫低通滤波器：

提取第一类切比雪夫多项式的次数：

求 Chebyshev 1 型滤波器的极点：

绘制 Butterworth 滤波器的极点：

实现低通数字 Chebyshev 1 型滤波器：

绘制数字 Chebyshev 1 型滤波器的极点：

把低通滤波器转化为高通滤波器：

Wolfram Research (2012)，Chebyshev1FilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html （更新于 2016 年）.

文本

Wolfram Research (2012)，Chebyshev1FilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html （更新于 2016 年）.

CMS

Wolfram 语言. 2012. "Chebyshev1FilterModel." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html.

APA

Wolfram 语言. (2012). Chebyshev1FilterModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html 年

BibTeX

@misc{reference.wolfram_2024_chebyshev1filtermodel, author="Wolfram Research", title="{Chebyshev1FilterModel}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_chebyshev1filtermodel, organization={Wolfram Research}, title={Chebyshev1FilterModel}, year={2016}, url={https://reference.wolfram.com/language/ref/Chebyshev1FilterModel.html}, note=[Accessed: 17-November-2024 ]}