CompleteGraphQ

CompleteGraphQ[g]

yields True if the graph g is a complete graph, and False otherwise.

CompleteGraphQ[g,vlist]

yields True if the subgraph induced by vlist is a complete graph, and False otherwise.

Details

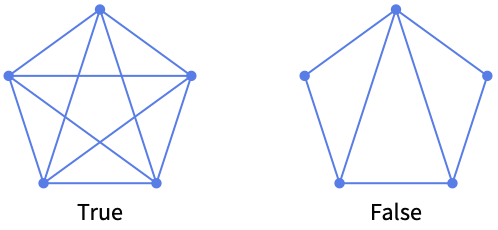
  • A graph is complete if there is an edge between every pair of distinct vertices.
  • CompleteGraphQ works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (2)

Test whether a graph is complete:

Petersen graph is not a complete graph:

Scope  (6)

Test undirected or directed graphs:

Multigraphs:

Mixed graphs:

Test subgraphs:

CompleteGraphQ gives False for anything that is not a complete graph:

Test large graphs:

Properties & Relations  (11)

A complete graph has no self-loops:

A TreeGraph is not a complete graph:

The only complete path graphs are triangles (undirected):

And the directed path:

A complete graph on vertices has edges:

The complete graph is a cycle graph :

The complete graph is a wheel graph :

The complete graph is the line graph of the star graph :

A complete graph is an -regular graph:

The GraphComplement of a complete graph is an empty graph:

For a complete graph, all entries outside the diagonal are 1s in the AdjacencyMatrix:

Complete graphs are their own cliques:

Wolfram Research (2010), CompleteGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/CompleteGraphQ.html (updated 2014).

Text

Wolfram Research (2010), CompleteGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/CompleteGraphQ.html (updated 2014).

CMS

Wolfram Language. 2010. "CompleteGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/CompleteGraphQ.html.

APA

Wolfram Language. (2010). CompleteGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompleteGraphQ.html

BibTeX

@misc{reference.wolfram_2025_completegraphq, author="Wolfram Research", title="{CompleteGraphQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CompleteGraphQ.html}", note=[Accessed: 20-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_completegraphq, organization={Wolfram Research}, title={CompleteGraphQ}, year={2014}, url={https://reference.wolfram.com/language/ref/CompleteGraphQ.html}, note=[Accessed: 20-February-2025 ]}