FindClique[g]
finds a largest clique in the graph g.
FindClique[g,n]
finds a clique containing at most n vertices.
FindClique[g,{n}]
finds a clique containing exactly n vertices.
FindClique[g,{nmin,nmax}]
finds a clique containing between nmin and nmax vertices.
FindClique[g,nspec,s]
finds at most s cliques.
FindClique[{g,v},…]
finds cliques that include the vertex v only.
FindClique[{vw,…},…]
uses rules vw to specify the graph g.


FindClique
FindClique[g]
finds a largest clique in the graph g.
FindClique[g,n]
finds a clique containing at most n vertices.
FindClique[g,{n}]
finds a clique containing exactly n vertices.
FindClique[g,{nmin,nmax}]
finds a clique containing between nmin and nmax vertices.
FindClique[g,nspec,s]
finds at most s cliques.
FindClique[{g,v},…]
finds cliques that include the vertex v only.
FindClique[{vw,…},…]
uses rules vw to specify the graph g.
Details

- A clique is a maximal set of vertices where the corresponding subgraph is a complete graph.
- FindClique returns a list of cliques.
- FindClique will return an empty list if there is no clique.
- FindClique[…,nspec,All] finds all the cliques.
- For weighted graphs, FindClique gives a set of vertices with maximum sum of vertex weights.
- FindClique works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.
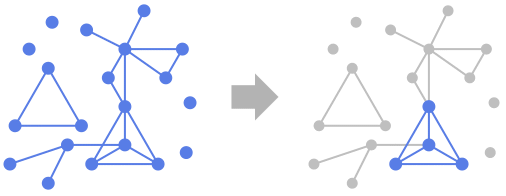
Background & Context
- FindClique finds a set of maximal cliques of specified size in a graph, returned as a list of vertex lists. Here, a clique is a subset of vertices such that the corresponding induced subgraph is a complete graph. Cliques are used in project selection, pattern matching, finance, and network analysis. In general, FindClique[g,nspec,s] finds a set of s maximal cliques of specified size nspec in a graph g.
- There are two especially important types of cliques: maximum and maximal. Note these are not equivalent. A maximum clique is a clique containing the largest possible number of vertices for a given graph. In contrast, a maximal clique set is a clique that cannot be extended by including one more adjacent vertices, meaning it is not a subset of a larger clique. A maximum clique is therefore always maximal (since it obviously cannot be extended if it is already of the maximum size), but the converse is not necessarily true. To confuse the terminology even more, some authors refer to maximum cliques simply as "cliques".
- FindClique can find maximal cliques of different sizes. FindClique can also find a single maximal clique of specified size, a specified number of cliques, or all such cliques.
- FindClique[g] finds a single maximum clique of a graph g, FindClique[g,Length/@FindClique[g],s] finds at most s, and FindClique[g,Length/@FindClique[g],All] finds all such cliques. The size of a maximum clique of a graph g is known as its clique number, and the problem of finding the size of a maximum clique for a given graph is NP-complete, meaning computation can be exponentially slow.
- FindClique[g,Infinity] finds a single maximal clique of a graph g, FindClique[g,Infinity,s] finds at most s, and FindClique[g,Infinity,All] finds all such cliques. Maximal cliques are important in graph theoretic applications, including graph coloring and fractional graph coloring.
- Not-necessarily-maximal cliques cannot be found directly using FindClique but can be simplistically enumerated by taking the union over the collection of all subsets of all maximal cliques.
- A maximal independent vertex set (which can be found using FindIndependentVertexSet) of a graph is equivalent to a maximal clique on its GraphComplement. A collection of vertices vlist of a graph g can be tested to see if it is a clique (without the requirement that it also be maximal) using CompleteGraphQ[g,vlist]. FindKClique, FindKClan, and FindKClub find clique-like structures that allow less-than-complete connections in subgraphs.
Examples
open all close allScope (14)
Specification (8)
FindClique works with undirected graphs:
Use rules to specify the graph:
FindClique works with large graphs:
Enumeration (6)
A clique containing exactly 3 vertices:
A clique containing at most 2 vertices:
A clique containing between 3 and 5 vertices:
A largest clique that includes a given vertex:
FindClique gives an empty list if there is no clique:
Applications (5)
Highlight all cliques in a graph:
Find a largest immediate family in a network consisting of the closest relatives, including parents, siblings, and children:
A network of books linked by the same buyers on Amazon.com. Find a largest selection of books frequently bought together that includes The Clinton Wars:
Find terrorist cells in the 1998 East Africa embassy attack network:
Show cooperating terrorist cells:
Find external contacts to isolate the Dar es Salaam attack cell:
Find members of the Dow Jones Industrial Average whose returns tend to move in sync:
First compute the correlation of returns since the beginning of this year:
Build a graph with edges between stocks having a correlation coefficient above a chosen ![]() :
:
Properties & Relations (8)
A clique is a maximal set of vertices that generates a complete subgraph:
{1,2,3} and {1,2,3,4} generate complete subgraphs but are not maximal:
The maximum clique is the largest clique:
The subgraph induced by a clique is a complete graph:
A clique in a graph is an independent vertex set of its complement graph:
The vertex complement of a clique in a graph is a vertex cover of its complement graph:
The largest clique in a complete graph has all its vertices:
A complete ![]() -partite graph has a maximum clique of size
-partite graph has a maximum clique of size ![]() :
:
The largest clique of size ![]() is contained in a
is contained in a ![]() -core component:
-core component:
All cliques are ![]() -cliques,
-cliques, ![]() -clans,
-clans, ![]() -clubs, and
-clubs, and ![]() -plexes for
-plexes for ![]() :
:
Conversely, all 1-cliques, 1-clans, 1-clubs, and 1-plexes are cliques:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2015 (10.3)
Text
Wolfram Research (2010), FindClique, Wolfram Language function, https://reference.wolfram.com/language/ref/FindClique.html (updated 2015).
CMS
Wolfram Language. 2010. "FindClique." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindClique.html.
APA
Wolfram Language. (2010). FindClique. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindClique.html
BibTeX
@misc{reference.wolfram_2025_findclique, author="Wolfram Research", title="{FindClique}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindClique.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_findclique, organization={Wolfram Research}, title={FindClique}, year={2015}, url={https://reference.wolfram.com/language/ref/FindClique.html}, note=[Accessed: 25-January-2026]}