CoulombG

CoulombG[l,η,r]

非正則クーロン(Coulomb)波動関数 TemplateBox[{l, eta, r}, CoulombG]を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • CoulombG[l,η,r]は常微分方程式 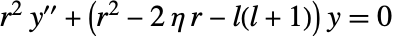の解である．
  • CoulombG[l,η,r]は大きい 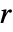と何らかの位相シフト についてになる傾向がある．
  • CoulombG[l,η,r]は 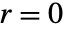に確定特異点を持つ．
  • CoulombGは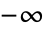からまでの複素 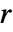平面上に不連続な分枝切断線を持つ．
  • CoulombGは特定の引数については自動的に厳密値に評価される．
  • CoulombGは任意の数値精度で評価することができる．
  • CoulombGは自動的にリストに縫い込まれる．
  • CoulombGはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (4)

数値的に評価する：

斥力()と引力()の相互作用についてクーロン波動関数をプロットする：

複素数プロット：

原点における級数展開：

大きい半径の漸近動作：

スコープ  (18)

数値評価  (5)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

CoulombGはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる：

特定の値  (2)

CoulombGは，パラメータ η の値が0のときはベッセル(Bessel)関数に簡約される：

CoulombGの最初の正の零点を求める：

可視化  (2)

CoulombG関数をプロットする：

TemplateBox[{2, 0, z}, CoulombG]の実部をプロットする：

TemplateBox[{2, 0, z}, CoulombG]の虚部をプロットする：

関数の特性  (7)

CoulombGの定義域：

CoulombGは η の解析関数である：

CoulombG[2,0,x]は単射ではない：

CoulombG[2,0,x]は非負でも非正でもない：

CoulombG[2,0,x]は零点に特異点と不連続点の両方を持つ：

CoulombGは凸でも凹でもない：

TraditionalFormによる表示：

級数展開  (1)

零点と無限大でSeriesを使ってテイラー(Taylor)展開を求める：

の周りのCoulombGの最初の3つの近似をプロットする：

関数表現  (1)

他のクーロン関数を介した表現：

アプリケーション  (2)

クーロン波動方程式を解く：

CoulombGのWKB近似を構築する：

WKB近似を実際の関数と比較する：

特性と関係  (1)

CoulombGはCoulombH1とCoulombH2の線形結合である：

Wolfram Research (2021), CoulombG, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoulombG.html （2023年に更新）.

テキスト

Wolfram Research (2021), CoulombG, Wolfram言語関数， https://reference.wolfram.com/language/ref/CoulombG.html （2023年に更新）.

CMS

Wolfram Language. 2021. "CoulombG." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CoulombG.html.

APA

Wolfram Language. (2021). CoulombG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoulombG.html

BibTeX

@misc{reference.wolfram_2024_coulombg, author="Wolfram Research", title="{CoulombG}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CoulombG.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coulombg, organization={Wolfram Research}, title={CoulombG}, year={2023}, url={https://reference.wolfram.com/language/ref/CoulombG.html}, note=[Accessed: 21-November-2024 ]}