CoulombG

CoulombG[l,η,r]

gives the irregular Coulomb wavefunction TemplateBox[{l, eta, r}, CoulombG].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • CoulombG[l,η,r] is a solution of the ordinary differential equation .
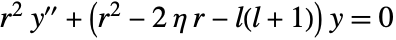  • CoulombG[l,η,r] tends to 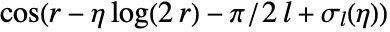for large 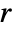and some phase shift .
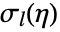  • CoulombG[l,η,r] has a regular singularity at .
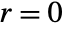  • CoulombG has a branch cut discontinuity in the complex 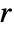plane running from 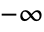to .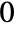
  • For certain special arguments, CoulombG automatically evaluates to exact values.
  • CoulombG can be evaluated to arbitrary numerical precision.
  • CoulombG automatically threads over lists.
  • CoulombG can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (4)

Evaluate numerically:

Plot the Coulomb wavefunction for repulsive () and attractive () interactions:

Complex plot:

Series expansion at the origin:

Asymptotic behavior for large radius:

Scope  (18)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

CoulombG can be used with Interval and CenteredInterval objects:

Specific Values  (2)

For a zero value of the parameter η, CoulombG reduces to a spherical Bessel function:

Find the first positive zero of CoulombG:

Visualization  (2)

Plot the CoulombG function:

Plot the real part of TemplateBox[{2, 0, z}, CoulombG]:

Plot the imaginary part of TemplateBox[{2, 0, z}, CoulombG]:

Function Properties  (7)

Function domain of CoulombG:

CoulombG is an analytic function of η:

CoulombG[2,0,x] is not injective:

CoulombG[2,0,x] is neither non-negative nor non-positive:

CoulombG[2,0,x] has both singularities and discontinuities at zero:

CoulombG is neither convex nor concave:

TraditionalForm formatting:

Series Expansions  (1)

Find the Taylor expansion using Series at zero and at infinity:

Plots of the first three approximations for CoulombG around :

Function Representations  (1)

Representation through other Coulomb functions:

Applications  (2)

Solve the Coulomb wave equation:

Construct a WKB approximation of CoulombG:

Compare the WKB approximation with the actual function:

Properties & Relations  (1)

CoulombG is a linear combination of CoulombH1 and CoulombH2:

Wolfram Research (2021), CoulombG, Wolfram Language function, https://reference.wolfram.com/language/ref/CoulombG.html (updated 2023).

Text

Wolfram Research (2021), CoulombG, Wolfram Language function, https://reference.wolfram.com/language/ref/CoulombG.html (updated 2023).

CMS

Wolfram Language. 2021. "CoulombG." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CoulombG.html.

APA

Wolfram Language. (2021). CoulombG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoulombG.html

BibTeX

@misc{reference.wolfram_2025_coulombg, author="Wolfram Research", title="{CoulombG}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CoulombG.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_coulombg, organization={Wolfram Research}, title={CoulombG}, year={2023}, url={https://reference.wolfram.com/language/ref/CoulombG.html}, note=[Accessed: 21-February-2025 ]}