CrossingPolygon

CrossingPolygon[{p₁,p₂,…,p_n}]

ある点から平面内の任意の方向に向けて出た半直線が，半直線{p₁,p₂},…,{p_n-1,p_n},{p_n,p₁}と偶数回交差するすべての点を表すPolygonを与える．

CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]

線分{p₁₁,p₁₂},…,{p₂₁,p₂₂},…からのPolygonを与える．

詳細とオプション

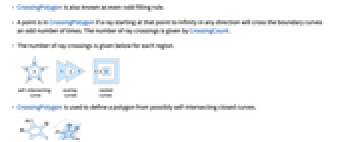
CrossingPolygonは偶奇充填規則としても知られている．
ある点から出て無限大の任意の方向に向かう半直線が境界曲線と偶数回交差するなら，その点はCrossingPolygon内にある．半直線の交差回数はCrossingCountで与えられる．
下の各領域についての半直線の交差回数

CrossingPolygonは，例えば自己交差のある曲線からの多角形の定義に使われる．

CrossingPolygon[{p₁,p₂,…,p_n}]は，事実上，Polygon[{p₁,p₂,…,p_n}]に等しい．
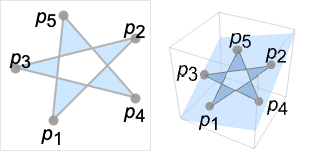
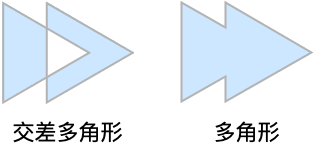
CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]は，一般に，Polygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]とは異なる．前者がすべての閉曲線{p_i1,p_i2,…}に対して半直線交差規則を使うのに対し，後者は多角形Polygon[{p_i1,p_i2,…}]の和集合であるからである．

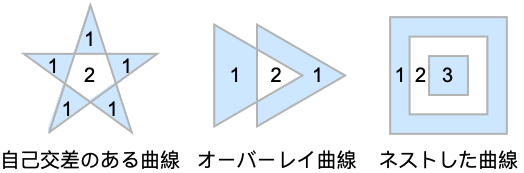
点 p_iは任意の長さでよいが，すべてが平面上になければならない．
CrossingPolygonはPolygonと同じオプションを取る．

全オプションのリスト

例題

すべて開くすべて閉じる

例 (2)

多角形を定義する：

自己交差する輪郭線から多角形を構築する：

その面積を計算する：

スコープ (11)

基本的な用法 (5)

二次元の多角形を定義する：

三次元の多角形：

次元の多角形：

自己交差する輪郭線から多角形を構築する：

複数の輪郭線：

自己交差する輪郭線 (3)

CrossingPolygonは自己交差する輪郭線に使うことができる：

重なり合う輪郭線の線分：

複数の輪郭線：

複数の輪郭線 (3)

CrossingPolygonは複数の輪郭線に使うことができる：

自己交差する輪郭線：

オプション (6)

VertexColors (2)

頂点が着色された多角形：

3D多角形の頂点の色を指定する：

VertexNormals (1)

辺ベクトルの外積を使って法線ベクトルを計算する：

法線が{1,-1,1}を指している三角形：

異なる法線を使うと陰影に影響がある：

VertexTextureCoordinates (3)

2D多角形のテクスチャマッピング：

3D多角形のテクスチャマッピング：

非統一テクスチャ座標値を使ってテクスチャを繰り返す：

VertexColorsはテクスチャマッピングに先立つ：

アプリケーション (3)

基本的なアプリケーション (1)

輪郭線からの多角形の構築：

コンピュータグラフィックス (1)

タートル描画多角形．20ステップ進む．常に左に110°曲がる：

計算幾何学 (1)

ランダムな多角形を生成する：

特性と関係 (3)

CrossingPolygonは，事実上，単一の輪郭線に関しては評価するとPolygonになる：

CrossingPolygonは，一般に，複数の交差がある輪郭線についてはPolygonとは異なる：

WindingPolygonは，別の多角形の輪郭線である：

考えられる問題 (1)

CrossingPolygon中の点はすべて平面上になければならない：

おもしろい例題 (1)

デジタル花弁：

トップへ