DerivativePDETerm
DerivativePDETerm[{u,{x1,…,xn}},γ]
荷重微分係数 ![]() ,モデル変数 vars の荷重微分項
,モデル変数 vars の荷重微分項 ![]() を表す.
を表す.
DerivativePDETerm[vars,γ,pars]
モデルパラメータ pars を使う.
詳細

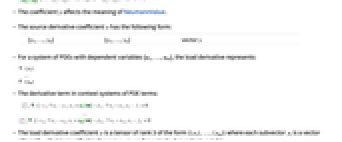

- 荷重微分はソースまたはシンクの微分のモデル化によく使われる.
- ソースの微分係数
 を使った微分の計算は,以下でモデル化されるソースの微分を加える過程である.
を使った微分の計算は,以下でモデル化されるソースの微分を加える過程である. - DerivativePDETermは,偏微分方程式の一部として使われる微分演算子項を返す.
- DerivativePDETermを使って,方程式の導関数が,従属変数
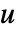 ,独立変数
,独立変数 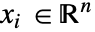 ,時間変数
,時間変数  でモデル化できる.
でモデル化できる. - 定常モデル変数 vars は vars={u[x1,…,xn],{x1,…,xn}}である.
- 時間依存モデル変数 vars は vars={u[t,x1,…,xn],{x1,…,xn}}または vars={u[t,x1,…,xn],t,{x1,…,xn}}である.
- 他のPDE項との関連によるソースの微分項
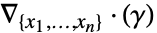 は以下で与えられる.
は以下で与えられる. - 係数
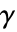 はNeumannValueの意味に影響を与える.
はNeumannValueの意味に影響を与える. - ソースの微分係数
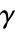 は次の形である.
は次の形である. -
{γ1,…,γn} 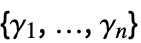
ベクトル 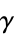
- 荷重項は,従属変数{u1,…,um}がある偏微分方程式系については以下を表す.
- 以下は,PDE項の系との関連における微分項である.
- 荷重微分係数
 は,形が
は,形が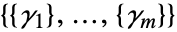 の3階のテンソルである.各部分ベクトル
の3階のテンソルである.各部分ベクトル 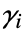 は,単一の従属変数と同じように指定される長さ
は,単一の従属変数と同じように指定される長さ 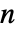 のベクトルである.
のベクトルである. - 荷重微分係数
 は,時間,空間,パラメータ,従属変数に依存することがある.
は,時間,空間,パラメータ,従属変数に依存することがある. - 次は,使用可能なパラメータ pars である.
-
パラメータ デフォルト シンボル "RegionSymmetry" None 
- パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は以下のように角度変数を除くことで円柱座標が縮小された切取り円柱座標系を表す.
-
次元 縮小 方程式 1D 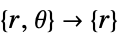
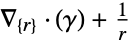
2D 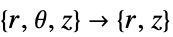
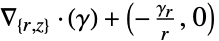
- 与えられた独立変数に明示的には依存しない数量はすべて,ゼロ偏微分を持つとみなされる.
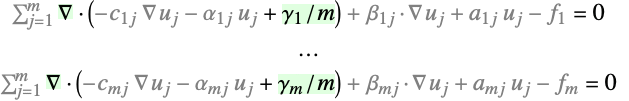
例題
すべて開くすべて閉じる例 (3)
スコープ (9)
その項にActivateを適用する:
軸対称の場合は微分項を構成する演算子を使って切取り円柱座標系を使った結果であることを確認する:
その項にActivateを適用する:
軸対称のケースは微分項を構成する演算子を使って切取り円柱座標系を使った結果であることを確認する:
DerivativePDETermを使って微分方程式成分の導関数が計算できる.変数,領域,境界条件を設定する:
DerivativePDETermで微分項の系を設定する:
テキスト
Wolfram Research (2020), DerivativePDETerm, Wolfram言語関数, https://reference.wolfram.com/language/ref/DerivativePDETerm.html.
CMS
Wolfram Language. 2020. "DerivativePDETerm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DerivativePDETerm.html.
APA
Wolfram Language. (2020). DerivativePDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DerivativePDETerm.html