LaplacianPDETerm

LaplacianPDETerm[vars]

represents a Laplacian term with model variables vars.

LaplacianPDETerm[vars,pars]

uses model parameters pars.

Details

  • The Laplacian term is a differential operator term used to describe many physical phenomena, such as potentials, heat transfer, acoustics, structural mechanics and fluid dynamics.
  • LaplacianPDETerm returns a differential operators term to be used as a part of partial differential equations:
  • LaplacianPDETerm can be used to model Laplacian equations with dependent variable 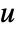, independent variables 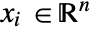and time variable .
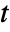  • Stationary model variables vars are vars={u[x1,…,xn],{x1,…,xn}}.
  • Time-dependent model variables vars are vars={u[t,x1,…,xn],{x1,…,xn}} or vars={u[t,x1,…,xn],t,{x1,…,xn}}.
  • The Laplacian 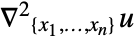is realized as a DiffusionPDETerm with 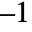as a diffusion coefficient resulting in .
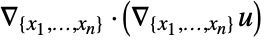  • The following parameters pars can be given:
  • parameterdefaultsymbol
    "RegionSymmetry"None
  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D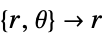
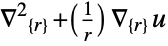
    2D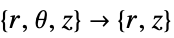
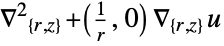
  • The diffusion coefficient affects the meaning of NeumannValue.

Examples

open allclose all

Basic Examples  (2)

Define a stationary Laplacian term:

Find eigenvalues of a Laplacian term:

Scope  (3)

Set up a time-dependent Laplacian:

Define a 2D axisymmetric stationary Laplacian term:

Activate the term:

Verify that the axisymmetric case is a consequence of using a truncated cylindrical coordinate system using the operators that compose the Laplacian term:

Find eigenvalues and vectors of a Laplacian term in a 3D shell:

Visualize the result:

Applications  (1)

Solve the Laplace equation for inside a finite cylinder of radius 5. The region of analysis is a 3D solid cylinder, but since the region is rotationally symmetric around the axis, an axisymmetric stationary LaplacianPDETerm can be used, and so the region can be defined with truncated cylindrical coordinates in 2D .

Set up the region:

Set up the PDE model:

Solve the equation and measure time and memory needed to do so:

Visualize the axisymmetric result:

Print the total time to do the computation and number of megabytes used during the evaluation:

The computational cost in time and memory to solve the 2D axisymmetric PDE model is much less than the full 3D model. Create the full 3D region:

Set up the 3D model:

Solve the full 3D model while at the same time improving the boundary position for optimal approximation of the symbolic region and a refinement in the critical area:

Print the total time to do the computation and number of megabytes used during the evaluation:

Visualize the result from the 3D solution:

Compare the timings and memory measurements for the two cases:

Visualize the difference between the two solutions:

Possible Issues  (1)

There is no axisymmetric 3D case:

Neat Examples  (1)

Find your way through a maze by solving a Laplace equation. Set up a maze:

Convert the graph of the maze to a mesh:

Solve a Laplace equation with the entrance as a DirichletCondition of value 1 and the exit as a DirichletCondition with value 0. Find the region bounds to set the position of the DirichletCondition:

Solve the equation:

Visualize the path through the maze:

Wolfram Research (2020), LaplacianPDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/LaplacianPDETerm.html (updated 2022).

Text

Wolfram Research (2020), LaplacianPDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/LaplacianPDETerm.html (updated 2022).

CMS

Wolfram Language. 2020. "LaplacianPDETerm." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/LaplacianPDETerm.html.

APA

Wolfram Language. (2020). LaplacianPDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LaplacianPDETerm.html

BibTeX

@misc{reference.wolfram_2023_laplacianpdeterm, author="Wolfram Research", title="{LaplacianPDETerm}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/LaplacianPDETerm.html}", note=[Accessed: 02-October-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_laplacianpdeterm, organization={Wolfram Research}, title={LaplacianPDETerm}, year={2022}, url={https://reference.wolfram.com/language/ref/LaplacianPDETerm.html}, note=[Accessed: 02-October-2023 ]}