DerivativePDETerm

DerivativePDETerm[vars,γ]

represents a load derivative term with load derivative coefficient and model variables vars.

DerivativePDETerm[vars,γ,pars]

uses model parameters pars.

Details

  • A load derivative is typically used to model derivatives of a source or sink.
  • Computing a derivative with a source derivative coefficient 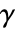is the process of adding the derivative of a source in a model by:
  • DerivativePDETerm returns a differential operators term to be used as a part of partial differential equations:
  • DerivativePDETerm can be used to model derivatives in equations with dependent variable 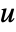, independent variables 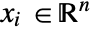and time variable .
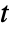  • Stationary model variables vars are vars={u[x1,…,xn],{x1,…,xn}}.
  • Time-dependent model variables vars are vars={u[t,x1,…,xn],{x1,…,xn}} or vars={u[t,x1,…,xn],t,{x1,…,xn}}.
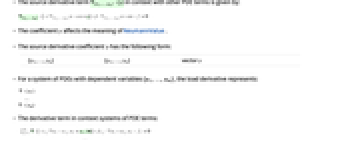
  • The source derivative term 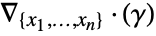in context with other PDE terms is given by:
  • The coefficient 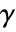affects the meaning of NeumannValue.
  • The source derivative coefficient 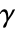has the following form:
  • {γ1,…,γn}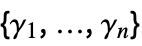{gamma_(1),...,gamma_(n)}vector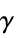
  • For a system of PDEs with dependent variables {u1,…,um}, the load derivative represents:
  • The derivative term in context systems of PDE terms:
  • The load derivative coefficient 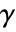is a tensor of rank 3 of the form 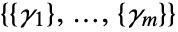where each subvector 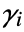is a vector of length 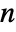that is specified in the same way as for a single dependent variable.
  • The load derivative coefficient 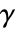can depend on time, space, parameters and the dependent variables.
  • The following parameters pars can be given:
  • parameterdefaultsymbol
    "RegionSymmetry"None
  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D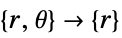
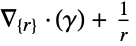
    2D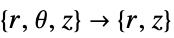
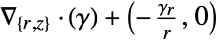
  • All quantities that do not explicitly depend on the independent variables given are taken to have zero partial derivative.

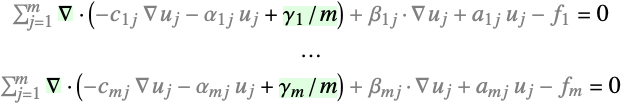
Examples

open allclose all

Basic Examples  (3)

Define a time-independent derivative term:

Activate the derivative term:

Define a time-dependent derivative term:

Solve a diffusion equation with a nonlinear derivative term and a source term:

Visualize the result:

Scope  (9)

Define a symbolic derivative term:

Define a 1D axisymmetric time-independent derivative term:

Apply Activate to the term:

Verify that the axisymmetric case is a consequence of using a truncated cylindrical coordinate system using the operators that compose the derivative term:

Define a 2D stationary derivative term:

Define a 2D axisymmetric time-independent derivative term:

Apply Activate to the term:

Verify that the axisymmetric case is a consequence of using a truncated cylindrical coordinate system using the operators that compose the derivative term:

Define a derivative with multiple dependent variables:

Define a nonlinear derivative with multiple dependent variables:

Define a nonlinear 2D axisymmetric derivative with multiple dependent variables:

The DerivativePDETerm can be used to compute the derivative of a differential equation component. Set up variables, a region and a boundary condition:

Set up a term for which the derivative is needed in the differential equation:

Solve the equation:

Solve the equation while explicitly computing the derivative of the term:

Show that the solutions are identical up to numerical precision:

Set up a system of derivative terms with DerivativePDETerm:

Wolfram Research (2020), DerivativePDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/DerivativePDETerm.html.

Text

Wolfram Research (2020), DerivativePDETerm, Wolfram Language function, https://reference.wolfram.com/language/ref/DerivativePDETerm.html.

CMS

Wolfram Language. 2020. "DerivativePDETerm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DerivativePDETerm.html.

APA

Wolfram Language. (2020). DerivativePDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DerivativePDETerm.html

BibTeX

@misc{reference.wolfram_2025_derivativepdeterm, author="Wolfram Research", title="{DerivativePDETerm}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DerivativePDETerm.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_derivativepdeterm, organization={Wolfram Research}, title={DerivativePDETerm}, year={2020}, url={https://reference.wolfram.com/language/ref/DerivativePDETerm.html}, note=[Accessed: 21-February-2025 ]}