Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

DerivativePDETerm

DerivativePDETerm[vars,γ]

表示负载导数项，其中负载导数系数为，模型变量为 vars.

DerivativePDETerm[vars,γ,pars]

使用模型参数 pars.

更多信息

负载导数通常用于模拟源或汇 (Sink) 的导数.
计算源导数系数为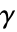的导数是在模型中添加源导数的过程，方式如下：

DerivativePDETerm 返回微分算子项，该项将用作偏微分方程的一部分：

DerivativePDETerm 可用来模拟方程导数，其中因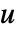变量为，自变量为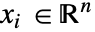，时间变量为 .
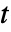平稳模拟变量 vars 为 vars={u[x₁,…,x_n],{x₁,…,x_n}}.
与时间相关的模型变量 vars 为 vars={u[t,x₁,…,x_n],{x₁,…,x_n}} 或 vars={u[t,x₁,…,x_n],t,{x₁,…,x_n}}.
与其他偏微分方程项相关的源导数项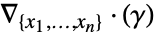由下式给出：

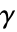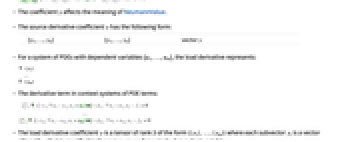
系数影响 NeumannValue 的意义.
源导数系数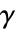具有以下形式：
{γ₁,…,γ_n} 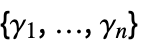${gamma_(1),...,gamma_(n)}$ 向量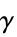
对于具有因变量 {u₁,…,u_m} 的偏微分方程组，负载导数表示：

导数项在相关的偏微分方程组中：

负载导数系数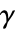是秩为 3 的张量，形如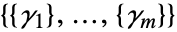，其中各子向量为长度为的向量，其指定方式与单个因变量的指定方式相同.
负载导数系数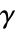可取决于时间、空间、参数和因变量.
可以给出以下参数 pars：
参数默认符号

"RegionSymmetry" None
参数 "RegionSymmetry" 的一个可能选项是 "Axisymmetric".
"Axisymmetric" 区域对称性表示截断圆柱坐标系，其中通过移除角度变量来减少圆柱坐标，如下所示：
维数化简 方程式

1D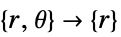

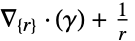
2D
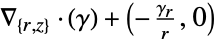
所有不明确依赖于给定自变量的量都被视为具有零偏导数.

范例

打开所有单元关闭所有单元

基本范例 (3)

定义与时间无关的导数项：

通过 Activate 激活导数项：

定义与时间相关的导数项：

求解具有非线性导数项和源项的扩散方程：

可视化结果：

范围 (9)

定义符号导数项：

定义一维轴对称非依时导数项：

将 Activate 应用于项：

使用构成导数项的算子验证轴对称情况是使用截断圆柱坐标系的结果：

定义二维平稳导数项：

定义一个二维轴对称非依时导数项：

将 Activate 应用于项：

使用构成导数项的算子验证轴对称情况是使用截断圆柱坐标系的结果：

定义具有多个因变量的导数：

定义具有多个因变量的非线性导数：

定义具有多个因变量的非线性二维轴对称导数：

DerivativePDETerm 可用于计算微分方程组件的导数. 设置变量、区域和边界条件：

设置在微分方程中需要导数的项：

解方程：

在显式计算项的导数的同时解方程：

证明解在数值精度上是相同的：

通过 DerivativePDETerm 建立导数项的系统：

顶部