DiscreteChirpZTransform[list]
gives the chirp Z transform of list.
DiscreteChirpZTransform[list,n]
returns a length n chirp Z transform.
DiscreteChirpZTransform[list,n,w]
uses a spiral path on the complex ![]() plane defined by w.
plane defined by w.
DiscreteChirpZTransform[list,n,w,a]
uses a as the complex starting point.
DiscreteChirpZTransform[list,{n1,n2,…},{w1,w2,…},{a1,a2,…}]
gives the multidimensional chirp Z transform.


DiscreteChirpZTransform
DiscreteChirpZTransform[list]
gives the chirp Z transform of list.
DiscreteChirpZTransform[list,n]
returns a length n chirp Z transform.
DiscreteChirpZTransform[list,n,w]
uses a spiral path on the complex ![]() plane defined by w.
plane defined by w.
DiscreteChirpZTransform[list,n,w,a]
uses a as the complex starting point.
DiscreteChirpZTransform[list,{n1,n2,…},{w1,w2,…},{a1,a2,…}]
gives the multidimensional chirp Z transform.
Details
- The chirp Z transform is an algorithm for evaluating the list Z transform of a finite duration sequence along a spiral path in the
 plane of the form
plane of the form  . With DiscreteChirpZTransform[list,n,w,a], the Z transform is evaluated at points
. With DiscreteChirpZTransform[list,n,w,a], the Z transform is evaluated at points  for integers
for integers 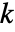 from 0 to
from 0 to  .
. - DiscreteChirpZTransform[list] is equivalent to DiscreteChirpZTransform[list,Length[list]].
- DiscreteChirpZTransform[list,n] is equivalent to DiscreteChirpZTransform[list,n,Exp[2π /n],1].
- DiscreteChirpZTransform[list] is equivalent to Fourier[list,FourierParameters->{1,-1}]. »
Examples
open all close allScope (3)
Applications (2)
Properties & Relations (4)
DiscreteChirpZTransform[list] is equivalent to Fourier[list,FourierParameters->{1,-1}]:
DiscreteChirpZTransform[list,n] is equivalent to Fourier[PadRight[list,n],FourierParameters->{1,-1}]:
DiscreteChirpZTransform[list,n] is equivalent to evaluating the Z transform of list on a circular path defined by ![]() for k from 0 to n-1:
for k from 0 to n-1:
DiscreteChirpZTransform[list,n,w,a] is equivalent to evaluating the Z transform of list on a spiral path defined by ![]() for k from 0 to n-1:
for k from 0 to n-1:
DiscreteChirpZTransform is faster compared to the explicit sampling of the Z transform:
Related Guides
History
Text
Wolfram Research (2012), DiscreteChirpZTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteChirpZTransform.html.
CMS
Wolfram Language. 2012. "DiscreteChirpZTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteChirpZTransform.html.
APA
Wolfram Language. (2012). DiscreteChirpZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteChirpZTransform.html
BibTeX
@misc{reference.wolfram_2025_discretechirpztransform, author="Wolfram Research", title="{DiscreteChirpZTransform}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteChirpZTransform.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretechirpztransform, organization={Wolfram Research}, title={DiscreteChirpZTransform}, year={2012}, url={https://reference.wolfram.com/language/ref/DiscreteChirpZTransform.html}, note=[Accessed: 11-January-2026]}