DiscreteInputOutputModel

DiscreteInputOutputModel[{g0,g1,…,gn-1},u]

represents a discrete-time model with input u and output at sampling instant i.

DiscreteInputOutputModel[{g0,g1,…,gn-1},u,y]

can be used to specify outputs that also depend on the output variables y.

DiscreteInputOutputModel[…,{{u1,{…,u10}},…},{{y1,{…,y10}},…}]

specifies input and output values for each signal for instants k<=0.

Details and Options

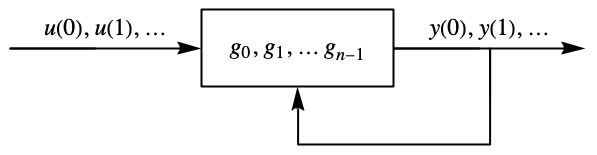
  • DiscreteInputOutputModel represents a system whose output at regularly spaced sampling instants is a function of the inputs and previous outputs of the system.
  • DiscreteInputOutputModel can be used to represent discrete-time systems in input-output form, including discrete-time TransferFunctionModel objects. It is typically used to represent the MPC controller computed in ModelPredictiveController.
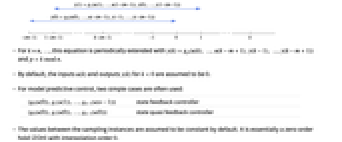
  • The input-output model represents a moving window of length m of past input and output according to 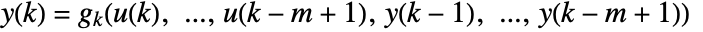, for .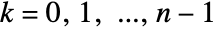
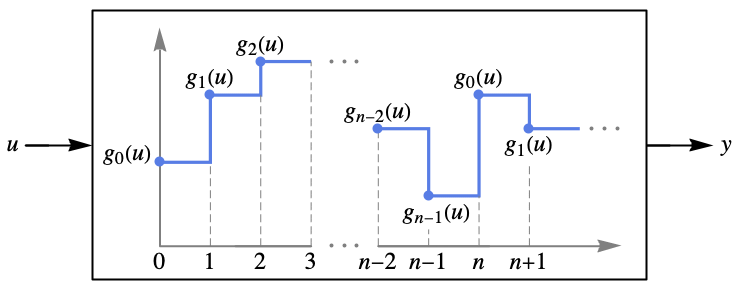
  • For k=n,…, this equation is periodically extended with 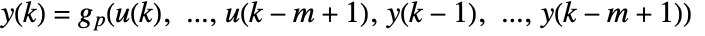and p=TemplateBox[{k, n}, Mod].
  • By default, the inputs 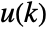and outputs 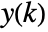for 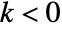are assumed to be .
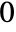  • For model predictive control, two simple cases are often used:
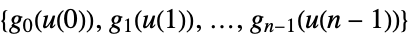
  • state feedback controller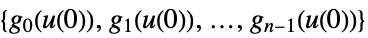
    state quasi feedback controller
  • The values between the sampling instances are assumed to be constant by default. It is essentially a zero-order hold (ZOH) with interpolation order .
  • The integer sampling instances ki and outputs 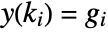can be explicitly specified as DiscreteInputOutputModel[{{k0,g0},…,{kn-1,gn-1}},…].
  • The time ti is related to the sampling instant ki by ti=τ ki, where τ is the sampling period specified as DiscreteInputOutputModel[…, SamplingPeriodτ].
  • DiscreteInputOutputModel["prop"] can be used to compute properties.
  • Properties related to the output specifications {ki,gi}:
  • "FirstInstant"first instant Min[{k0,k1,…}]
    "FirstValue"value at the first instant
    "Instants"sampling instants Sort[{k0,k1,…}]
    "LastInstant"last instant Max[{k0,k1,…}]
    "LastValue"value at the last instant
    "Path"instant-value pairs {{k0,g0},…}
    "PathComponent"first path component
    "PathComponents"all the paths split into univariate components
    "PathFunction"interpolated path function
    "PathLength"length of the path ("Horizon")
    "Values"output values {g0,g1,…}
  • Basic model properties:
  • "InputsCount"number of inputs
    "InputVariables"input variables u
    "OutputsCount"number of outputs
    "OutputVariables"output variables y
    "Type"the type of input-output relationship
    "SamplingPeriod"sampling period sp
  • Time series properties:
  • "FirstTime"time corresponding to the first instant
    "LastTime"time corresponding to the last instant
    "TemporalData"multipath TemporalData object
    "TimePath"instant-value pairs {{t0,g0},…}
    "Times"the times corresponding to the sampling instants
    "TimeSeries"TimeSeries object
    "TimeValues"the output values at the sampling times
  • DiscreteInputOutputModel takes the following options:
  • MissingDataMethod Nonemethod to use for missing values
    ResamplingMethod {"Interpolation", InterpolationOrder0}method to use for resampling paths
    SamplingPeriod Automaticsampling period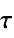

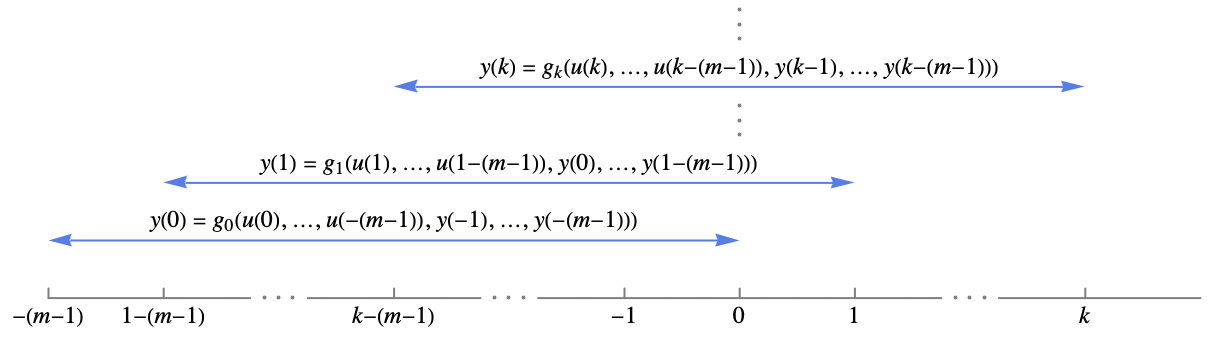
Examples

open allclose all

Basic Examples  (3)

A model whose output depends only on the input:

Its response to a random input sequence:

A model whose output depends on the input and output:

Its response to a sinusoidal input:

A model with nonzero initial conditions:

Its response to a ramp-like input sequence:

The response with zero initial conditions is different:

Scope  (30)

Basic Uses  (8)

A system whose output is the current input value:

Its output is the same as the input:

For longer input sequences, the output is computed assuming periodicity:

A system whose output is the average of the previous and current inputs:

A system whose output is the average of the previous output and current input:

A system that computes the running maximum value:

Obtain the same result using FoldList:

A multi-output system that computes the running maximum and minimum values:

Obtain the same result using FoldList:

Specify nonzero initial values:

The response to a set of negative inputs:

The response to a set of positive inputs:

The model with default zero values:

The maximum values are erroneously always 0 for negative inputs:

The minimum values are erroneously always 0 for positive inputs:

A two-output system with periodicity 3:

Its response to a ramp input:

A system with a series of piecewise outputs:

Its response to random inputs:

TransferFunctionModel  (4)

The TransferFunctionModel of a single-input single-output (SISO) system:

The equivalent DiscreteInputOutputModel:

The responses are the same:

The TransferFunctionModel of a multiple-input single-output (MISO) system:

The equivalent DiscreteInputOutputModel:

The responses are the same:

The TransferFunctionModel of a single-input multiple-output (SIMO) system:

The equivalent DiscreteInputOutputModel:

The responses are the same:

The TransferFunctionModel of a multiple-input multiple-output (MIMO) system:

The equivalent DiscreteInputOutputModel:

The responses are the same:

ModelPredictiveController  (2)

The feedback gains model of a ModelPredictiveController design:

The feedback gains are a series of piecewise functions of the states:

The quasi feedback gains model is also a DiscreteInputOutputModel:

It is a series of piecewise functions of the states at time 0:

The feedback gains model of a multi-input ModelPredictiveController design:

The values of the piecewise functions are of length 2, corresponding to the two inputs:

Properties  (16)

Obtain all the values in the model:

The first value:

The last value:

The value at a specific instant:

All the instants:

The first instant:

The last instant:

The list of instant-values pairs:

Split a multivariable path into univariate components:

The path of the first component:

The path of the second component:

"PathComponent" gives the first component:

Get the second component:

Get several components:

The interpolated path function:

The path length:

Basic model properties:

Properties specified in terms of time:

Obtain multiple properties as a list:

Obtain all properties as an Association:

Obtain all properties as a Dataset:

Options  (3)

MissingDataMethod  (1)

Specify how to handle missing values:

ResamplingMethod  (1)

The default resampling method has interpolation order 0:

Specify an interpolation order of 1:

The values with interpolation order 1:

SamplingPeriod  (1)

The default sampling period is 1:

Since the sampling instants and times coincide, "Path" and "TimePath" give the same result:

The "TimePath" can also be obtained from the "Path" of the "TimeSeries":

A system with sampling period 2:

The "Path" is in terms of sampling instants, while "TimePath" is in terms of time values:

Applications  (3)

Compute a lowpass FIR kernel:

Assemble it is as a DiscreteInputOutputModel:

Compute its response to a noisy sinusoid:

The same result can be obtained using ListConvolve:

The two responses are indeed the same:

Compute the discrete approximation of an IIR filter:

Assemble it as a DiscreteInputOutputModel:

Compute its response to a noisy sinusoidal input:

The analog TransferFunctionModel representation gives almost the same response:

Compute the feedback gains model and closed-loop system for an MPC design:

The feedback gains model is a discrete input-output model and part of the closed-loop system:

Simulate the closed-loop system:

Properties & Relations  (4)

Form a convolution:

ListConvolve gives the same result:

A linear recurrence equation:

Represent it using a DiscreteInputOutputModel:

Its response to an input sequence:

RecurrenceFilter gives the same response:

A process with a discrete TransferFunctionModel representation:

It also has a DiscreteInputOutputModel representation:

The responses are the same:

Without input and output variables, DiscreteInputOutputModel is essentially a TimeSeries:

The equivalent TimeSeries object:

Its path:

Obtain the time series as a property:

It has the same path:

The time path can also be obtained directly:

Possible Issues  (2)

Obtaining the time series could change the specification from a sampling instant to time stamps:

The value at sampling instant 1:

Compute the equivalent time series:

The time series is not in terms of the sampling instants:

Use the equivalent time stamp:

The time series path:

The time series path from the original model is the same:

However, the path of the original model is in terms of sampling instants:

The initial values and are not used in computing the response of the system:

Wolfram Research (2022), DiscreteInputOutputModel, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

Text

Wolfram Research (2022), DiscreteInputOutputModel, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

CMS

Wolfram Language. 2022. "DiscreteInputOutputModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html.

APA

Wolfram Language. (2022). DiscreteInputOutputModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html

BibTeX

@misc{reference.wolfram_2024_discreteinputoutputmodel, author="Wolfram Research", title="{DiscreteInputOutputModel}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discreteinputoutputmodel, organization={Wolfram Research}, title={DiscreteInputOutputModel}, year={2022}, url={https://reference.wolfram.com/language/ref/DiscreteInputOutputModel.html}, note=[Accessed: 21-November-2024 ]}