EulerAngles

EulerAngles[r]

回転行列 r に対応するオイラー角{α,β,γ}を与える．

EulerAngles[r,{a,b,c}]

回転順序が{a,b,c}のオイラー角{α,β,γ}を与える．

詳細

  • EulerAngles[r,{a,b,c}]は，EulerMatrix[{α,β,γ},{a,b,c}]r となるような角{α,β,γ}を与える．
  • EulerAngles[r]は，z-y-z回転EulerAngles[r,{3,2,3}]に等しい．
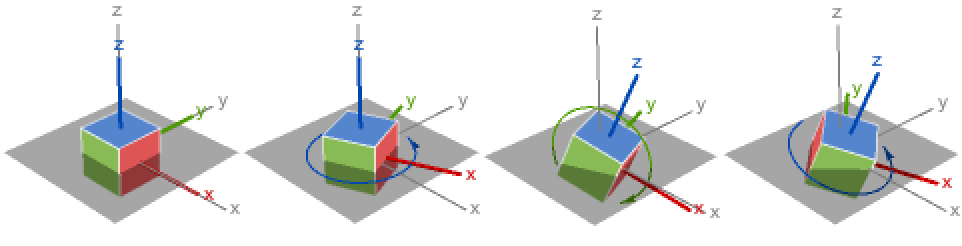
  • デフォルトのz-y-z角EulerAngles[r,{3,2,3}]は，回転を3段階に分解する．
  • 回転軸 a，b，c は，任意の整数1，2あるいは3でよい．しかし，任意の3D回転を指定するのに十分に一般的である組合せは12しかない．
  • 最初と最後の軸が繰り返される回転
  • {3,2,3}z-y-z回転（デフォルト）
    {3,1,3}z-x-z回転
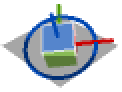
    {2,3,2}y-z-y回転
    {2,1,2}y-x-y 回転
    {1,3,1}x-z-x回転
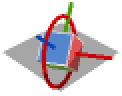
    {1,2,1}x-y-x回転
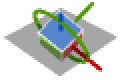
  • 3軸がみな違う回転
  • {1,2,3}x-y-z回転
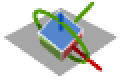
    {1,3,2}x-z-y回転
    {2,1,3}y-x-z回転
    {2,3,1}y-z-x回転
    {3,1,2}z-x-y回転
    {3,2,1}z-y-x回転
  • 続く軸が繰り返される回転は，3Dにおける可能なすべての回転を表すことができないので，可逆ではない．

例題

すべて開くすべて閉じる

例  (2)

回転行列からオイラー角を得る：

指定された回転順の回転行列からオイラー角を得る：

アプリケーション  (6)

回転表現  (4)

オイラー角を1つの回転順から別の回転順に変換する：

ロールピッチヨー角をオイラー角に変換する：

t{1,1,1} + s{1,–2,1}で与えられる平面上の3D回転のためのオイラー角を得る：

オイラー回転の組み合せから，オイラー角の単一集合を求める：

どちらも同じ変換（赤）を行う：

座標系  (2)

とをお互いから回転している直交座標の座標軸とする：

TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose]=R.TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose]（回転された 軸は で与えられる等）のとき，TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose]は直交行列でその逆行列はその置換であるので，R=TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose].{x_1,y_1,z_1}である：

が座標系を関連付ける回転であることを確かめる：

を定義する，対応するオイラー角を求める：

可視化する：

右手系のZ-Up座標系は，数学の直交座標で一般的である．しかし，コンピュータグラフィックスのアプリケーションでは，右手系のY-Up座標系のような別の系が使われることがある．前の例を使ってZ-UpをY-Up座標系に変換するオイラー角を求める：

回転行列 と， を定義する対応するオイラー角を求める：

これらの角を使ってY-Up座標系を変換し可視化する（Z-Up系，Y-Up系，変換されたY-Up系）：

特性と関係  (1)

EulerAnglesは，EulerMatrixがそれについて同じ回転行列与える角を与える：

角度は等しくなくてもよい：

しかし，両方の角度集合は同じ回転行列を生成する：

考えられる問題  (1)

EulerMatrixを使うと等しい軸の連続が許容され，これが回転行列を生成する：

しかし，EulerAnglesでは連続する軸が異なっていなければならない：

これは，連続する軸が等しいと表すことができない回転行列が出てくるからである：

Wolfram Research (2015), EulerAngles, Wolfram言語関数， https://reference.wolfram.com/language/ref/EulerAngles.html.

テキスト

Wolfram Research (2015), EulerAngles, Wolfram言語関数， https://reference.wolfram.com/language/ref/EulerAngles.html.

CMS

Wolfram Language. 2015. "EulerAngles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EulerAngles.html.

APA

Wolfram Language. (2015). EulerAngles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerAngles.html

BibTeX

@misc{reference.wolfram_2024_eulerangles, author="Wolfram Research", title="{EulerAngles}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EulerAngles.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eulerangles, organization={Wolfram Research}, title={EulerAngles}, year={2015}, url={https://reference.wolfram.com/language/ref/EulerAngles.html}, note=[Accessed: 21-November-2024 ]}