EulerAngles

EulerAngles[r]

给出对应于旋转矩阵 r 的欧拉角 {α,β,γ}.

EulerAngles[r,{a,b,c}]

给出旋转顺序为 {a,b,c} 的欧拉角 {α,β,γ}.

更多信息

  • EulerAngles[r,{a,b,c}] 给出角 {α,β,γ}，满足 EulerMatrix[{α,β,γ},{a,b,c}]r.
  • EulerAngles[r] 等价于 EulerAngles[r,{3,2,3}]，z-y-z 旋转.
  • 默认 z-y-z 角 EulerAngles[r,{3,2,3}] 将旋转分解为三个步骤：
  • 旋转轴 a、b 和 c 可以是任意整数 1、2 或者 3. 但是，只有十二个组合足够普适可以指定任意三维旋转.
  • 第一个轴和最后一个轴重复的旋转：
  • {3,2,3}z-y-z 旋转（默认）
    {3,1,3}z-x-z 旋转
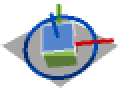
    {2,3,2}y-z-y 旋转
    {2,1,2}y-x-y 旋转
    {1,3,1}x-z-x 旋转
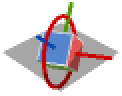
    {1,2,1}x-y-x 旋转
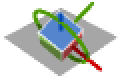
  • 所有三个轴不同的旋转：
  • {1,2,3}x-y-z 旋转
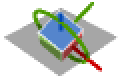
    {1,3,2}x-z-y 旋转
    {2,1,3}y-x-z 旋转
    {2,3,1}y-z-x 旋转
    {3,1,2}z-x-y 旋转
    {3,2,1}z-y-x 旋转
  • 重复其余的轴的旋转可能不可逆，因为这些不能表示在三维空间中的所有旋转.

范例

打开所有单元关闭所有单元

基本范例  (2)

从旋转矩阵获取欧拉角：

从具有给定旋转顺序的旋转矩阵获取欧拉角：

应用  (6)

旋转表示  (4)

将欧拉角从一个旋转顺序转化为另一个顺序：

将滚动-俯仰-水平角转化为欧拉角：

在由 t{1,1,1} + s{1,–2,1} 给定的平面中获得三维旋转的欧拉角：

从欧拉旋转组合求欧拉角的单个集合：

两者执行相同的变换（红色）：

坐标系  (2)

令 和 为两个互相旋转的正交坐标系的坐标轴：

给定 TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose]=R.TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose]，其中旋转 轴由 给出，即可发现 R=TemplateBox[{{{, {{x, _, 2}, ,, {y, _, 2}, ,, {z, _, 2}}, }}}, Transpose].{x_1,y_1,z_1}，因为 TemplateBox[{{{, {{x, _, 1}, ,, {y, _, 1}, ,, {z, _, 1}}, }}}, Transpose] 是正交矩阵，而它的逆是它的转置：

验证 是与坐标系相关的旋转：

求定义 的相应欧拉角：

可视化：

右手系、z 轴向上的坐标系是数学中笛卡尔坐标的标准. 但是，在计算机图形应用中，可能采用不同的系统，比如右手系、y 轴向上的系统. 使用前面的例子，求将 z 轴向上的坐标系变换为 y 轴向上坐标系：

获得旋转矩阵 和定义 的相应欧拉角：

使用这些角变换 y 轴向上坐标系，并且可视化（z 轴向上系统、y 轴向上系统和变换过的 y 轴向上系统）：

属性和关系  (1)

EulerAngles 返回角度，其中 EulerMatrix 给出相同旋转矩阵：

角度不必相等：

但是，两个角度集合产生相等旋转矩阵：

可能存在的问题  (1)

EulerAngles 允许相等的相邻轴，并且这能产生一个旋转矩阵：

但是，EulerAngles 要求相邻轴是不同的：

这是因为相邻轴是相等的话，无法表示某些旋转矩阵：

Wolfram Research (2015)，EulerAngles，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerAngles.html.

文本

Wolfram Research (2015)，EulerAngles，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerAngles.html.

CMS

Wolfram 语言. 2015. "EulerAngles." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EulerAngles.html.

APA

Wolfram 语言. (2015). EulerAngles. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EulerAngles.html 年

BibTeX

@misc{reference.wolfram_2024_eulerangles, author="Wolfram Research", title="{EulerAngles}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EulerAngles.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eulerangles, organization={Wolfram Research}, title={EulerAngles}, year={2015}, url={https://reference.wolfram.com/language/ref/EulerAngles.html}, note=[Accessed: 21-November-2024 ]}