FeedbackLinearize
FeedbackLinearize[asys]
输入-输出通过状态变换和反馈线性化 AffineStateSpaceModel asys.
FeedbackLinearize[asys,{z,v}]
指明新状态 z 和新的控制输入 v.
FeedbackLinearize[asys,{z,v},"prop"]
计算属性 "prop".
更多信息和选项




- FeedbackLinearize 也叫做精确线性化.
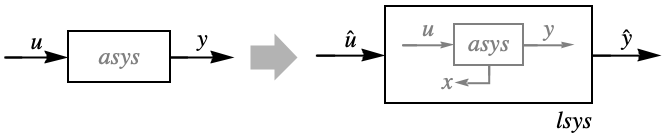
- FeedbackLinearize 将从非线性系统 asys 中构建线性系统 lsys,这样就可以用对线性系统 lsys 的线性控制设计技巧来控制非线性系统 asys.
- FeedbackLinearize 返回一个可用于提取基于反馈线性化分析和设计需求的属性的 LinearizingTransformationData 对象.
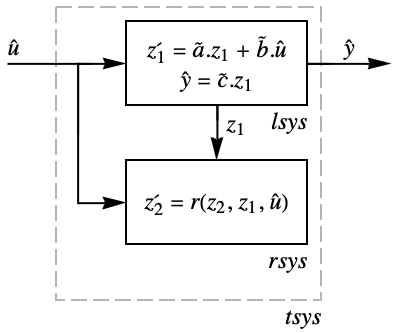
- 已变换系统 tsys 包含一个线性系统 lsys 和可能的一个需要稳定的有内部动力的剩余数系统 rsys,否则不可观测.
- 与已变换系统相关的属性包括:
-
"LinearSystem" 系统模型 lsys "ResidualSystem" 系统模型 rsys "TransformedSystem" 系统模型 tsys - 如果剩余数系统 rsys 是稳定的,通过设计一个对 lsys 的稳定控制器 cs 得到的闭环系统将是稳定的.
- 为了部署对原非线性系统 asys 的控制器,需要变换控制器 cs 来使用原始变量.
- 与原始坐标的控制器和估计器的变换相关的属性:
-
{"OriginalSystemController",cs} 原始坐标系中的控制器 cs {"OriginalSystemEstimator",es} 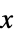 和
和 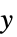 的估计器
的估计器{"ClosedLoopSystem",cs} 原始坐标系中的闭环系统 {"OriginalSystemFullController",cs} 原始坐标系中 cs 的系统模型 - 反馈线性化更细致的属性也是可用的, 这些属性可用于部署可选择的控制器、估计器等的模拟和实现.
- 系统 asys
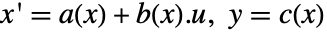 与反馈补偿器、前置补偿器和后置补偿器相连接来给出一个修正系统
与反馈补偿器、前置补偿器和后置补偿器相连接来给出一个修正系统 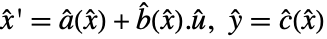 ,其中 where
,其中 where 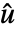 是修正输入、
是修正输入、 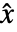 是由
是由  和可能额外补偿状态构成的状态向量而
和可能额外补偿状态构成的状态向量而  是修正输出.
是修正输出. - 反馈补偿器本质上是由
 给出的
给出的 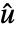 和
和 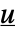 之间的转换,其中
之间的转换,其中  是去耦矩阵.
是去耦矩阵. - 补偿器属性包括:
-
"FeedbackCompensator" 从 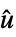 到
到  的系统模型
的系统模型"InverseFeedbackCompensator" 从 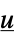 到
到  的系统模型
的系统模型"InverseFeedbackTransformation" 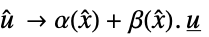 规则列表
规则列表"DecouplingMatrix" 矩阵 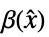
"PreCompensator" 从 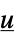 到
到 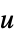 的系统模型
的系统模型"PostCompensator" 从 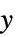 到
到 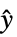 的系统模型
的系统模型 - 为了得到一个显性线性系统 lsys 和可能的剩余数系统 rsys,需要执行一个状态变换
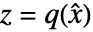 .
. - 与状态变换和零动态相关的属性包括:
-
"InverseStateTransformation"  规则列表
规则列表"ZeroDynamicsSystem" 系统模型 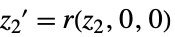
"ZeroDynamicsManifold" rsys 状态演变上的增多 - FeedbackLinearize 采用有如下设置的 Method 选项:
-
Automatic 自动裁决方法(默认) "Identity" 应用有恒等变换的恒等反馈 "Burnovsky" 以 Burnovsky 形式返回 lsys

范例
打开所有单元关闭所有单元范围 (21)
基本用法 (5)
控制器与估计器属性 (5)
补偿器属性 (5)
选项 (2)
应用 (8)
机电系统 (2)
设计一个控制器,使用精确线性化使磁悬浮系统稳定,并与基于近似线性化的设计比较:
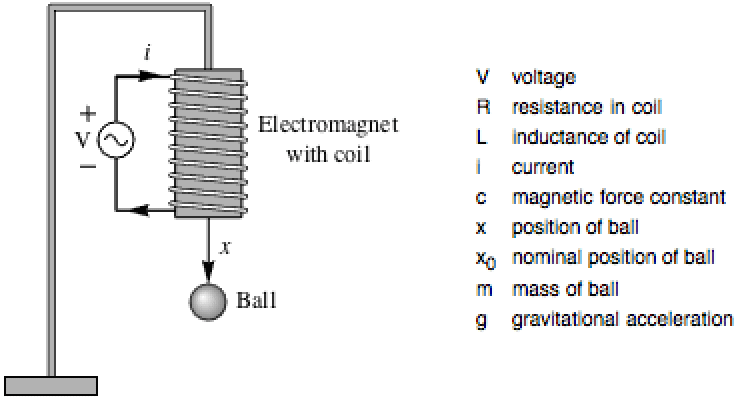
无反馈的系统是不稳定的,在这里初始值为 {0.2,0.,0.1}:
找到一个两轮倒立摆(例如赛格威)的稳定控制器,用施加到两个直流车轮马达上的电压作为输入:

系统的 AffineStateSpaceModel 有 {θ,θ',ψ,ψ',ϕ,ϕ'} 状态:
机械系统 (2)
化学系统 (2)
电气系统 (2)
文本
Wolfram Research (2014),FeedbackLinearize,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FeedbackLinearize.html.
CMS
Wolfram 语言. 2014. "FeedbackLinearize." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FeedbackLinearize.html.
APA
Wolfram 语言. (2014). FeedbackLinearize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FeedbackLinearize.html 年