FindFundamentalCycles
finds fundamental cycles of the graph g.
Details and Options

- FindFundamentalCycles is also known as cycle basis.
- FindFundamentalCycles returns a list of cycles consisting of fundamental cycles {c1,c2,…}.
- For an undirected graph g with a spanning tree s, fundamental cycles ci are cycles that contain exactly one non-tree edge each.
- Cycles ci can be combined into new cycles by adding their edges modulo two, i.e. if the same edge is covered an odd number of times it is kept and otherwise discarded.
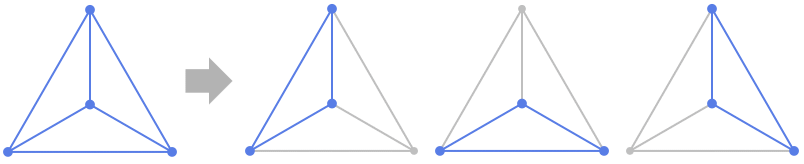
Background & Context
- FindFundamentalCycles returns a list of fundamental cycles of a graph. Here, fundamental cycles are a set of cycles that form a fundamental cycle basis, which is a set of cycles that can generate every cycle in a graph by a linear combination of members based on a spanning tree. The cycles are returned as a list of edge lists. Cycle bases are useful in the study of chemical graphs, to generate large cycle families, and to compute voltage or current in a circuit.
- FindFundamentalCycles uses the result of FindSpanningTree as the default spanning tree.
- A list of all cycles of a graph (not just the fundamental ones) may be returned using FindCycle. FindHamiltonianCycle and FindEulerianCycle return other specific types of graph cycles. EdgeCycleMatrix is a related function that can be used to return an edge cycle matrix of a graph.
Examples
open allclose allScope (2)
Wolfram Research (2014), FindFundamentalCycles, Wolfram Language function, https://reference.wolfram.com/language/ref/FindFundamentalCycles.html.
Text
Wolfram Research (2014), FindFundamentalCycles, Wolfram Language function, https://reference.wolfram.com/language/ref/FindFundamentalCycles.html.
CMS
Wolfram Language. 2014. "FindFundamentalCycles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindFundamentalCycles.html.
APA
Wolfram Language. (2014). FindFundamentalCycles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindFundamentalCycles.html