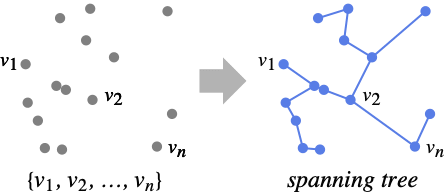
FindSpanningTree[{v1,v2,…,vn}]
finds a spanning tree that minimizes the total distance between the vi.
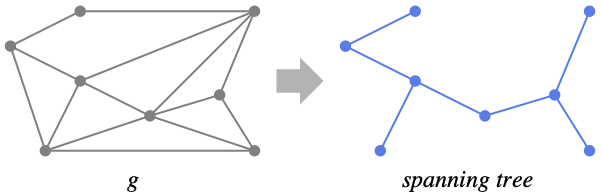
finds a spanning tree of the graph g that minimizes the total distances between vertices.
FindSpanningTree[{g,v},…]
finds a spanning tree of the connected component of g that includes the vertex v.
FindSpanningTree[{vw,…},…]
uses rules vw to specify the graph g.


FindSpanningTree
FindSpanningTree[{v1,v2,…,vn}]
finds a spanning tree that minimizes the total distance between the vi.
finds a spanning tree of the graph g that minimizes the total distances between vertices.
FindSpanningTree[{g,v},…]
finds a spanning tree of the connected component of g that includes the vertex v.
FindSpanningTree[{vw,…},…]
uses rules vw to specify the graph g.
Details and Options


- FindSpanningTree is also known as minimum spanning tree and spanning forest.
- Typically used to find optimal connections without cycles.
- FindSpanningTree[{v1,…,vn}] gives a spanning tree of the complete graph with vertices v1,…,vn that minimizes the total distance between the vi.
- A spanning tree of a connected graph g is a subgraph of g that is a tree and connects all vertices of g.
- For weighted graphs, FindSpanningTree gives a spanning tree with minimum sum of edge weights.
- For disconnected graphs, FindSpanningTree gives a subgraph that consists of a spanning tree for each of its connected components.
- FindSpanningTree has the same options as Graph, with the following additions and changes: [List of all options]
-
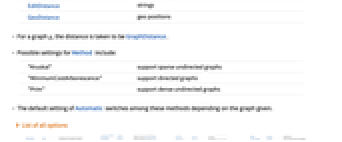
DistanceFunction Automatic function to apply to pairs of objects Method Automatic method to use - The Automatic setting for DistanceFunction includes the following choices:
-
EuclideanDistance numbers of lists of numbers EditDistance strings GeoDistance geo positions - For a graph g, the distance is taken to be GraphDistance.
- Possible settings for Method include:
-
"Kruskal" support sparse undirected graphs "MinimumCostArborescence" support directed graphs "Prim" support dense undirected graphs - The default setting of Automatic switches among these methods depending on the graph given.
-
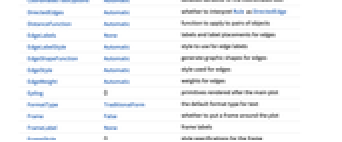
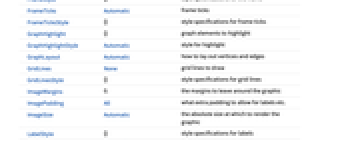
AlignmentPoint Center the default point in the graphic to align with AnnotationRules {} annotations for graph, edges and vertices AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DirectedEdges Automatic whether to interpret Rule as DirectedEdge DistanceFunction Automatic function to apply to pairs of objects EdgeLabels None labels and label placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic style used for edges EdgeWeight Automatic weights for edges Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GraphHighlight {} graph elements to highlight GraphHighlightStyle Automatic style for highlight GraphLayout Automatic how to lay out vertices and edges GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Method Automatic method to use PerformanceGoal Automatic aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotTheme $PlotTheme overall theme for the graph PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Medium size of vertices VertexStyle Automatic styles for vertices VertexWeight Automatic weights for vertices
List of all options
Examples
open all close allScope (10)
FindSpanningTree works with a list of points:
FindSpanningTree works with undirected graphs:
Find a minimum spanning tree with a start root:
Use rules to specify the graph:
FindSpanningTree works with large graphs:
Options (5)
EdgeWeight (1)
By default, the edge weight is taken to be its EdgeWeight annotation if available, and otherwise 1:
Use EdgeWeight->weights to set the edge weight:
Applications (7)
A company is planning a fiber network for a number of Chicago suburbs. It only has the right of way for its fiber along certain corridors. Some of those corridors might be more expensive. Find the subgraph of connection corridors that connect every suburb with the lowest total cost:
The phone company task is to provide phone lines to a village with 10 houses. Each node is a house and each house has a location. Find a way to wire up all houses using the least telephone wiring:
The resulting total length for the phone lines:
A two-dimensional array such that the rows have similar entries and differ only at a few places. ![]() denotes the number of different entries in row
denotes the number of different entries in row ![]() and
and ![]() . The array can be stored by representing one full row and all other rows as the entries that differ from another row. Each matrix row can be modeled as a vertex, with an edge to every other and a weight of
. The array can be stored by representing one full row and all other rows as the entries that differ from another row. Each matrix row can be modeled as a vertex, with an edge to every other and a weight of ![]() that represents the number of entries that differ. Use a minimal-weight spanning tree to find an efficient storage scheme:
that represents the number of entries that differ. Use a minimal-weight spanning tree to find an efficient storage scheme:
Store row 1 completely, and for the remaining rows store only the positions and entries where the row differs from its parent:
Build an interstate highway system joining the geographical centers of all African countries:
Minimize the total distances between all countries:
Generate mazes from a grid graph with random weights:
Find the expected size of minimal spanning trees for complete graphs with uniform random weights:
Size of a spanning tree is given as a sum of edge weights for the spanning tree:
For large complete graphs, the expected size approaches ![]() :
:
Properties & Relations (2)
The spanning tree graph is a tree:
BreadthFirstScan can be used to find a spanning tree of a graph:
Find a spanning tree using DepthFirstScan:
Possible Issues (1)
Text
Wolfram Research (2014), FindSpanningTree, Wolfram Language function, https://reference.wolfram.com/language/ref/FindSpanningTree.html (updated 2021).
CMS
Wolfram Language. 2014. "FindSpanningTree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/FindSpanningTree.html.
APA
Wolfram Language. (2014). FindSpanningTree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindSpanningTree.html
BibTeX
@misc{reference.wolfram_2025_findspanningtree, author="Wolfram Research", title="{FindSpanningTree}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/FindSpanningTree.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_findspanningtree, organization={Wolfram Research}, title={FindSpanningTree}, year={2021}, url={https://reference.wolfram.com/language/ref/FindSpanningTree.html}, note=[Accessed: 09-March-2026]}