FindShortestTour

FindShortestTour[{v1,v2,…}]

尝试找到 vi 的一种排序，使得访问所有 vi 一次的总距离最短.

FindShortestTour[graph]

尝试找到 graph 中顶点的的一种排序，使得访问每个顶点一次的总长度最短.

FindShortestTour[{v1,v2,…},j,k]

找到一个 vi 的排序，使得从 vj 到 vk 的总距离最小.

FindShortestTour[graph,s,t]

找到一个顶点的排序，使得从 s 到 t 的路径的总长度最小.

FindShortestTour[{vw,…},…]

使用规则 vw 指定图 g.

FindShortestTour[dataprop,…]

给出了 data 的属性 prop.

更多信息和选项

  • FindShortestTour 又称作旅行推销员问题（TSP）.
  • FindShortestTour 返回形如 {dmin,{vi1,vi2,…}} 的列表，其中 dmin 是求得的路径的长度，而 {vi1,vi2,…} 是排序.
  • 在 FindShortestTour[dataprop,…] 中，prop 的可能形式包括：
  • "Elements"最短路径的元素
    "Indices"最短路径的索引
    "Length"最短路径的距离
    {prop1,prop2,…}多种形式列表
    All元素、索引和距离的关联
  • 可以给出下列选项：
  • DistanceFunction Automatic应用于对象对的函数
    MethodAutomatic使用的方法
  • DistanceFunction 基于 vi 的自动设置包括：
  • EuclideanDistance数值列表的个数
    EditDistance字符串
    GeoDistance地理位置
  • 对于 graph，距离被取为 GraphDistance，这是未加权图的最短路径长度，或者加权图的权值总和.

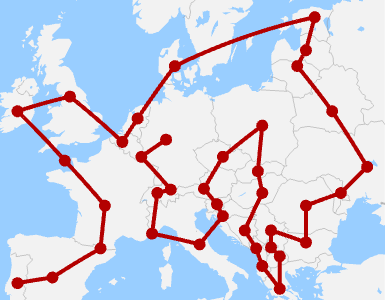
范例

打开所有单元关闭所有单元

基本范例  (3)

求平面上经过各点的最短路径长度及各点排序：

根据得到的路径对点排序：

绘制路径：

求图的最短路径：

突出显示路径：

找到在欧洲从阿尔巴尼亚到西班牙的最短路线：

显示这条路线：

范围  (7)

FindShortestTour 适用于点列表：

字符串列表：

大地测量位置的列表：

无向图：

加权图：

使用规则指定图：

FindShortestTour 作用于大规模图：

选项  (3)

DistanceFunction  (3)

在默认情况下，EditDistance 用于字符串：

这里找到经过100个点的最短路径，其中对过“河”会有相应的“惩罚”：

绘制路径，“河”用红色标出：

这里定义一个六个点上的稀疏距离矩阵，并求得最短路径：

下面用红色绘出最短路径，以及在各边上的距离：

应用  (3)

求访问平面上随机点的最短路径：

显示路线：

在三维空间上访问随机点的最短路径：

求解欧洲旅行推销员的最短路径：

地理中心的纬度和经度：

显示路线：

将达芬奇的蒙娜丽莎以连续线段形式画出：

将图像转化成点图：

画出蒙娜丽莎：

属性和关系  (2)

FindShortestTour 对于非哈密顿图给出空列表：

一个没有最短路线的图可能有一个通过所有顶点的最短路径：

可能存在的问题  (2)

对大数据集， FindShortestTour 找出至少其长度与最小值相近的路径：

用 PerformanceGoal->"Quality" 找出最优结果：

在 FindShortestTour 中，将规则视为无向边：

巧妙范例  (1)

设计一个游遍世界各国的旅行路线：

使用方位投影可视化该路线：

在地球上可视化路线：

Wolfram Research (2007)，FindShortestTour，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindShortestTour.html （更新于 2024 年）.

文本

Wolfram Research (2007)，FindShortestTour，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindShortestTour.html （更新于 2024 年）.

CMS

Wolfram 语言. 2007. "FindShortestTour." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FindShortestTour.html.

APA

Wolfram 语言. (2007). FindShortestTour. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindShortestTour.html 年

BibTeX

@misc{reference.wolfram_2024_findshortesttour, author="Wolfram Research", title="{FindShortestTour}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FindShortestTour.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findshortesttour, organization={Wolfram Research}, title={FindShortestTour}, year={2024}, url={https://reference.wolfram.com/language/ref/FindShortestTour.html}, note=[Accessed: 21-November-2024 ]}