FischerGroupFi24Prime

FischerGroupFi24Prime[]

散在型単純フィッシャー(Fischer)群を表す．

詳細

FischerGroupFi24Prime[]の置換表現は実装されていない．

予備知識

FischerGroupFi24Prime[]は，位数がであるフィッシャー群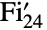を表す．この群は，位数が有限である26の散在型単純群の一つである．
フィッシャー群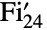は3番目に大きい散在型有限単純群である．この群は1970年代にBernd Fischerによって導入され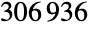，の頂点を持つグラフの3転置に対応する位数3の動作によって最初に定義された．点固定群としてフィッシャー群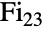を持つデフォルトの置換表現に加え，FischerGroupFi24Primeは体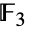上に2元の次元781の既約表現を持ち，モンスター群の位数3の元を中心化する有限被覆を持つ．フィッシャー群は，他の散在型単純群とともに，有限単純群の重要（かつ完全）な分類に大きく貢献した．
FischerGroupFi24Prime[]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．しかし，FischerGroupFi24Prime[]は置換群ではあるが，位数が大きいために，明示的な置換表現の直接的な実装は非現実的である．結果として，そのような群論関数の数多くは適用されても未評価で返されることがある．フィッシャー群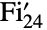の数多くの計算済みの特性を，FiniteGroupData[{"Fisher",24},"prop"]を介して得ることができる．
FischerGroupFi24Primeは他の数多くのシンボルに関連している．FischerGroupFi24Primeは集合的に散在型有限単純群の「第三世代」と呼ばれる8つの群の一つである（他にFischerGroupFi22，FischerGroupFi23，HeldGroupHe，HaradaNortonGroupHN，ThompsonGroupTh，BabyMonsterGroupB，MonsterGroupMがある）．この群は，そのすべてがモンスター群のいわゆる部分商として現れる，「Happy」な20個の散在群の一つでもある．